- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку Понятие многогранника. Призма.
Содержание
- 1. Презентация к уроку Понятие многогранника. Призма.
- 2. Многоугольником называется плоская фигура, ограниченная
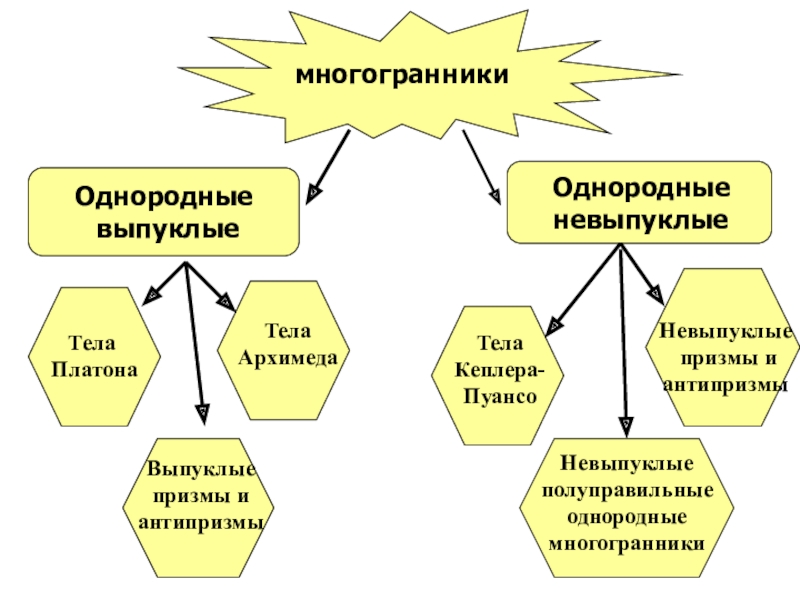
- 3. Однородные выпуклые
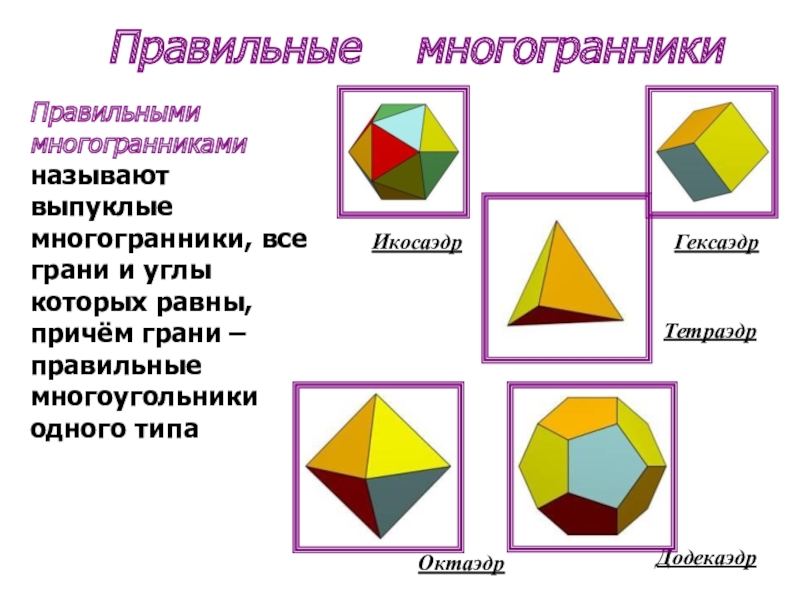
- 4. Правильные многогранники ТетраэдрГексаэдрИкосаэдрОктаэдрДодекаэдрПравильными многогранниками называют
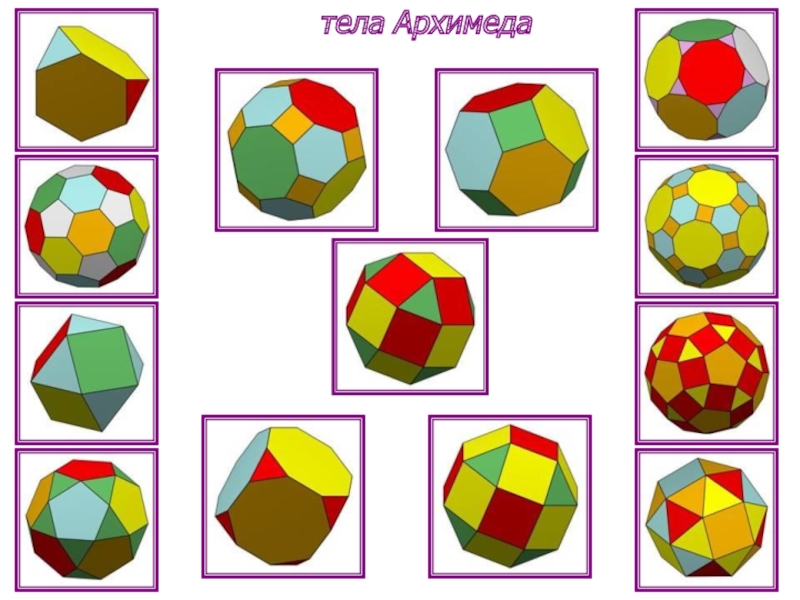
- 5. Архимедовыми телами называют выпуклые многогранники, все многогранные
- 6. тела Архимеда
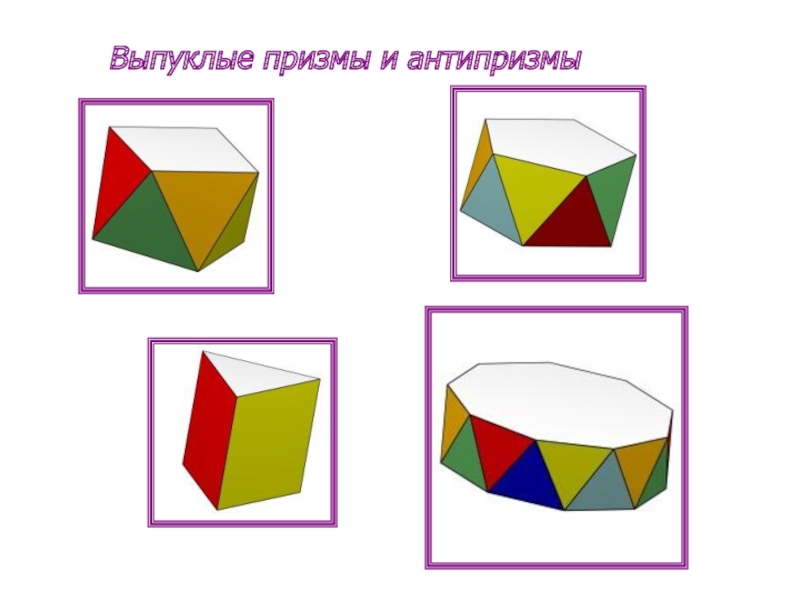
- 7. Выпуклые призмы и антипризмы
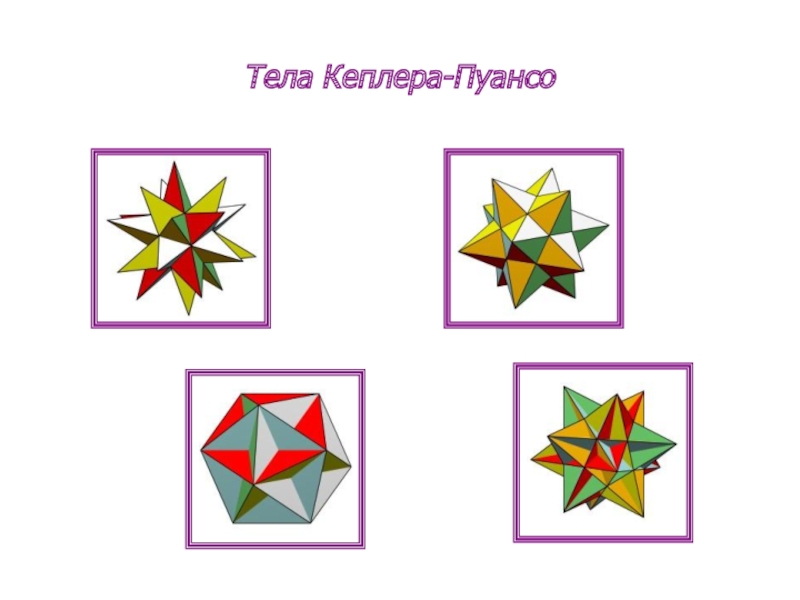
- 8. Тела Кеплера-Пуансо
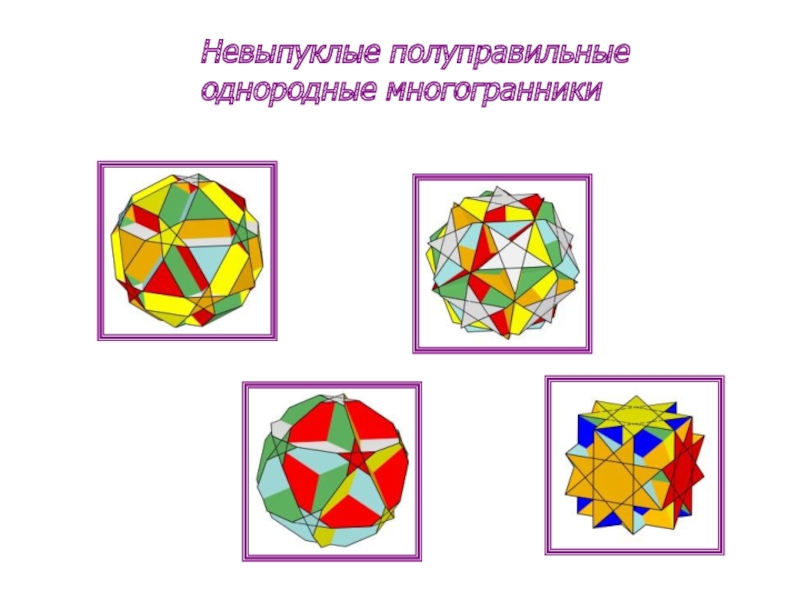
- 9. Невыпуклые полуправильные однородные многогранники
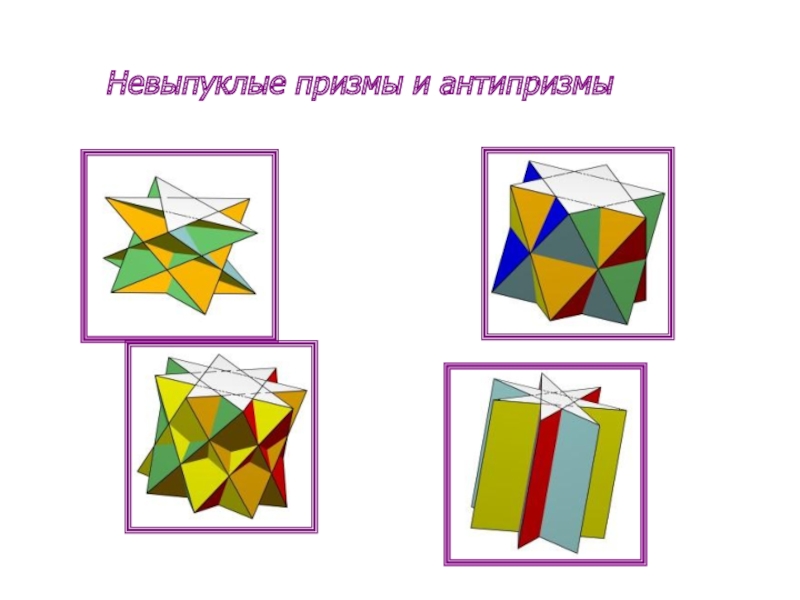
- 10. Невыпуклые призмы и антипризмы
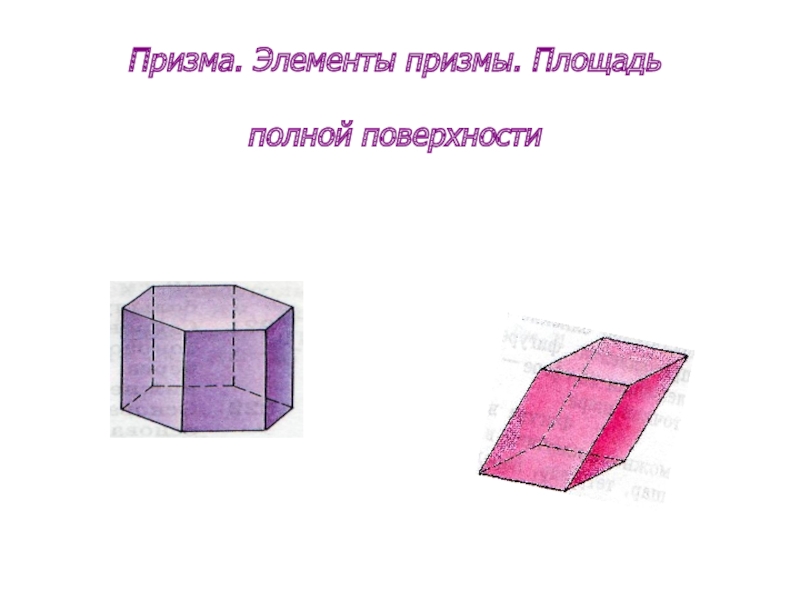
- 11. Призма. Элементы призмы. Площадь полной поверхности
- 12. Призмой называется многогранник, у которого две грани
- 13. МногогранникМногогранник, поверхность которого состоит из двух равных
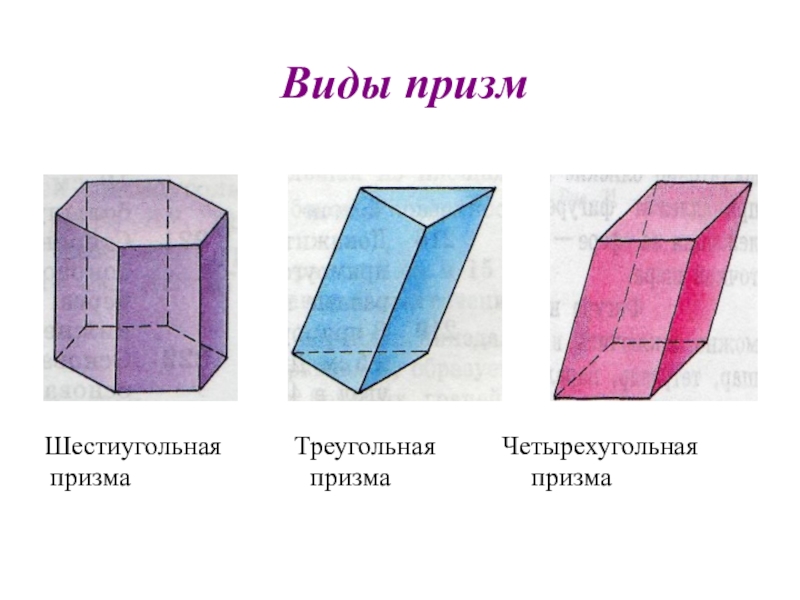
- 14. Виды призм Шестиугольная
- 15. Наклонная и прямая призма Если
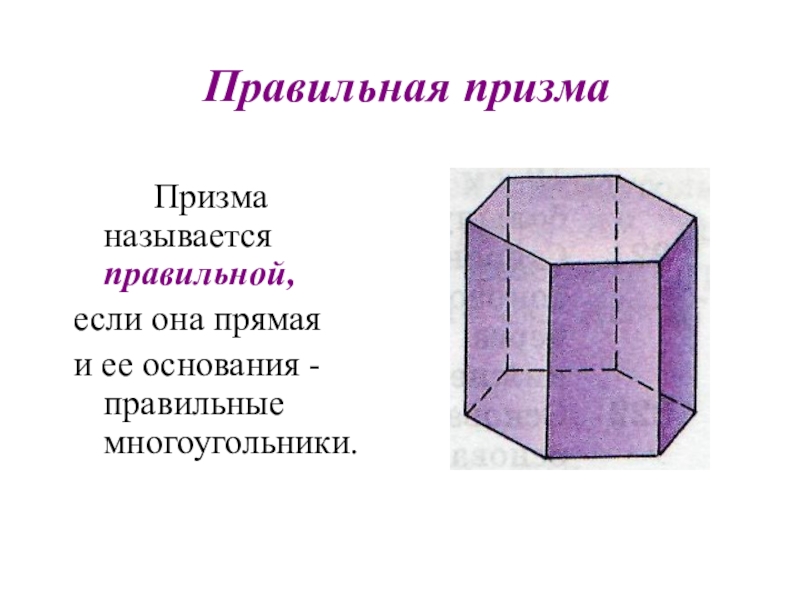
- 16. Правильная призма Призма называется правильной, если она прямая и ее основания - правильные многоугольники.
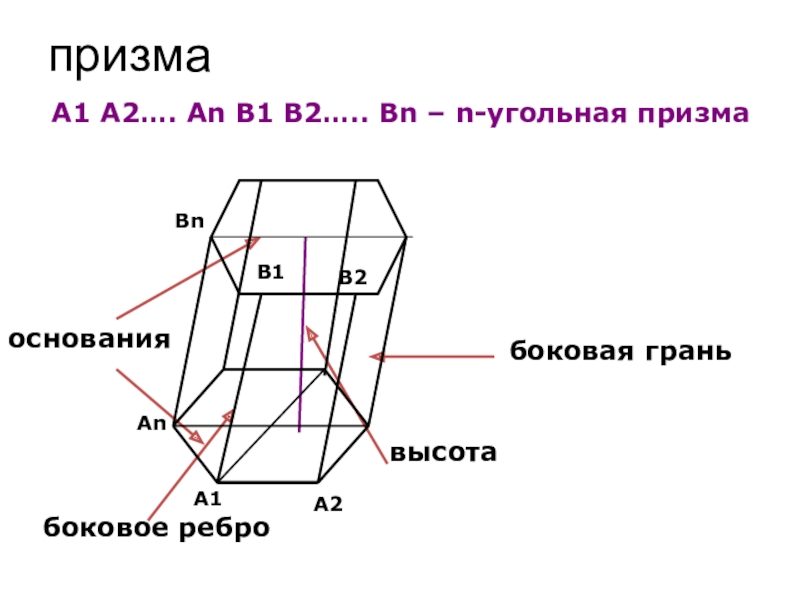
- 17. призмаоснованиябоковая граньвысотабоковое реброA1AnA2В1ВnВ2A1 A2…. An В1 В2….. Вn – n-угольная призма
- 18. Свойства призмы. 1. Основания призмы являются равными многоугольниками.2. Боковые
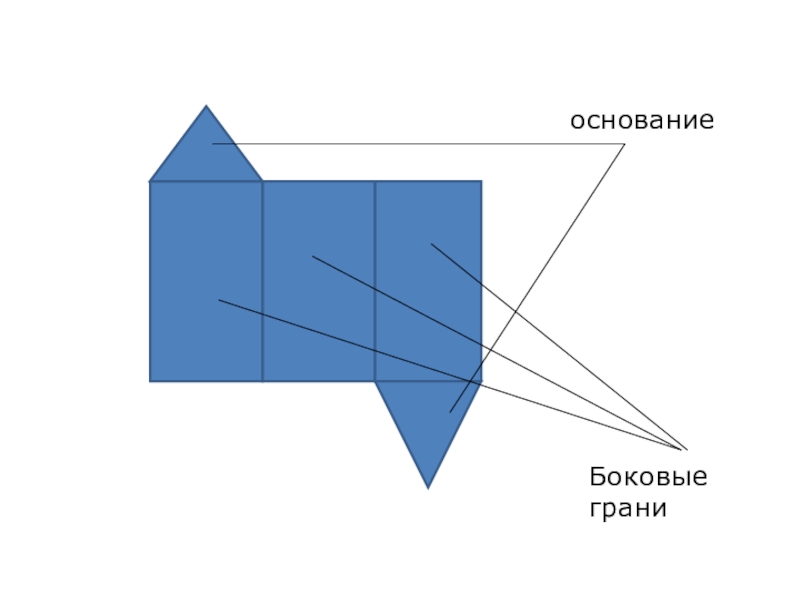
- 19. основаниеБоковые грани
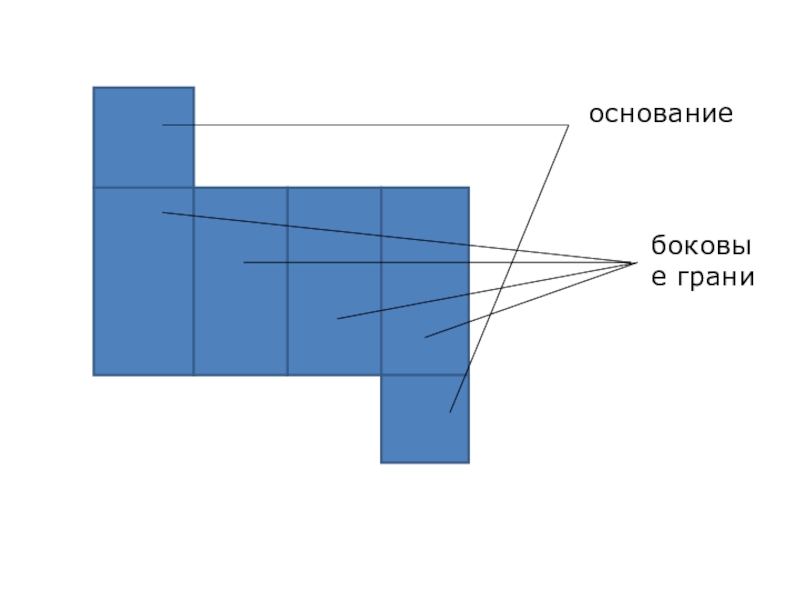
- 20. основаниебоковые грани
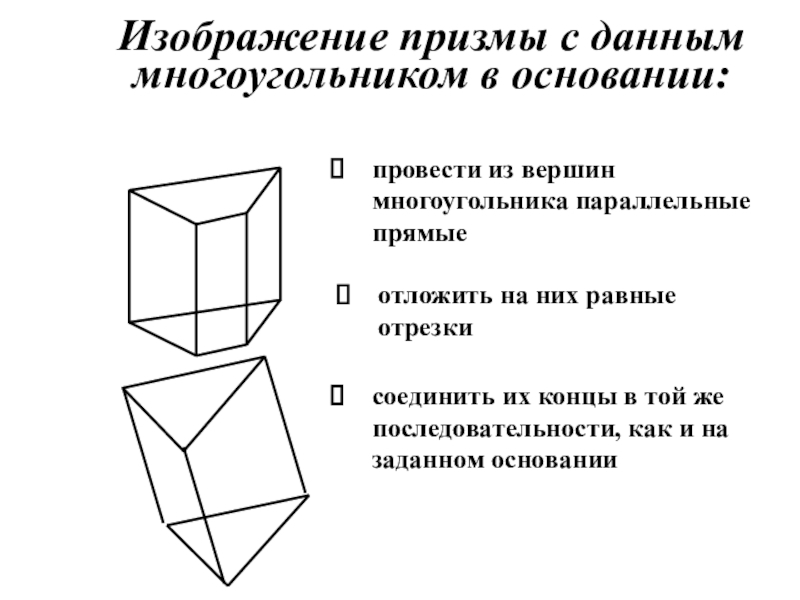
- 21. Изображение призмы с данным многоугольником в основании:
- 22. Площадь поверхности призмыПлощадью полной поверхности призмы называется
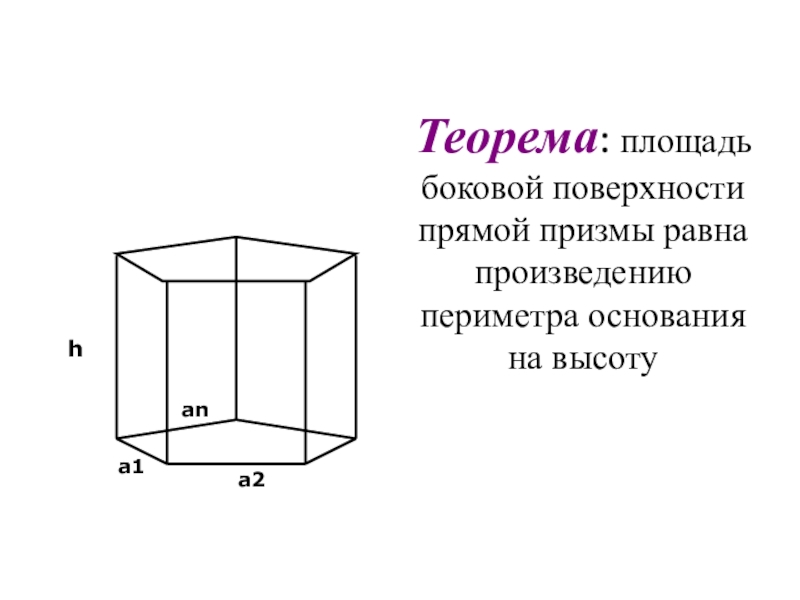
- 23. Теорема: площадь боковой поверхности прямой призмы равна произведению периметра основания на высотуhа1а2аn
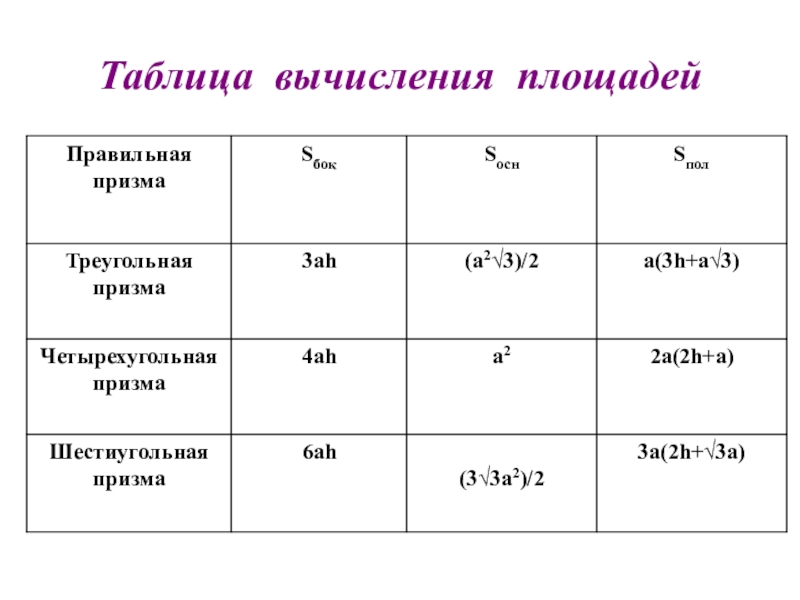
- 24. Таблица вычисления площадей
- 25. Призма в нашей жизни
- 26. Призма в нашей жизни
- 27. «Знания по геометрии и умение пользоваться формулами необходимы почти каждому мастеру или рабочему». Л. Н. Колмогоров
Слайд 2 Многоугольником называется плоская фигура, ограниченная отрезками прямых,
многогранник можно
Слайд 4 Правильные многогранники
Тетраэдр
Гексаэдр
Икосаэдр
Октаэдр
Додекаэдр
Правильными многогранниками называют выпуклые многогранники, все грани
Слайд 5Архимедовыми телами называют выпуклые многогранники, все многогранные углы которых равны, а
Архимедовы тела
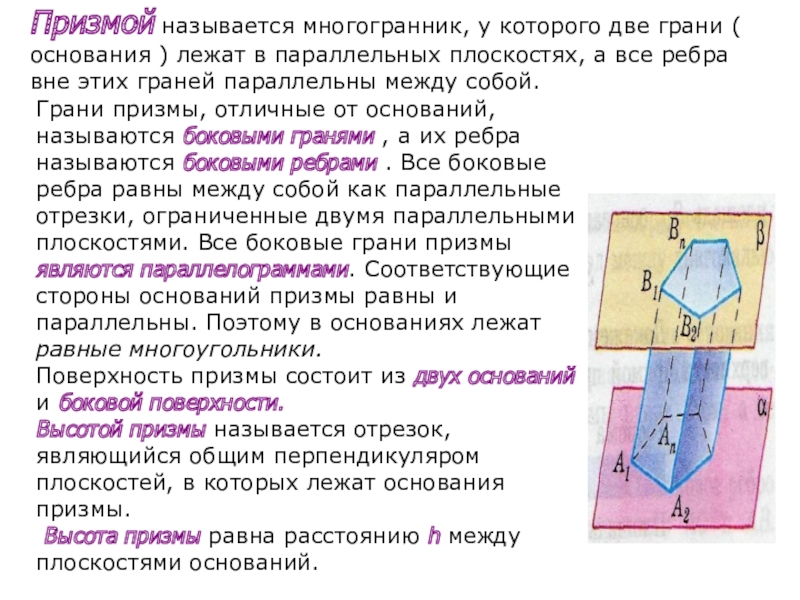
Слайд 12Призмой называется многогранник, у которого две грани ( основания ) лежат
Грани призмы, отличные от оснований, называются боковыми гранями , а их ребра называются боковыми ребрами . Все боковые ребра равны между собой как параллельные отрезки, ограниченные двумя параллельными плоскостями. Все боковые грани призмы являются параллелограммами. Соответствующие стороны оснований призмы равны и параллельны. Поэтому в основаниях лежат равные многоугольники.
Поверхность призмы состоит из двух оснований и боковой поверхности.
Высотой призмы называется отрезок, являющийся общим перпендикуляром плоскостей, в которых лежат основания призмы.
Высота призмы равна расстоянию h между плоскостями оснований.
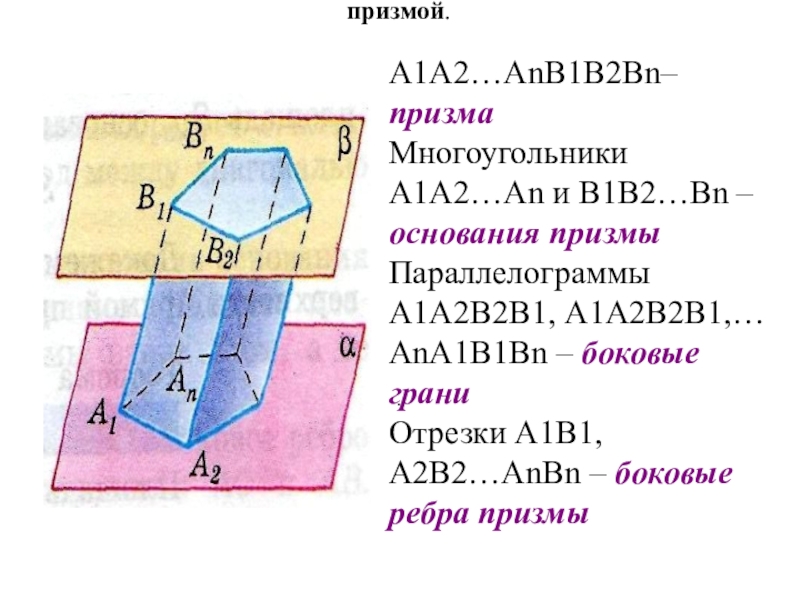
Слайд 13МногогранникМногогранник, поверхность которого состоит из двух равных многоугольниковМногогранник, поверхность которого состоит
А1А2…АnВ1В2Вn– призма
Многоугольники А1А2…Аn и В1В2…Вn – основания призмы
Параллелограммы А1А2В2В1, А1А2В2В1,… АnА1В1Вn – боковые грани
Отрезки А1В1, А2В2…АnBn – боковые ребра призмы
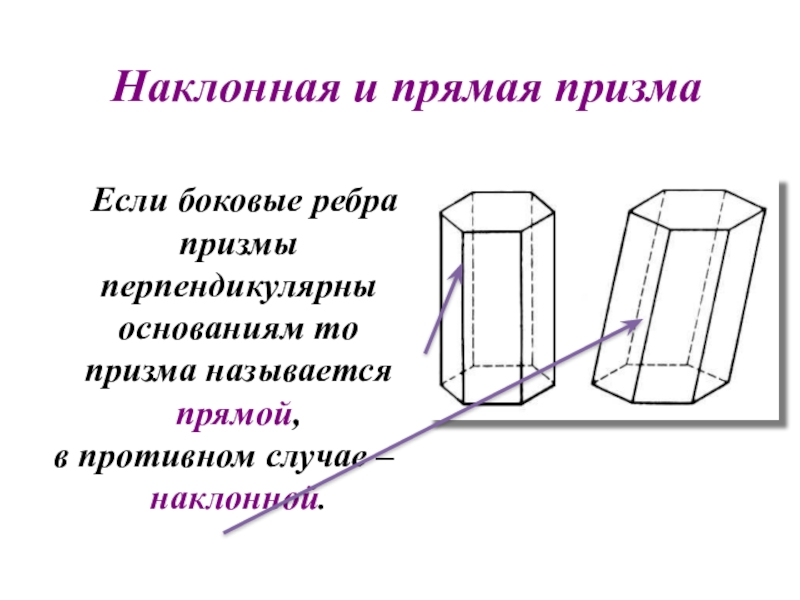
Слайд 15Наклонная и прямая призма
Если боковые ребра призмы перпендикулярны
в противном случае – наклонной.
Слайд 16Правильная призма
Призма называется правильной,
если она прямая
и ее основания -
Слайд 17призма
основания
боковая грань
высота
боковое ребро
A1
An
A2
В1
Вn
В2
A1 A2…. An В1 В2….. Вn – n-угольная призма
Слайд 18Свойства призмы.
1. Основания призмы являются равными многоугольниками.
2. Боковые грани призмы являются параллелограммами.
4.
5. Все боковые ребра равны и параллельны.
6. Противоположные боковые грани равны и параллельны.
Слайд 21Изображение призмы с данным многоугольником в основании:
соединить их концы в
провести из вершин многоугольника параллельные прямые
отложить на них равные отрезки
Слайд 22Площадь поверхности призмы
Площадью полной поверхности призмы называется сумма площадей всех ее
Sполн =Sбок + 2Sосн
Слайд 23Теорема: площадь боковой поверхности прямой призмы равна произведению периметра основания на
h
а1
а2
аn
Слайд 27«Знания по геометрии и умение пользоваться формулами необходимы почти каждому мастеру
Л. Н. Колмогоров