- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по дисциплине ЕН.03 Теория вероятности и математическая статистика на тему Дискретные случайные величины
Содержание
- 1. Презентация по дисциплине ЕН.03 Теория вероятности и математическая статистика на тему Дискретные случайные величины
- 2. Определение случайной величиныСлучайной называют величину, которая в
- 3. Определение непрерывной случайной величиныНепрерывной называют случайную величину,
- 4. Определение функции распределенияФункцией распределения называют функцию F(x),
- 5. Свойства функции распределенияЗначения функции распределения принадлежат отрезку
- 6. Определение дискретной случайной величины (ДСВ)Дискретной (прерывной) называют
- 7. Закон распределения дискретной случайной величиныЗаконом распределения дискретной
- 8. Числовые характеристики случайных величин:математическое ожидание M(X), дисперсия
- 9. Математическое ожиданиеМатематическое ожидание ДСВ M(X) – есть
- 10. Свойства математического ожиданияМатематическое ожидание постоянной величины равно
- 11. Свойства математического ожиданияМатематическое ожидание суммы двух случайных
- 12. Дисперсия ДСВДисперсией (рассеянием) дискретной случайной величины называют
- 13. Свойства дисперсииДисперсия постоянной величины равна 0.Постоянный множитель
- 14. Свойства дисперсииДисперсия разности двух независимых случайных величин
- 15. Среднее квадратическое отклонениеСредним квадратическим отклонением случайной величины X называют квадратный корень из дисперсии:
- 16. Задача 1В результате испытаний 2 приборов (А
- 17. РешениеСредний уровень помех для прибора А: МА(Х)=0·0,7+1·0,2+2·0,06+3·0,04=0,44Для
- 18. Задача 2В денежной лотерее разыгрывается 1 выигрыш
Определение случайной величиныСлучайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Обозначаются случайные величины прописными буквами X, Y,
Слайд 2Определение случайной величины
Случайной называют величину, которая в результате испытания примет одно
и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены.
Обозначаются случайные величины прописными буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами x, y, z.
Обозначаются случайные величины прописными буквами X, Y, Z, а их возможные значения – соответствующими строчными буквами x, y, z.
Слайд 3Определение непрерывной случайной величины
Непрерывной называют случайную величину, которая может принимать все
значения из некоторого конечного или бесконечного промежутка.
Число возможных значений непрерывной случайной величины бесконечно.
Число возможных значений непрерывной случайной величины бесконечно.
Слайд 4Определение функции распределения
Функцией распределения называют функцию F(x), определяющую вероятность того, что
случайная величина X в результате испытаний примет значение, меньшее x, то есть
Слайд 5Свойства функции распределения
Значения функции распределения принадлежат отрезку
, .
F(x) - неубывающая функция.
Вероятность того, что случайная величина примет значение, заключенное в интервале (a;b) равна приращению функции распределения на этом интервале .
Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна 0.
Функция распределения принимает предельные значения и .
F(x) - неубывающая функция.
Вероятность того, что случайная величина примет значение, заключенное в интервале (a;b) равна приращению функции распределения на этом интервале .
Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна 0.
Функция распределения принимает предельные значения и .
,
Слайд 6Определение дискретной случайной величины (ДСВ)
Дискретной (прерывной) называют случайную величину, которая принимает
отдельные, изолированные возможные значения с определенными вероятностями.
Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Пример:
X – количество стульев в аудитории,
Y – уровень помех, который может принимать значения 1, 2, 3.
Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Пример:
X – количество стульев в аудитории,
Y – уровень помех, который может принимать значения 1, 2, 3.
Слайд 7Закон распределения дискретной случайной величины
Законом распределения дискретной случайной величины называют соответствие
между возможными значениями случайной величины и их вероятностями; его можно задать таблично, аналитически (в виде формул) и графически (полигоном или многоугольником распределения).
Сумма вероятностей, с которыми дискретная случайная величина принимает все свои значения, равна единице, т.е. .
Сумма вероятностей, с которыми дискретная случайная величина принимает все свои значения, равна единице, т.е. .
Слайд 8Числовые характеристики случайных величин:
математическое ожидание M(X),
дисперсия D(X),
среднее квадратическое (квадратичное)
отклонение .
Слайд 9Математическое ожидание
Математическое ожидание ДСВ M(X) – есть сумма произведений всех возможных
значений случайной величины на соответствующие им вероятности :
Смысл математического ожидания – среднее значение случайной величины.
Смысл математического ожидания – среднее значение случайной величины.
Слайд 10Свойства математического ожидания
Математическое ожидание постоянной величины равно этой постоянной
Постоянный множитель можно
выносить за символ математического ожидания
Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий
Математическое ожидание произведения нескольких независимых случайных величин равно произведению их математических ожиданий
Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий
Математическое ожидание произведения нескольких независимых случайных величин равно произведению их математических ожиданий
Слайд 11Свойства математического ожидания
Математическое ожидание суммы двух случайных величин равно сумме математических
ожиданий слагаемых
Математическое ожидание суммы нескольких независимых случайных величин равно сумме их математических ожиданий
Математическое ожидание отклонений случайной величины от своего математического ожидания равно нулю
Математическое ожидание числа появления события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании
Математическое ожидание суммы нескольких независимых случайных величин равно сумме их математических ожиданий
Математическое ожидание отклонений случайной величины от своего математического ожидания равно нулю
Математическое ожидание числа появления события А в n независимых испытаниях равно произведению числа испытаний на вероятность появления события в каждом испытании
Слайд 12Дисперсия ДСВ
Дисперсией (рассеянием) дискретной случайной величины называют математическое ожидание квадрата отклонений
случайной величины от ее математического ожидания (не может быть отрицательной).
Для практических расчетов пользуются формулой
где
Для практических расчетов пользуются формулой
где
Слайд 13Свойства дисперсии
Дисперсия постоянной величины равна 0.
Постоянный множитель можно выносить за знак
дисперсии, возводя его в квадрат
Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин
Дисперсия суммы постоянной величины и случайной величины равна дисперсии случайной величины
Дисперсия суммы двух независимых случайных величин равна сумме дисперсий этих величин
Дисперсия суммы постоянной величины и случайной величины равна дисперсии случайной величины
Слайд 14Свойства дисперсии
Дисперсия разности двух независимых случайных величин равна сумме их дисперсий
Дисперсия
числа появлений события A в n независимых испытаниях, в каждом из которых вероятность p появления события постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании
Слайд 15Среднее квадратическое отклонение
Средним квадратическим отклонением случайной величины X называют квадратный корень
из дисперсии:
Слайд 16Задача 1
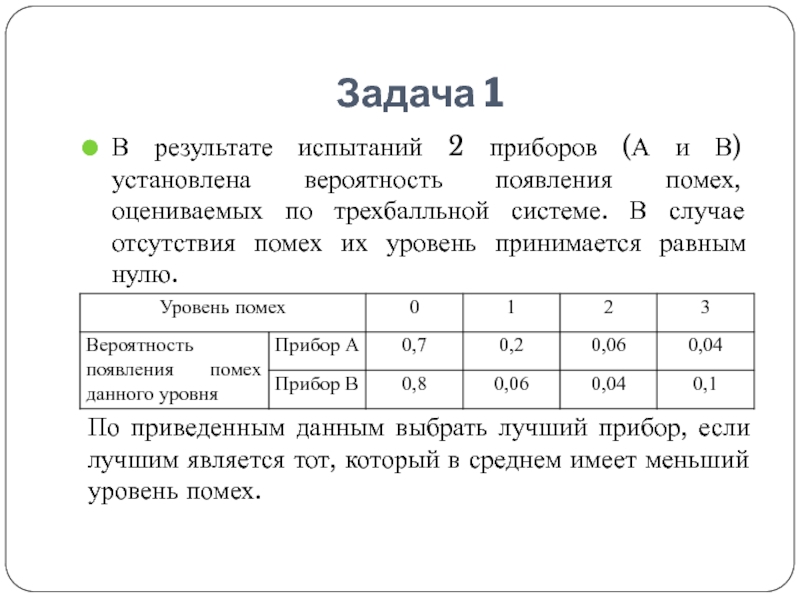
В результате испытаний 2 приборов (А и В) установлена вероятность
появления помех, оцениваемых по трехбалльной системе. В случае отсутствия помех их уровень принимается равным нулю.
По приведенным данным выбрать лучший прибор, если лучшим является тот, который в среднем имеет меньший уровень помех.
По приведенным данным выбрать лучший прибор, если лучшим является тот, который в среднем имеет меньший уровень помех.
Слайд 17Решение
Средний уровень помех для прибора А: МА(Х)=0·0,7+1·0,2+2·0,06+3·0,04=0,44
Для прибора В: МВ(Х)=0·0,8+1·0,06+2·0,04+3·0,1=0,44.
Итак, по
среднему баллу оба прибора равноценны. В качестве дополнительного критерия сравнения используем среднее квадратическое отклонение уровня помех:
Прибор А дает более устойчивые показания относительно средних и, следовательно, он лучше прибора В.
Прибор А дает более устойчивые показания относительно средних и, следовательно, он лучше прибора В.
Слайд 18Задача 2
В денежной лотерее разыгрывается 1 выигрыш в 1000 рублей, 10
выигрышей по 100 рублей, 100 выигрышей по 1 рублю при общем числе билетов 10000. Найти закон распределения случайного выигрыша Х для владельца 1 билета.
Ответ:
Ответ: