- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку по геометрии на тему
Содержание
- 1. Презентация к уроку по геометрии на тему
- 2. Катет Гипотенуза Прямоугольный треугольник –
- 3. Слайд 3
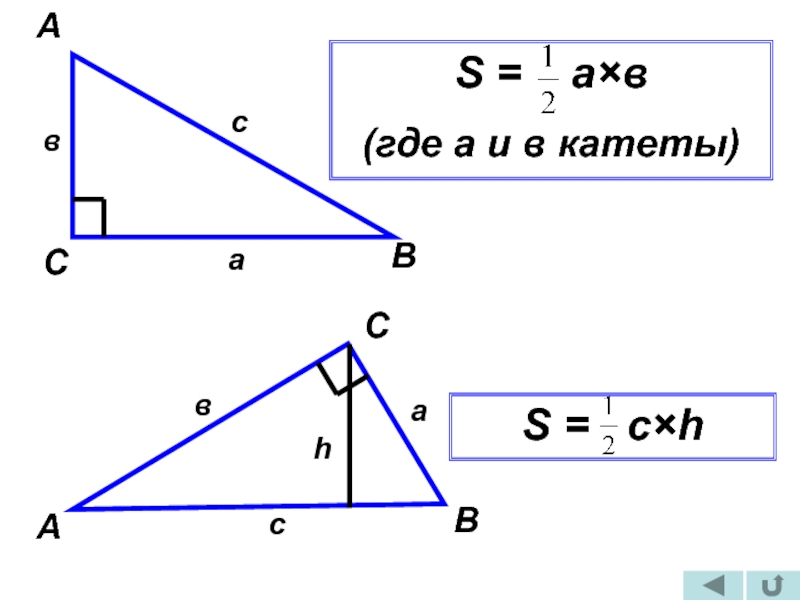
- 4. АВСвасS = а×в(где а и в катеты)АСВасвhS = c×h
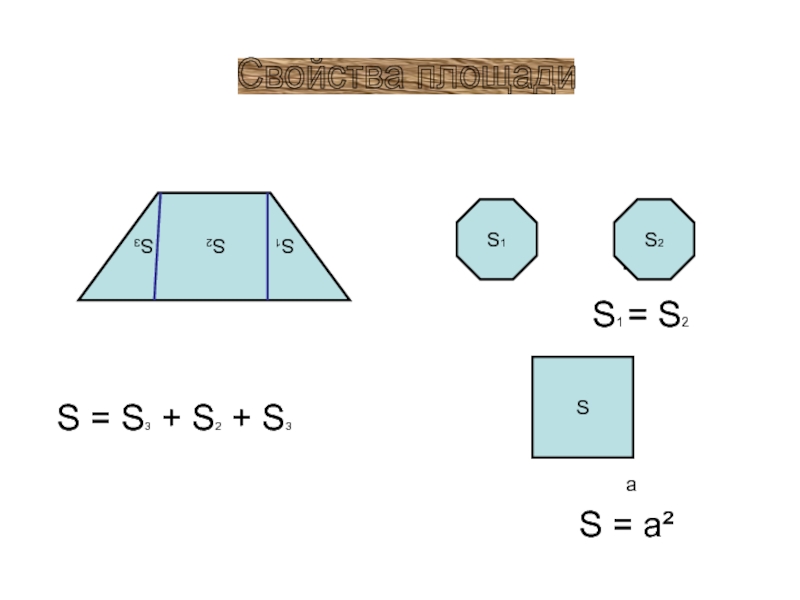
- 5. S = S3 +
- 6. Пифагор Самосский – философ,
- 7. В Южной Италии-
- 8. В научных достижениях Пифагор
- 9. Смерть Пифагора тоже окутана
- 10. Есть и еще одна
- 11. Интересна история теоремы Пифагора. Хотя эта теорема
- 12. Сохранилось древнее предание, что в честь своего
- 13. Раньше знаменитая теорема Пифагора звучала так: площадь
- 14. Теореме Пифагора можно дать
- 15. Тогда площадь квадрата, построенного
- 16. В прямоугольном треугольнике квадрат гипотенузы равен сумме
- 17. А
- 18. DB = 5см, DC =
- 19. A
- 20. Землемеры Древнего Египта для
- 21. Пифагоровы треугольники – это прямоугольные треугольники, у
- 22. Задача № 489 Докажите, что площадь равностороннего
- 23. Доказательство:1) Проведём высоту ВВ , тогда
- 24. Задача № 487 Боковая сторона равнобедренного треугольника
- 25. Решение:1) Известно, что высота, проведённая к основанию
- 26. Если квадрат одной стороны треугольника равен сумме
- 27. Вывод:Доказано утверждение, обратное теореме Пифагора - если
- 28. 1. п.п.54, 55 Доказательство теоремы Пифагора и ей обратной.№493. Найти и разобрать другие доказательства теоремы Пифагора.Домашнее задание
- 29. «Не гоняйся за
Слайд 2
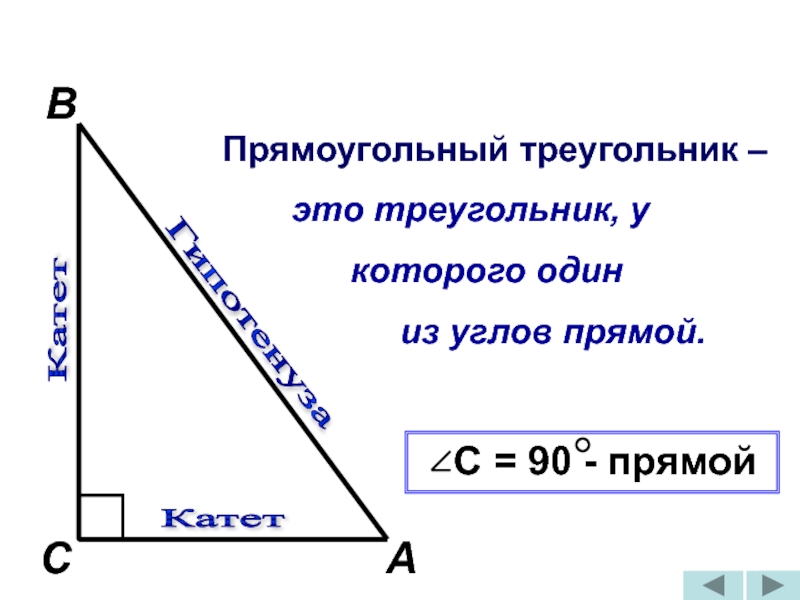
Катет
Гипотенуза
Прямоугольный треугольник –
это треугольник,
которого один
из углов прямой.
С = 90 - прямой
Катет
А
В
С
Слайд 3
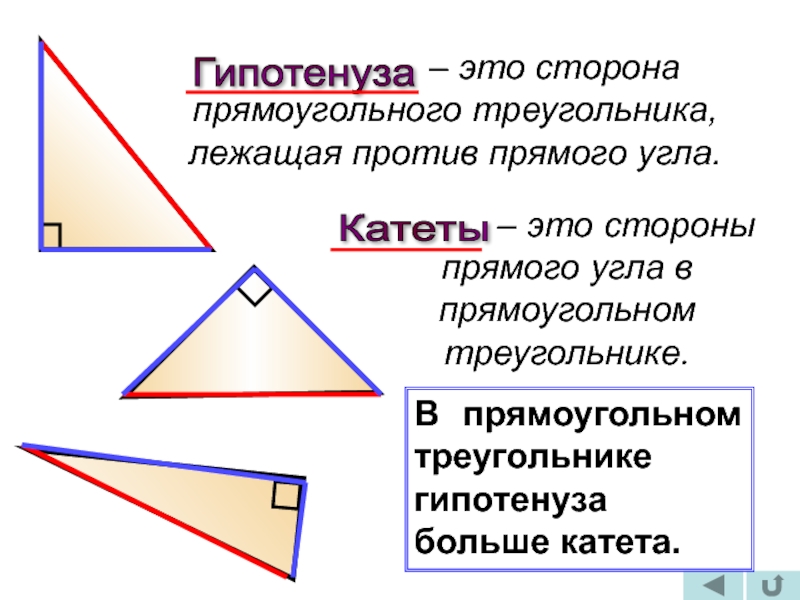
Гипотенуза
– это стороны прямого угла в прямоугольном треугольнике.
Катеты
В прямоугольном треугольнике гипотенуза больше катета.
Слайд 6 Пифагор Самосский – философ, математик, религиозный и политический
Слайд 7 В Южной Италии- г.Кротоне, Пифагор стал
В 18 лет он покинул родной остров и отправился в чужие края. Он побывал на Востоке в Египте, Вавилоне и Финикии.
Слайд 8 В научных достижениях Пифагор прославился своей теоремой «в
Слайд 9 Смерть Пифагора тоже окутана тайной, потому что достоверно
Слайд 10 Есть и еще одна версия, в которой говорится
«Не гоняйся за счастьем: оно всегда находится в тебе самом».
Пифагор.
Слайд 11
Интересна история теоремы Пифагора. Хотя эта теорема и связывается с именем
Слайд 12Сохранилось древнее предание, что в честь своего открытия Пифагор принёс в
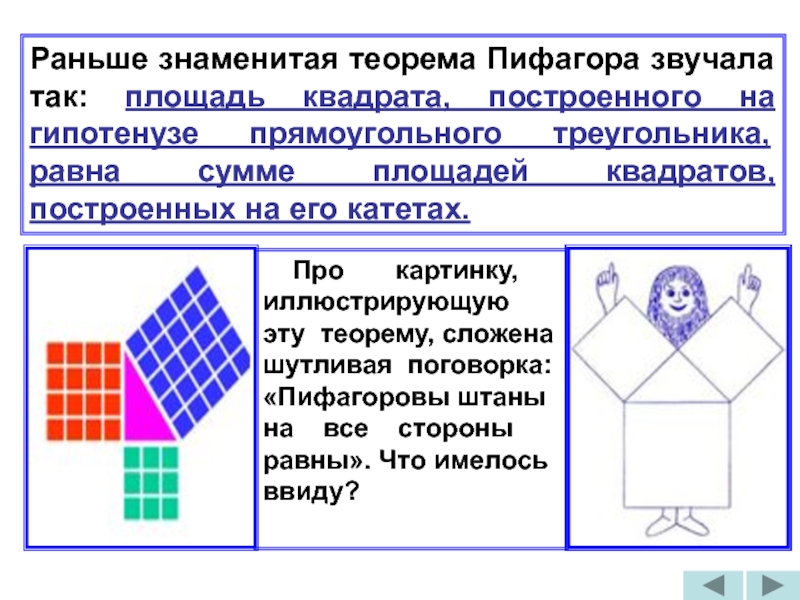
Слайд 13Раньше знаменитая теорема Пифагора звучала так: площадь квадрата, построенного на гипотенузе
Про картинку, иллюстрирующую эту теорему, сложена шутливая поговорка: «Пифагоровы штаны на все стороны равны». Что имелось ввиду?
Слайд 14 Теореме Пифагора можно дать эквивалентную формулировку, применив понятие
Попробуем сформулировать теорему Пифагора по другому:
- Квадрат, построенный на гипотенузе прямоугольного треугольника, равносоставлен с квадратами, построенными на катетах.
Чтобы сформулировать теорему Пифагора в современном изложении, нам необходимо вспомнить, как находится площадь квадрата (нужно сторону квадрата возвести в квадрат).
Слайд 15 Тогда площадь квадрата, построенного на гипотенузе – это
Теперь мы сможем сами дать ещё одну, современную формулировку теоремы Пифагора:
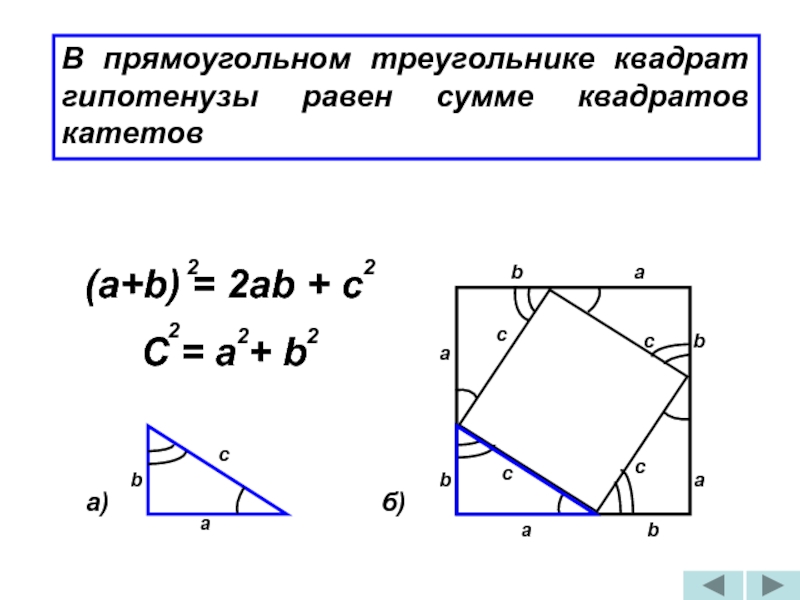
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Слайд 16
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
c
b
a
a
c
b
a
c
b
a
c
b
c
a
b
a)
б)
(a+b) = 2ab
C = a + b
2
2
2
2
2
Слайд 20 Землемеры Древнего Египта для построения прямого угла пользовались
А
В
С
5
4
3
Слайд 21
Пифагоровы треугольники – это прямоугольные треугольники, у которых длины сторон выражаются
Катеты а, b и гипотенуза с таких треугольников выражаются формулами :
a = 2k * m * n ,
b = k ( m - n ) ,
c = k ( m + n ) , где k, m u n – любые натуральные числа, такие, что m > n.
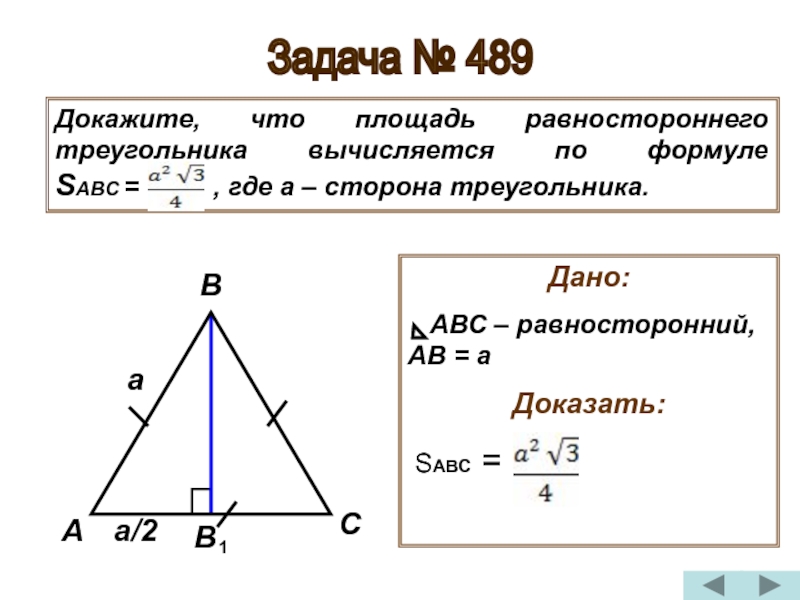
Слайд 22Задача № 489
Докажите, что площадь равностороннего треугольника вычисляется по формуле
Дано:
АВС – равносторонний, АВ = а
Доказать:
SABC =
А
В
В
С
1
а
а/2
Слайд 23
Доказательство:
1) Проведём высоту ВВ , тогда АВВ и
2) Т.к. АВВ - прямоугольный, то АВ = АВ + ВВ
(По теореме Пифагора), отсюда ВВ = АВ - АВ =
= а - =
ВВ = =
3) SABC = 1/2AC * BB = * a * =
Формула выведена, SABC =
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
2
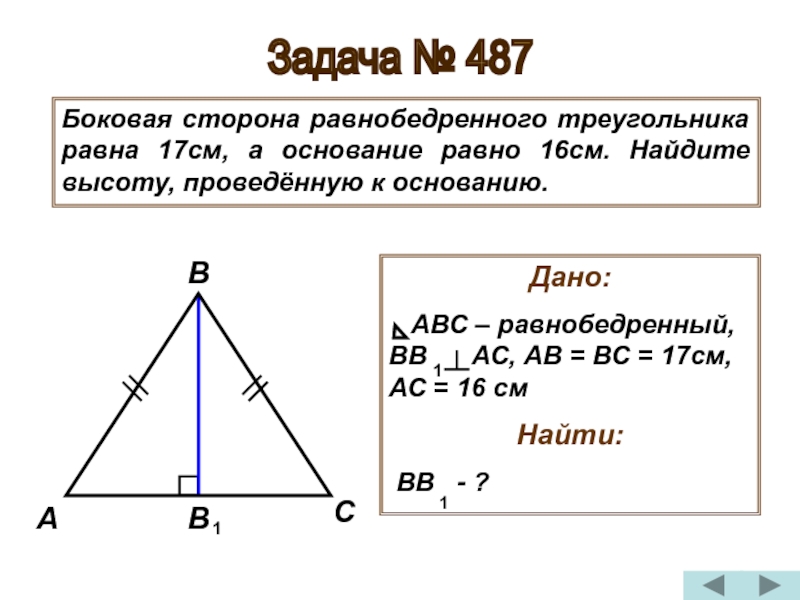
Слайд 24Задача № 487
Боковая сторона равнобедренного треугольника равна 17см, а основание
Дано:
АВС – равнобедренный, ВВ АС, АВ = ВС = 17см, АС = 16 см
Найти:
ВВ - ?
А
С
В
В
1
1
1
Слайд 25Решение:
1) Известно, что высота, проведённая к основанию равнобедренного треугольника, является медианой,
2) Т.к. АВВ - прямоугольный, то АВ = АВ + ВВ
(по теореме Пифагора), отсюда ВВ = АВ - АВ
3) ВВ = 289 – 64 = 225
ВВ = = 15
Ответ: ВВ = 15 см
1
1
1
1
1
1
1
1
1
1
2
2
2
2
2
2
2
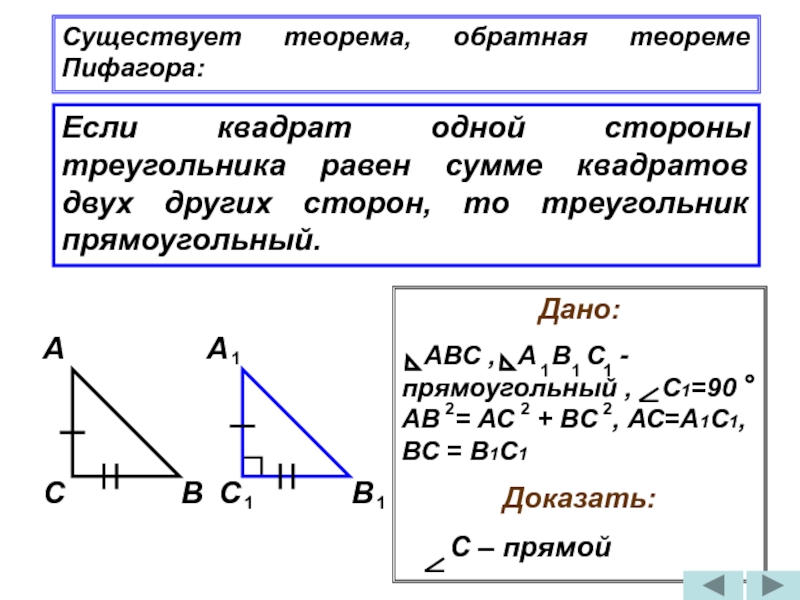
Слайд 26Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон,
Существует теорема, обратная теореме Пифагора:
Дано:
АВС , А В С - прямоугольный , С1=90 АВ = АС + ВС , АС=А1С1, ВС = В1С1
Доказать:
С – прямой
1
1
1
А
А
В
В
С
С
1
1
1
2
2
2
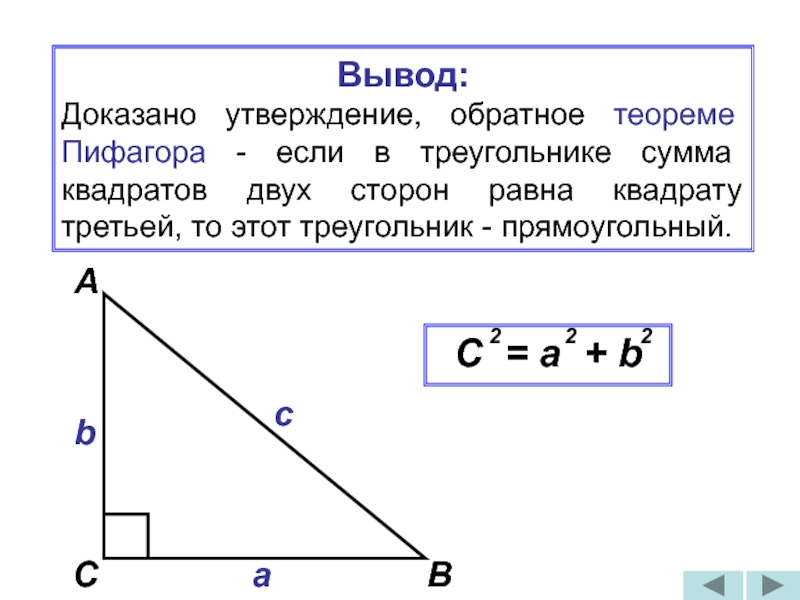
Слайд 27Вывод:
Доказано утверждение, обратное теореме Пифагора - если в треугольнике сумма квадратов
А
В
С
с
а
C = a + b
b
2
2
2
Слайд 281. п.п.54, 55
Доказательство теоремы Пифагора и ей обратной.
№493.
Найти и разобрать другие
Домашнее задание