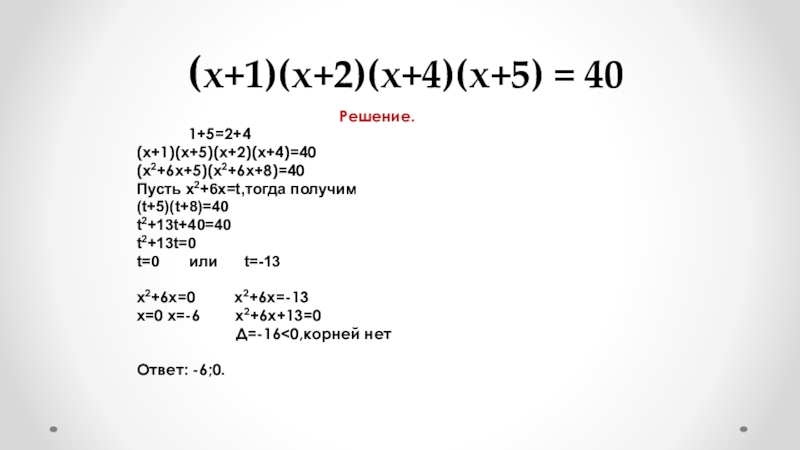- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку на тему Целые уравнения высших степеней и способы их решения
Содержание
- 1. Презентация к уроку на тему Целые уравнения высших степеней и способы их решения
- 2. Девиз урока: «Чем больше я знаю, тем больше умею.»
- 3. ЭпиграфКто ничего не замечает,Тот ничего не изучает.Кто ничего не изучает,Тот вечно хнычет и скучает.(поэт Р.Сеф).
- 4. 2х+5=10х-4
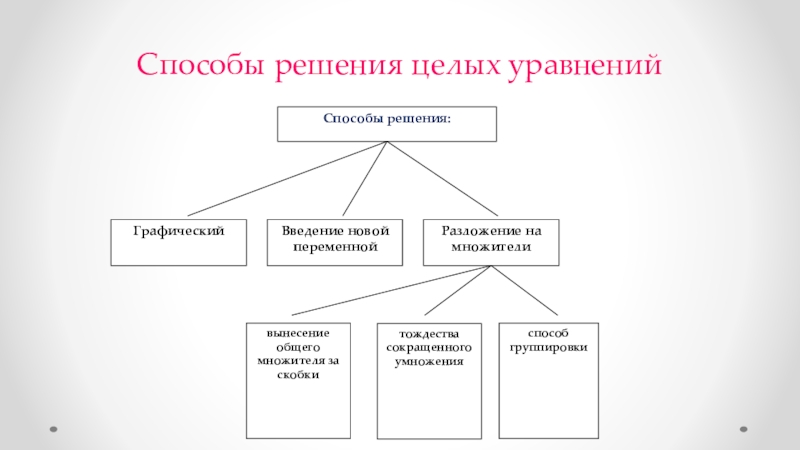
- 5. Способы решения целых уравнений
- 6. Тема урока : Целые уравнения высших степеней и способы их решения.
- 7. Уравнение → способ Биквадратное уравнение.Введение новой переменнойРазложение на множители способом группировкиГрафический способ
- 8. Слайд 8
- 9. Цели урока: узнать новые способы решения целых
- 10. Теорема 1. Если уравнение a0 xn +
- 11. Алгоритм решения целых уравнений
- 12. Физкультминутка
- 13. Посмотри внимательно!
- 14. Алгоритм решения возвратных уравнений
- 15. (х+1)(х+2)(х+4)(х+5) = 40
- 16. (х+1)(х+2)(х+4)(х+5) = 40
- 17. Решить уравнение самостоятельно! (х-1)(х-3)(х+5)(х+7) = 297
- 18. Проверим
- 19. Подведение итогов.Какие цели мы ставили в начале
- 20. « Мне приходиться делить своё время
- 21. Спасибо за урок! До свидания !
Девиз урока: «Чем больше я знаю, тем больше умею.»
Слайд 3Эпиграф
Кто ничего не замечает,
Тот ничего не изучает.
Кто ничего не изучает,
Тот вечно
хнычет и скучает.
(поэт Р.Сеф).
(поэт Р.Сеф).
Слайд 7Уравнение → способ
Биквадратное уравнение.
Введение новой переменной
Разложение на множители способом группировки
Графический
способ
Слайд 9Цели урока:
узнать новые способы решения целых уравнений высших степеней
научиться применять новые способы при решении целых уравнений.
Слайд 10
Теорема 1. Если уравнение a0 xn + a1 xn-1 + …
+an-1 x + an = 0 имеет целые коэффициенты, причём свободный член отличен от нуля, то целыми корнями такого уравнения могут быть только делители свободного члена.
Теорема 2.(теорема Безу). Если число а является корнем многочлена
Р(х)= a0 xn + a1 xn-1 + … +an-1 x + an = 0, то этот многочлен можно без остатка разделить на двучлен (х-а) и представить его в виде произведения (х-а)Р1(х),где Р1(х)-многочлен n-1ой степени.
Теорема 2.(теорема Безу). Если число а является корнем многочлена
Р(х)= a0 xn + a1 xn-1 + … +an-1 x + an = 0, то этот многочлен можно без остатка разделить на двучлен (х-а) и представить его в виде произведения (х-а)Р1(х),где Р1(х)-многочлен n-1ой степени.
Слайд 11Алгоритм решения целых уравнений с помощью теорем:
1. Найти
делители свободного члена.
2.Среди делителей найти корень уравнения путем проверки.
3.Разделить многочлен правой части уравнения на выражение ( х-а), где а – найденный путем подбора корень уравнения.
4.Разложить многочлен на множители.
5. Найти корни уравнения.
6.Записать ответ.
2.Среди делителей найти корень уравнения путем проверки.
3.Разделить многочлен правой части уравнения на выражение ( х-а), где а – найденный путем подбора корень уравнения.
4.Разложить многочлен на множители.
5. Найти корни уравнения.
6.Записать ответ.
Слайд 13Посмотри внимательно!
х4-5х3+6х2-5х+1=0
Определение. Если коэффициенты целого уравнения, равноудалённые от концов , равны, то такое уравнение называется возвратным.
Слайд 15(х+1)(х+2)(х+4)(х+5) = 40
Уравнения вида
(х +
а)(х + b)(x + c)(x + d) = А, где а + d = c + b называются симметрическими.
1+5=2+4
1+5=2+4
Слайд 16 (х+1)(х+2)(х+4)(х+5) = 40
Решение.
1+5=2+4
(х+1)(х+5)(х+2)(х+4)=40
(х2+6х+5)(х2+6х+8)=40
Пусть х2+6х=t,тогда получим
(t+5)(t+8)=40
t2+13t+40=40
t2+13t=0
t=0 или t=-13
х2+6х=0 х2+6х=-13
х=0 х=-6 х2+6х+13=0
Д=-16˂0,корней нет
Ответ: -6;0.
1+5=2+4
(х+1)(х+5)(х+2)(х+4)=40
(х2+6х+5)(х2+6х+8)=40
Пусть х2+6х=t,тогда получим
(t+5)(t+8)=40
t2+13t+40=40
t2+13t=0
t=0 или t=-13
х2+6х=0 х2+6х=-13
х=0 х=-6 х2+6х+13=0
Д=-16˂0,корней нет
Ответ: -6;0.
Слайд 18
Проверим решение!
(х-1)(х-3)(х+5)(х+7) = 297
-1+5=-3+7
(х-1)(х+5)(х-3)(х+7)=297
(х2+4х-5)(х2+4х-21)=297
Пусть t=х2+4х, тогда
(t-5)(t-21)=297
t2-26t -192=0
D=676+768=1444
t1=-6 t2=32
x2+4x=-6 x2+4x=32
x2+4x+6=0 x2+4x-32=0
D=-8˂0 корней нет х=-8 х=4
Ответ: -8; 4.
(х-1)(х+5)(х-3)(х+7)=297
(х2+4х-5)(х2+4х-21)=297
Пусть t=х2+4х, тогда
(t-5)(t-21)=297
t2-26t -192=0
D=676+768=1444
t1=-6 t2=32
x2+4x=-6 x2+4x=32
x2+4x+6=0 x2+4x-32=0
D=-8˂0 корней нет х=-8 х=4
Ответ: -8; 4.
Слайд 19Подведение итогов.
Какие цели мы ставили в начале урока?
Наши цели достигнуты?
Что нового
вы узнали на уроке?
Как вы можете оценить свою работу?
Как вы можете оценить свою работу?
Слайд 20 « Мне приходиться делить своё время между политикой и уравнениями.
Однако уравнение, по – моему, гораздо важнее, потому что политика существует только для данного момента, а уравнение будет существовать вечно».
(Эйнштейн)
(Эйнштейн)