- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Вписанная и описанная окружность в текстах ЕГЭ
Содержание
- 1. Вписанная и описанная окружность в текстах ЕГЭ
- 2. СодержаниеС4 досрочный ЕГЭ апрельС4 Сборник 30 вариантов+800
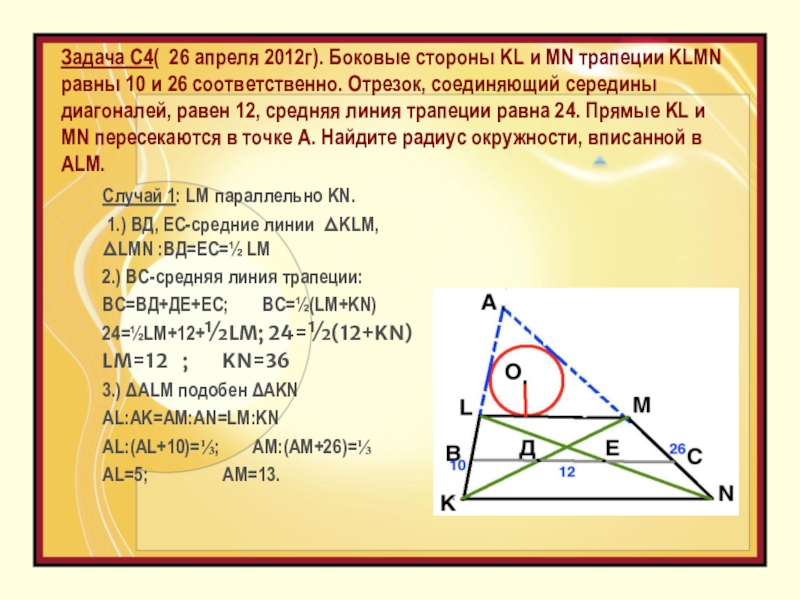
- 3. Задача С4( 26 апреля 2012г). Боковые стороны
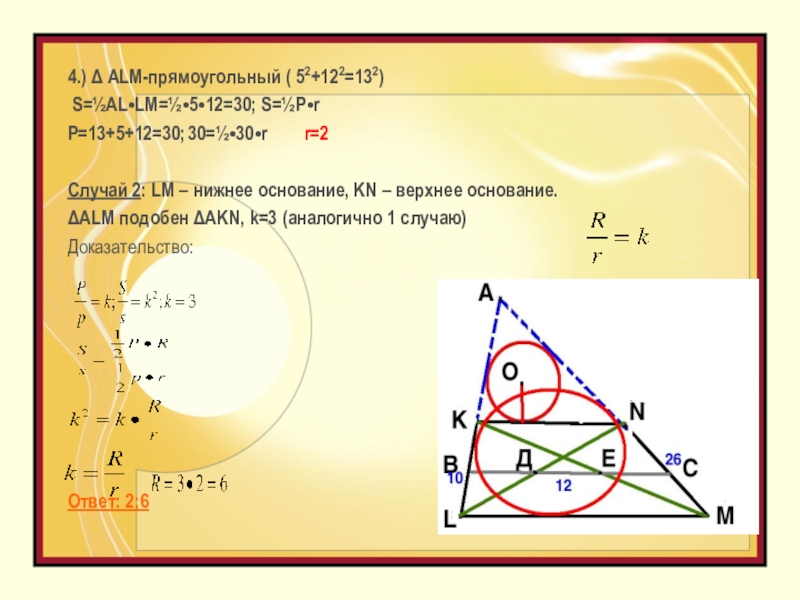
- 4. 4.) Δ ALM-прямоугольный ( 52+122=132) S=½AL•LM=½•5•12=30; S=½P•rP=13+5+12=30; 30=½•30•r
- 5. Задача С4( Сборник 30 вариантов+800 заданий )
- 6. Случай 2: Угол ACB – тупой,
- 7. Решение:Обе точки K и L не могут
- 8. Случай 2: Точка K лежит на продолжении
- 9. Задача С4 (ЕГЭ 2012 восток). Основание равнобедренного
- 10. Случай 2:1.) Из ∆BMP Из ∆AQN Т.к. MNQP-прямоугольник, то QP=MN=2r.2.) AB=AQ+QP+PBОтвет:
- 11. Похожие задачи на ЕГЭ 2012
- 12. Задача С4( Сборник 30 вариантов+800 заданий )В
- 13. Случай 2: ΔАВС-тупоугольный. Тогда ΔAMN подобен
- 14. Литература:МАТЕМАТИКА ЕГЭ 2012 Планиметрические задачи с неоднозначностью
Слайд 1 Вписанная и описанная окружность
в текстах ЕГЭ
Справочное пособие для учащихся
Подготовила: учитель
Слайд 2
Содержание
С4 досрочный ЕГЭ апрель
С4 Сборник 30 вариантов+800 заданий
С4 ЕГЭ
С4 ЕГЭ
С4 Сборник 30 вариантов
+800 заданий
Слайд 3Задача С4( 26 апреля 2012г). Боковые стороны KL и MN трапеции
Случай 1: LM параллельно KN.
1.) ВД, ЕС-средние линии ΔKLM, ΔLMN :ВД=ЕС=½ LM
2.) BC-средняя линия трапеции:
ВС=ВД+ДЕ+ЕС; BC=½(LM+KN)
24=½LM+12+½LM; 24=½(12+KN)
LM=12 ; KN=36
3.) ΔALM подобен ΔAKN
AL:AK=AM:AN=LM:KN
AL:(AL+10)=⅓; AM:(AM+26)=⅓
AL=5; AM=13.
Слайд 44.) Δ ALM-прямоугольный ( 52+122=132)
S=½AL•LM=½•5•12=30; S=½P•r
P=13+5+12=30; 30=½•30•r
Случай 2: LM – нижнее основание, KN – верхнее основание.
ΔALM подобен ΔAKN, k=3 (аналогично 1 случаю)
Доказательство:
Ответ: 2;6
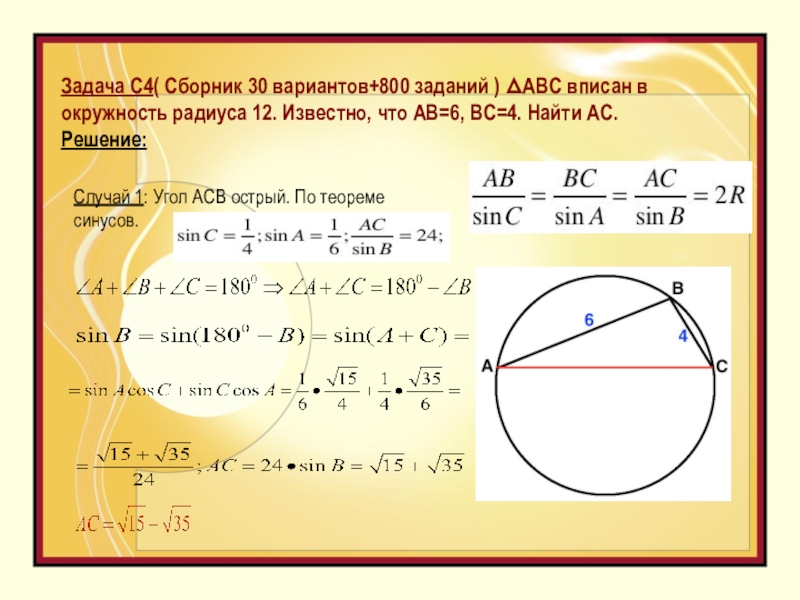
Слайд 5Задача С4( Сборник 30 вариантов+800 заданий ) ΔАВС вписан в окружность
Случай 1: Угол ACB острый. По теореме синусов.
Слайд 6Случай 2: Угол ACB – тупой,
Задача С4 (ЕГЭ 2012 запад). В ∆ABC известны AB=5, BC=6, AC=7. Окружность, проходящая через точки A и C, пересекает прямые BA и BC соответственно в точках K и L, отличных от вершин треугольника. Отрезок KL касается окружности, вписанной в ∆ABC. Найдите длину отрезка KL.
Слайд 7Решение:Обе точки K и L не могут лежать вне ∆АВС, поскольку
Случай 1: Пусть обе точки K и L лежат на сторонах ∆АВС.
1.)AKLC-вписанный 4-хугольник, тогда
подобен ( по двум углам)
с K-коэффициентом подобия.
2.)AKLC-описанный 4-хугольник, тогда
AK+LC=KL+AC, AB(1-k)+CB(1-k)=(1+k)AC,
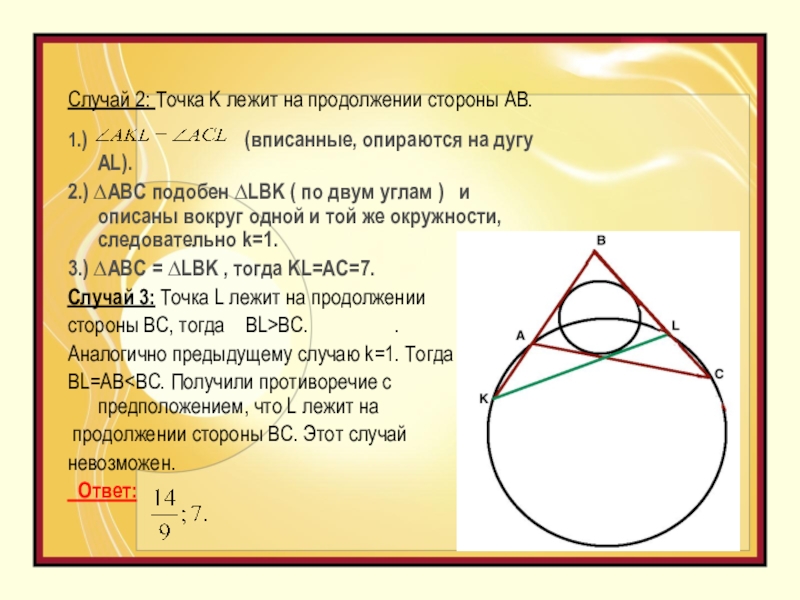
Слайд 8Случай 2: Точка K лежит на продолжении стороны АВ.
1.)
2.) ∆АВС подобен ∆LBK ( по двум углам ) и описаны вокруг одной и той же окружности, следовательно k=1.
3.) ∆АВС = ∆LBK , тогда KL=AC=7.
Случай 3: Точка L лежит на продолжении
стороны ВС, тогда BL>BC. .
Аналогично предыдущему случаю k=1. Тогда
BL=AB
невозможен.
Ответ:
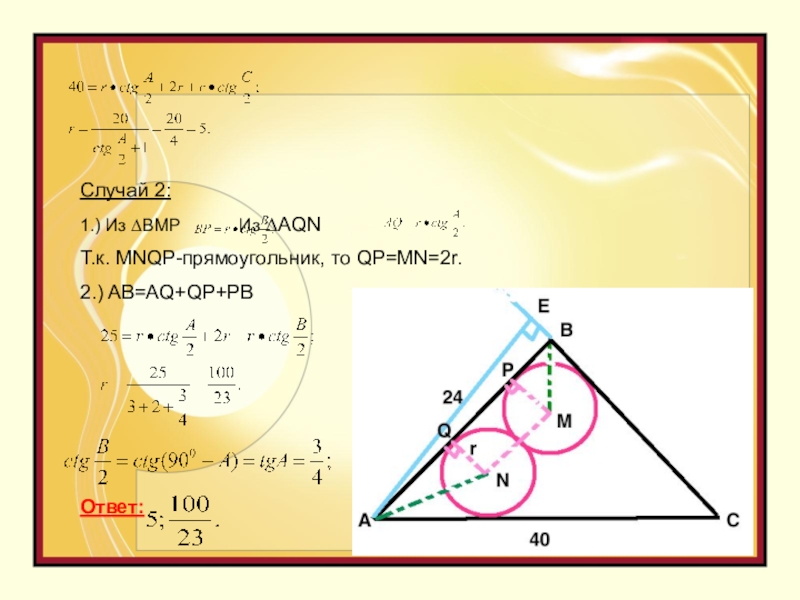
Слайд 9Задача С4 (ЕГЭ 2012 восток). Основание равнобедренного треугольника равно 40, а
Случай 1:∆АВС-равнобедренный,
1.) Из ∆АЕС
2.) Из ∆BHС
3.) Из ∆AMQ
4.) ∆AMQ= ∆PNC ( по катету и
противолежащему углу), тогда AQ=PC;
MNPQ-прямоугольник, QP=2r.
5.) AC=AQ+QP+PC
Слайд 12Задача С4( Сборник 30 вариантов+800 заданий )В ΔАВС проведены высоты BM
Случай 1: ΔАВС-остроугольный.
1.) Т. к. Y-центр описанной окружности, то
2.)По теореме синусов
3.)Т. к. ВМ и CN- высоты ΔАВС, то ΔAMN подобен
ΔАВС
C
4.)
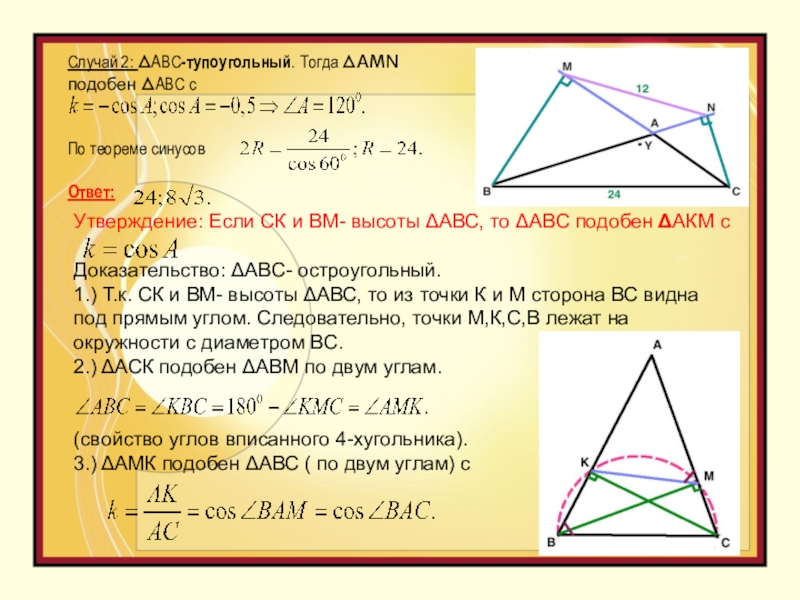
Слайд 13Случай 2: ΔАВС-тупоугольный. Тогда ΔAMN подобен ΔАВС с
Утверждение: Если СК и ВМ- высоты ΔАВС, то ΔАВС подобен ΔАКМ с
Доказательство: ΔАВС- остроугольный.
1.) Т.к. СК и ВМ- высоты ΔАВС, то из точки К и М сторона ВС видна под прямым углом. Следовательно, точки М,К,С,В лежат на окружности с диаметром ВС.
2.) ΔАСК подобен ΔАВМ по двум углам.
(свойство углов вписанного 4-хугольника).
3.) ΔАМК подобен ΔАВС ( по двум углам) с
Слайд 14Литература:
МАТЕМАТИКА ЕГЭ 2012 Планиметрические задачи с неоднозначностью в условии (многовариантные задачи)
Единый государственный экзамен по МАТЕМАТИКЕ 2012 (варианты Восток, Запад.)
Сборник ЕГЭ 2012. Математика. 30 вариантов типовых тестовых заданий и 800 заданий части 2(С)/ И. Р. Высоцкий, П.И.Захаров и др. /Под ред. А. Л. Семёнова, И. В. Ященко.-2012 год.
Подготовка к С4 Вписанные и описанные окружности Материал разработан преподавателем математики подготовительных курсов Учебного центра «Азъ» Трубецким Алексеем Петровичем© Учебный центр «Азъ», 2012
Гордин Р. К. ЕГЭ 2010. Математика. Задача С4/ Под ред. А. Л. Семёнова, И. В. Ященко. Разработано МИОО, 2010 год.