- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Мир правильных многогранников
Содержание
- 1. Мир правильных многогранников
- 2. Что узнаем на уроке?Какие многогранники называются правильными?Сколько
- 3. Правильный многогранник . определениеПравильный многогранник – это…Выпуклый
- 4. Сколько видов правильных многогранников??Пять видов
- 5. Слайд 5
- 6. правильный Тетраэдр
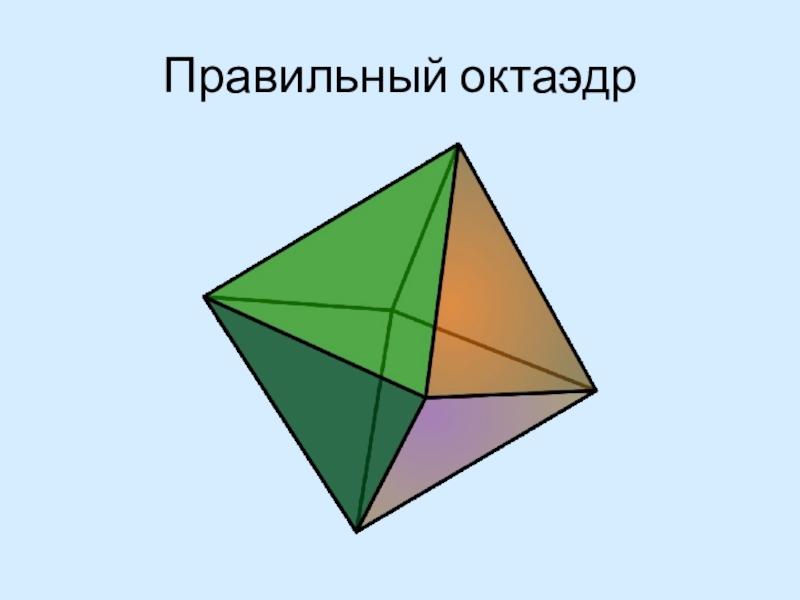
- 7. Правильный октаэдр
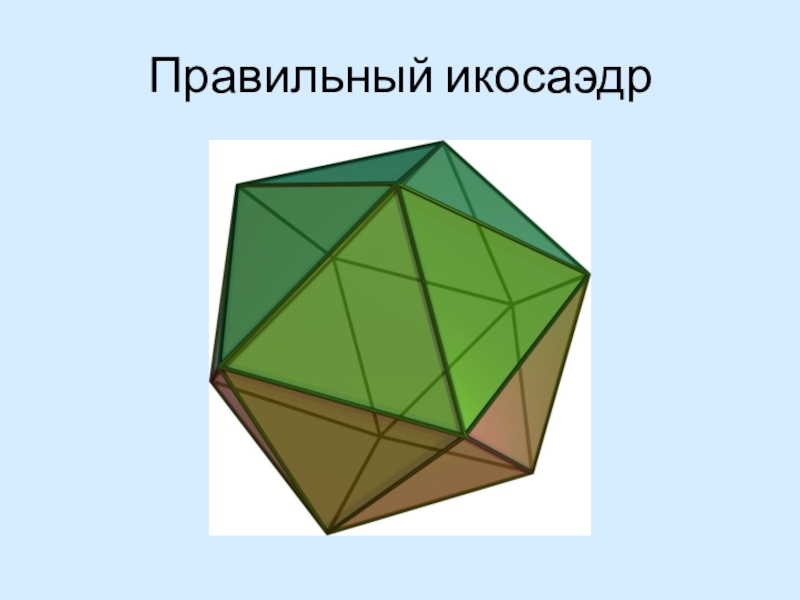
- 8. Правильный икосаэдр
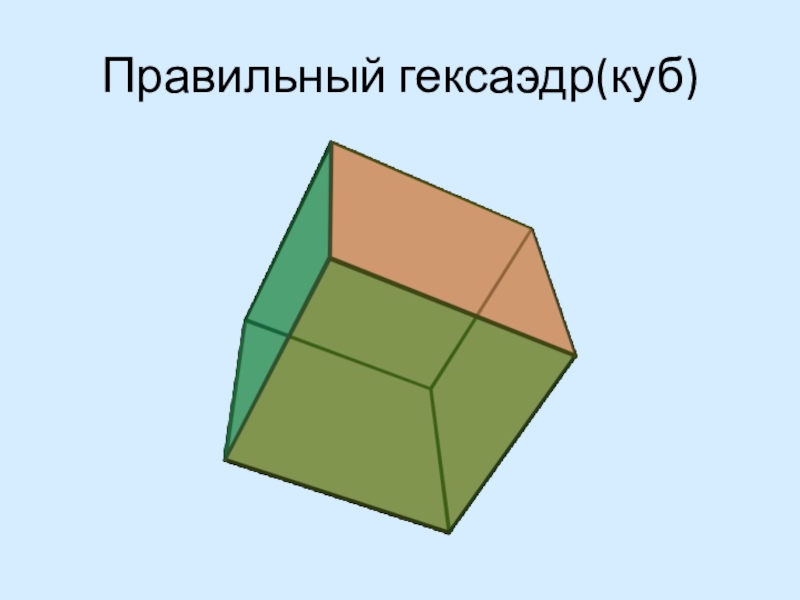
- 9. Правильный гексаэдр(куб)
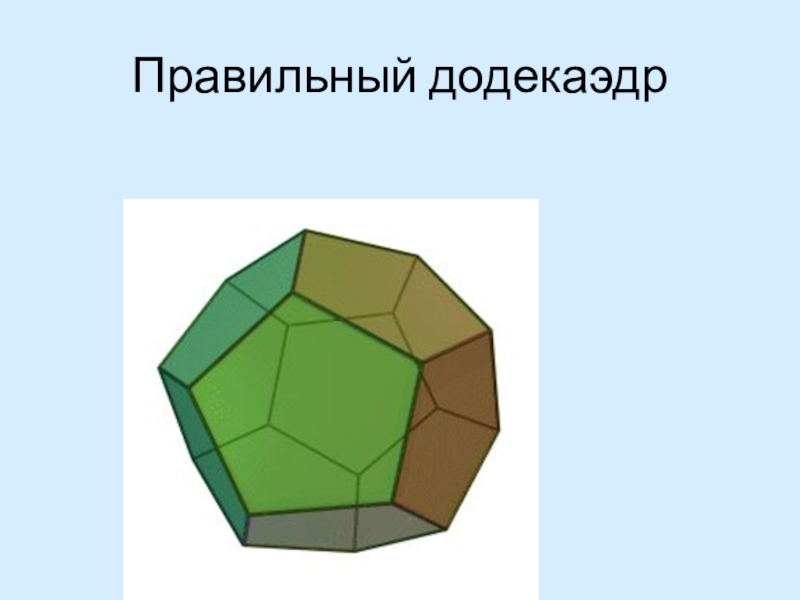
- 10. Правильный додекаэдр
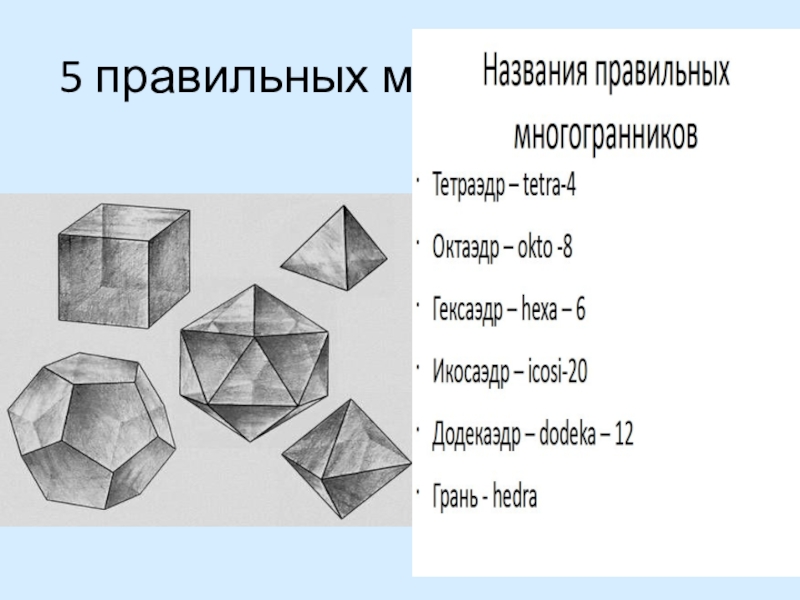
- 11. 5 правильных многогранников
- 12. 4 грани, 4 вершины и 6 ребер.Сумма
- 13. Следствие теоремы ЭйлераN(Г) = 4m:(2m+2n-mn)N(Р) = 2mn:(2m+2n-mn)N(В)
- 14. Правильные многогранники
- 15. Формула Л. Эйлера(18 век) N(в) – N(р) + N(г) = 2
- 16. Слайд 16
- 17. Мир правильных многогранников
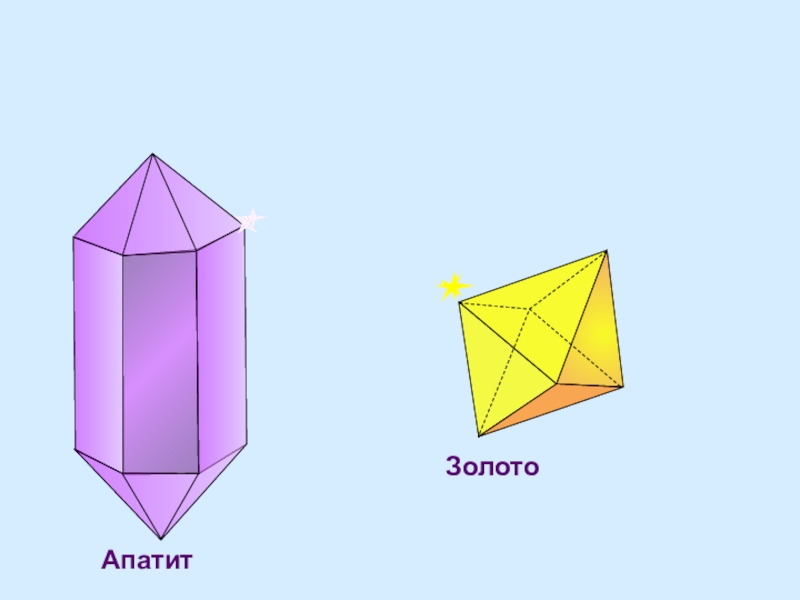
- 18. Золото
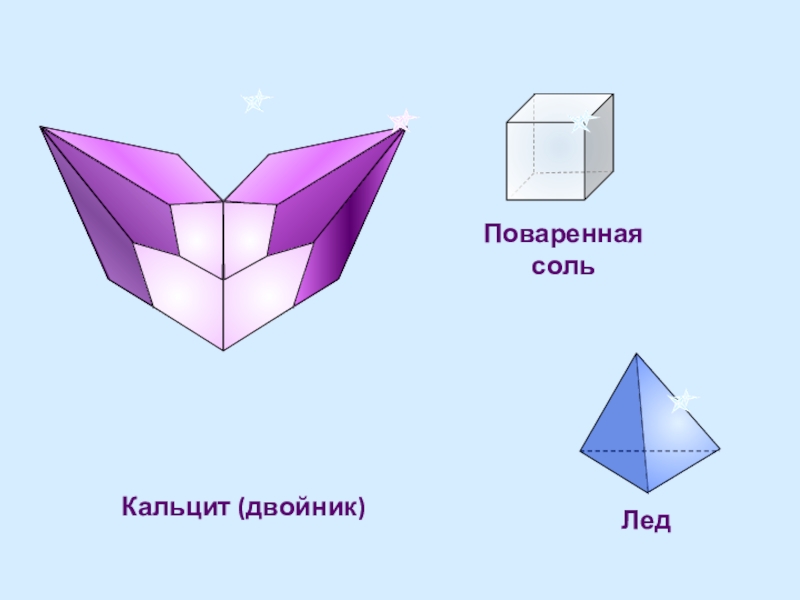
- 19. Кальцит (двойник)
- 20. Форма икосаэдра скелет одноклеточного организма - Феодарии
- 21. Первым свойства правильных многогранников описал древнегреческий ученый
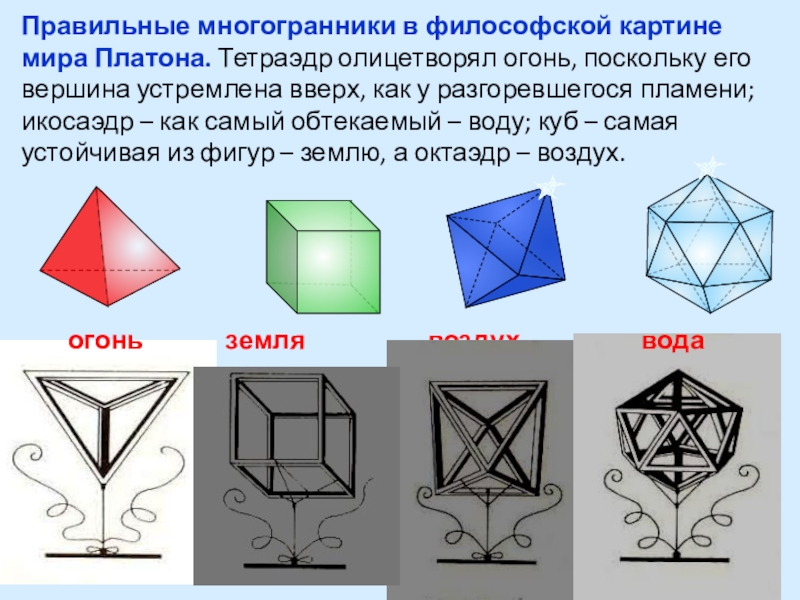
- 22. Правильные многогранники в философской картине мира Платона.
- 23. Пятый многогранник – додекаэдр символизировал весь мир и почитался главнейшим.
- 24. Большой интерес к формам правильных многогранников проявляли
- 25. Архимед287 – 212 гг. до н.э.
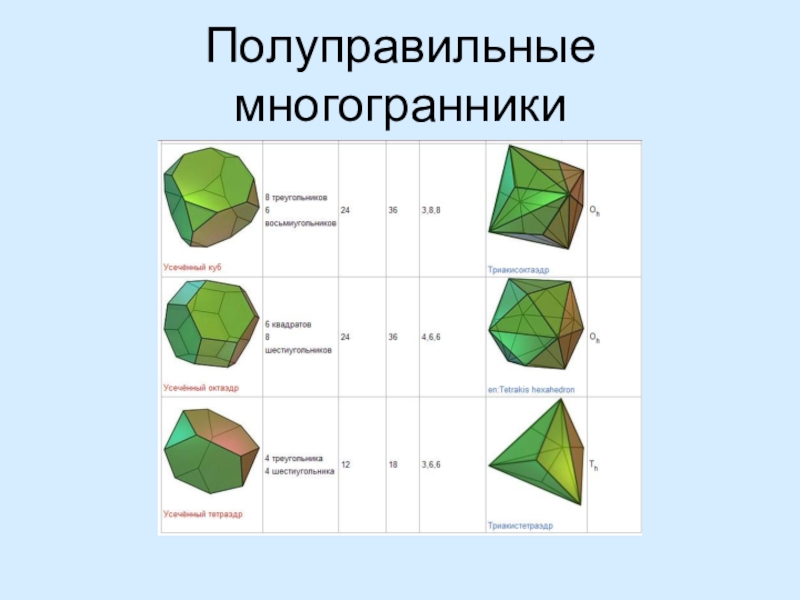
- 26. Полуправильные многогранники
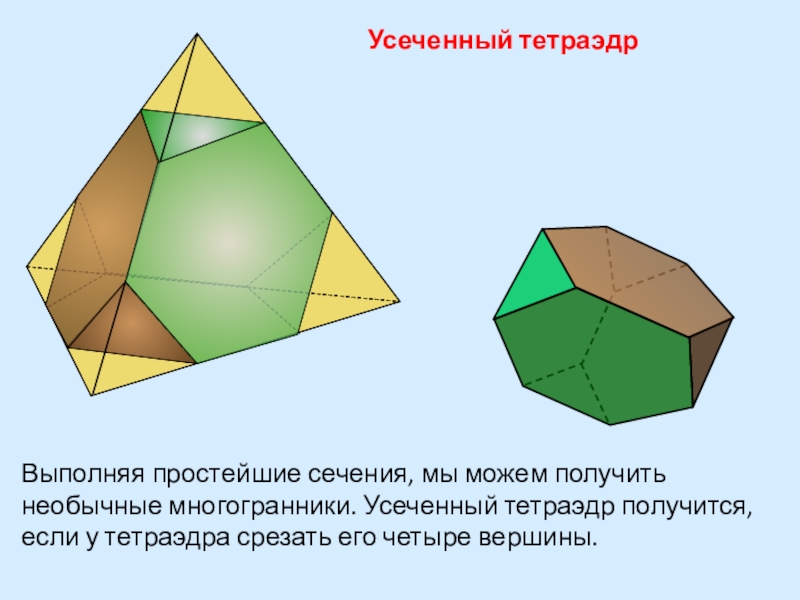
- 27. Усеченный тетраэдрВыполняя простейшие сечения, мы можем получить
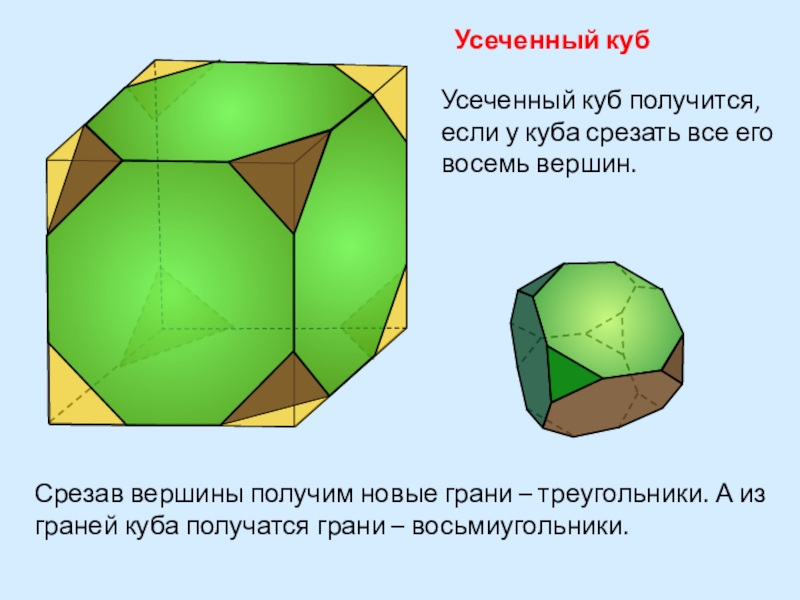
- 28. Усеченный кубСрезав вершины получим новые грани –
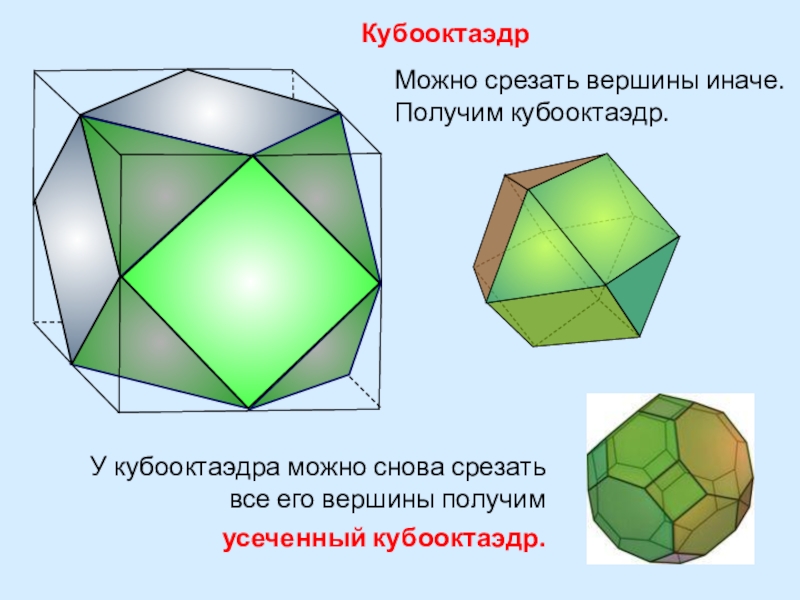
- 29. КубооктаэдрМожно срезать вершины иначе. Получим кубооктаэдр.
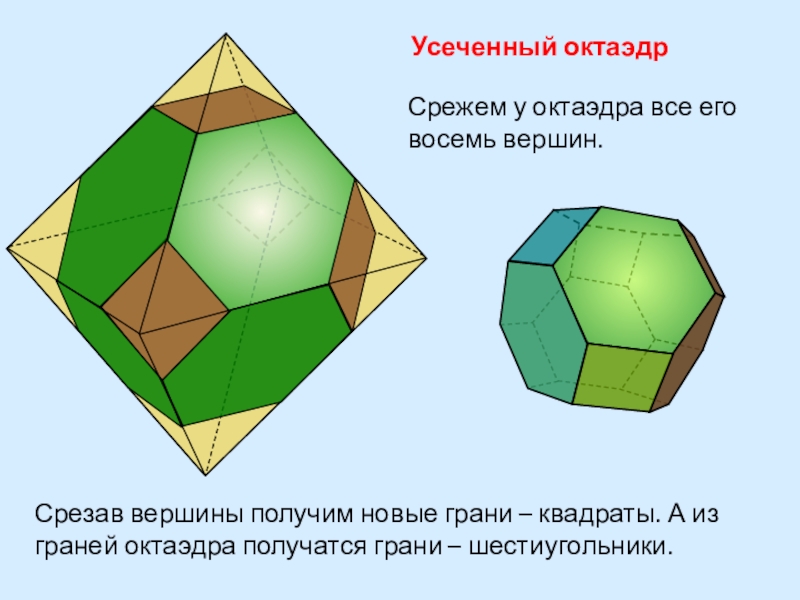
- 30. Усеченный октаэдрСрежем у октаэдра все его восемь
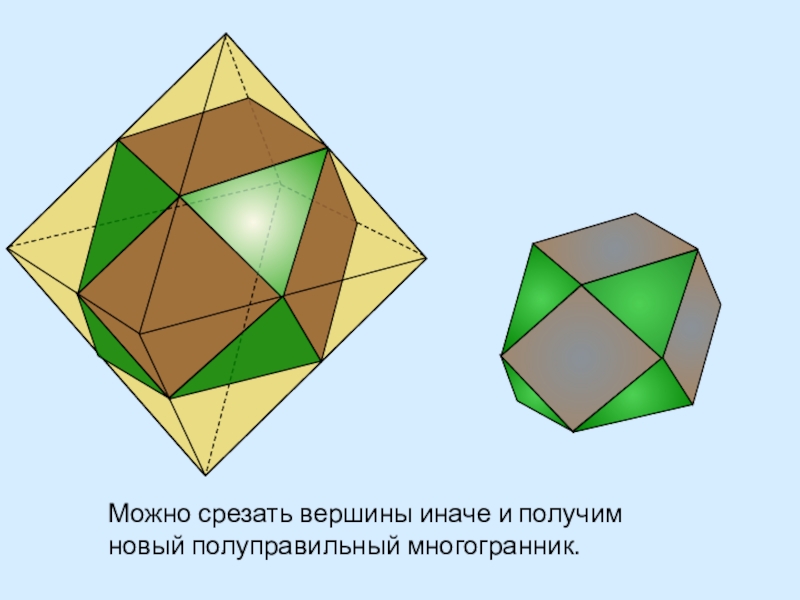
- 31. Можно срезать вершины иначе и получим новый полуправильный многогранник.
- 32. Срезав вершины икосаэдра, получим новые грани пятиугольники,
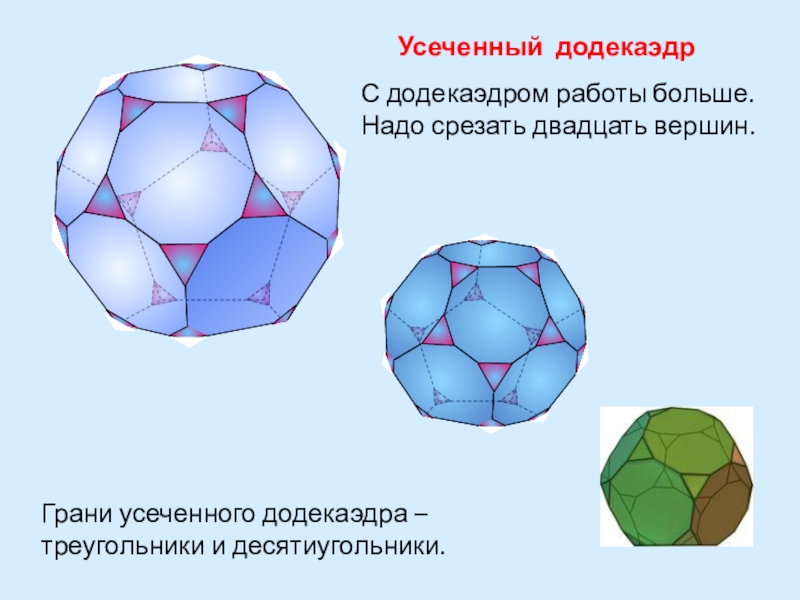
- 33. Усеченный додекаэдрС додекаэдром работы больше. Надо срезать двадцать вершин.Грани усеченного додекаэдра – треугольники и десятиугольники.
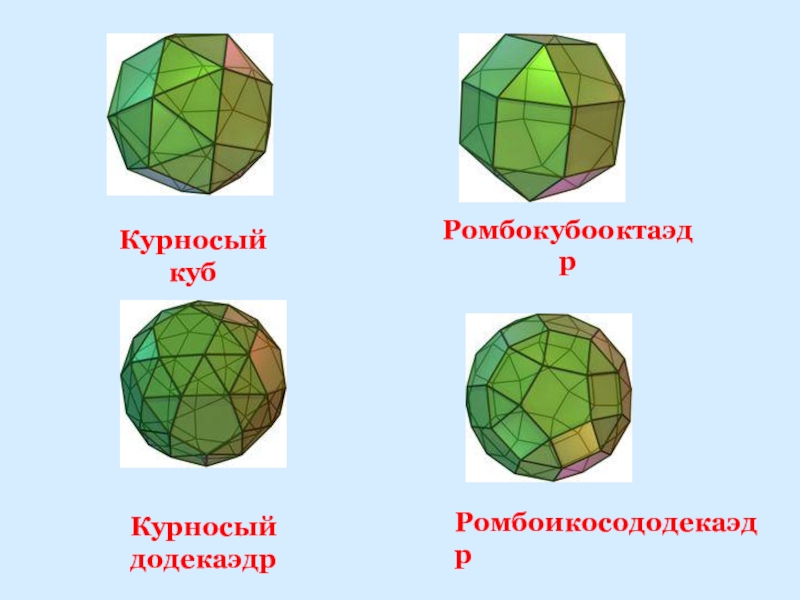
- 34. Курносый кубКурносый додекаэдр
- 35. Многогранники
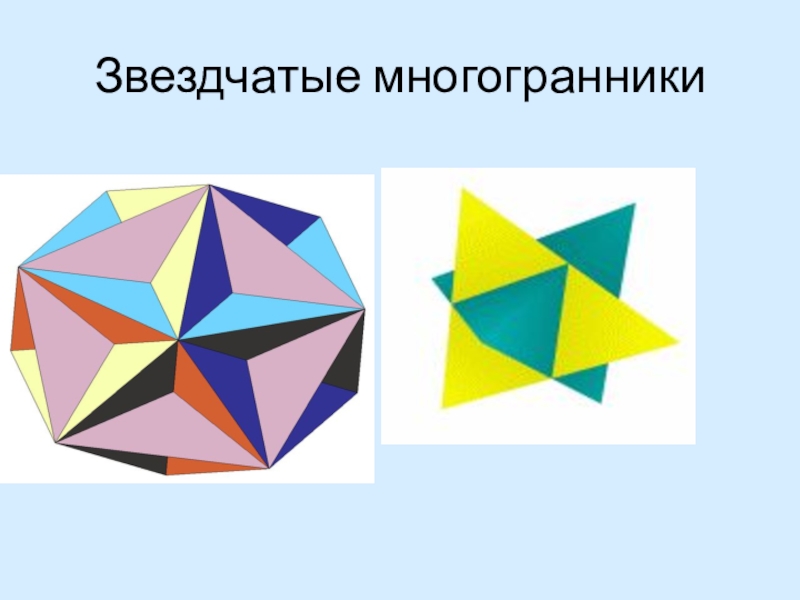
- 36. Звездчатые многогранники
Что узнаем на уроке?Какие многогранники называются правильными?Сколько существует видов правильных многогранников?Существование правильных многогранников в природеДругие красивые виды многогранников
Слайд 2Что узнаем на уроке?
Какие многогранники называются правильными?
Сколько существует видов правильных многогранников?
Существование
правильных многогранников в природе
Другие красивые виды многогранников
Другие красивые виды многогранников
Слайд 3Правильный многогранник . определение
Правильный многогранник – это…
Выпуклый многогранник называется правильным, если
все его грани – равные правильные многоугольники и в каждой его вершине сходится равное число ребер.
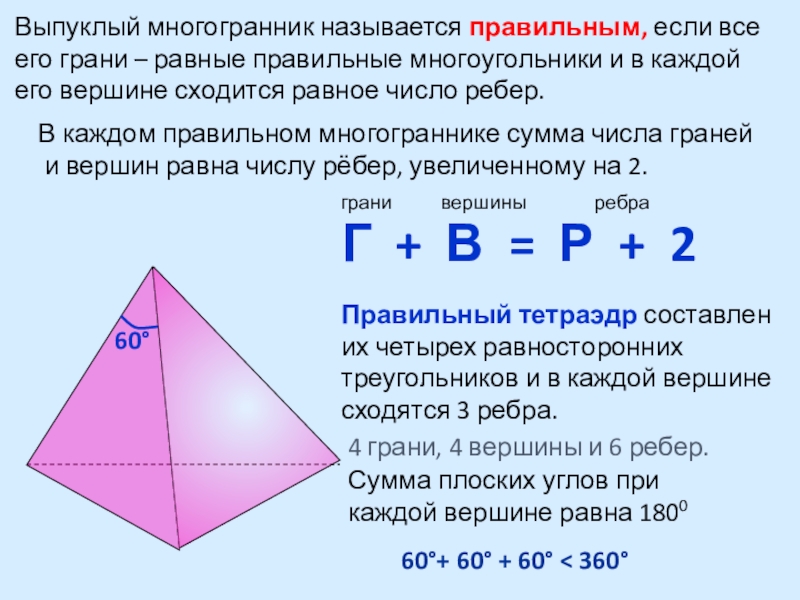
Слайд 124 грани, 4 вершины и 6 ребер.
Сумма плоских углов при каждой
вершине равна 1800
Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и в каждой его вершине сходится равное число ребер.
В каждом правильном многограннике сумма числа граней и вершин равна числу рёбер, увеличенному на 2.
60+ 60 + 60 < 360
Слайд 13Следствие теоремы Эйлера
N(Г) = 4m:(2m+2n-mn)
N(Р) = 2mn:(2m+2n-mn)
N(В) = 4n:(2m+2n-mn)
Где m- ребер
сходящихся к каждой вершине
n- ребер каждой грани
n- ребер каждой грани
Слайд 21Первым свойства правильных многогранников описал древнегреческий ученый Платон. Именно поэтому правильные
многогранники называют также телами Платона.
Платон
428 – 348 г. до н.э.
Платон считал, что мир строится из четырёх «стихий» - огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.
Слайд 22Правильные многогранники в философской картине мира Платона. Тетраэдр олицетворял огонь, поскольку
его вершина устремлена вверх, как у разгоревшегося пламени; икосаэдр – как самый обтекаемый – воду; куб – самая устойчивая из фигур – землю, а октаэдр – воздух.
Слайд 24Большой интерес к формам правильных многогранников проявляли скульпторы, архитекторы, художники. Их
поражало совершенство, гармония многогранников. Леонардо да Винчи (1452 – 1519) увлекался теорией многогранников и часто изображал их на своих полотнах. Сальвадор Дали на картине «Тайная вечеря» изобразил И. Христа со своими учениками на фоне огромного прозрачного додекаэдра.
Слайд 25Архимед
287 – 212 гг. до н.э.
Это многогранники, которые получаются
из платоновых тел в результате их усечения.
усечённый тетраэдр,
усечённый гексаэдр (куб),
усечённый октаэдр,
усечённый додекаэдр,
усечённый икосаэдр.
усечённый тетраэдр,
усечённый гексаэдр (куб),
усечённый октаэдр,
усечённый додекаэдр,
усечённый икосаэдр.
Архимед описал
полуправильные многогранники
Слайд 27Усеченный тетраэдр
Выполняя простейшие сечения, мы можем получить необычные многогранники. Усеченный тетраэдр
получится, если у тетраэдра срезать его четыре вершины.
Слайд 28Усеченный куб
Срезав вершины получим новые грани – треугольники. А из граней
куба получатся грани – восьмиугольники.
Усеченный куб получится, если у куба срезать все его восемь вершин.
Слайд 30Усеченный октаэдр
Срежем у октаэдра все его восемь вершин.
Срезав вершины получим новые
грани – квадраты. А из граней октаэдра получатся грани – шестиугольники.
Слайд 32Срезав вершины икосаэдра, получим новые грани пятиугольники, а грани икосаэдра превратятся
в шестиугольники.
Срезав вершины иначе получим другой многогранник, грани которого – пятиугольники и треугольники.
Слайд 33Усеченный додекаэдр
С додекаэдром работы больше. Надо срезать двадцать вершин.
Грани усеченного додекаэдра
– треугольники и десятиугольники.
