- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к уроку геометрии Призма. Изображение призмы и построение ее сечений 11 класс. А.В. Погорелов.
Содержание
- 1. Презентация к уроку геометрии Призма. Изображение призмы и построение ее сечений 11 класс. А.В. Погорелов.
- 2. Призма многогранник, составленный из двух плоских
- 3. Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы,A1В1В2А2 , A2В2В3А3 – боковые грани призмы
- 4. Отрезки A1B1, A2B2, … , AnBn называются
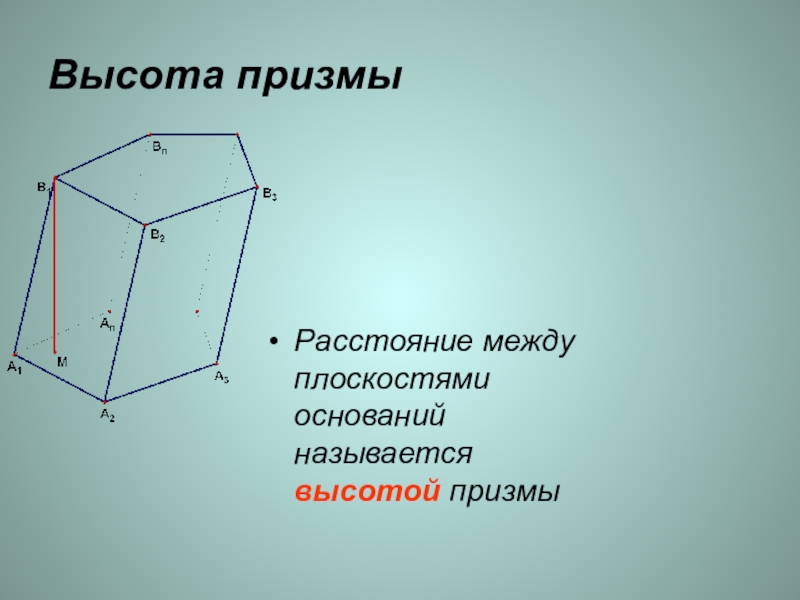
- 5. Расстояние между плоскостями оснований называется высотой призмы Высота призмы
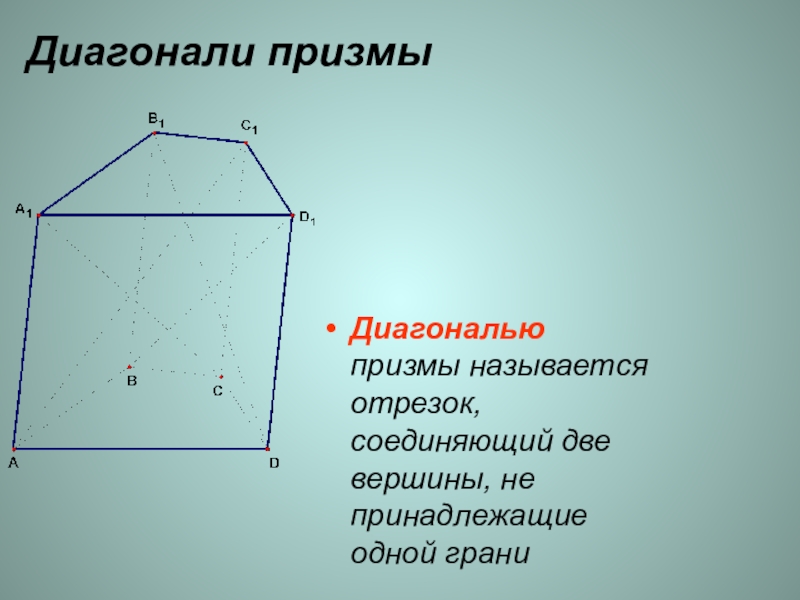
- 6. Диагонали призмыДиагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной грани
- 7. Призма называется с n-угольной призмой, если ее основания n – угольники
- 8. Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность состоит из параллелограммов
- 9. Призма называется прямой, если ее боковые ребра
- 10. Правильная призмаПрямая призма называется правильной, если её
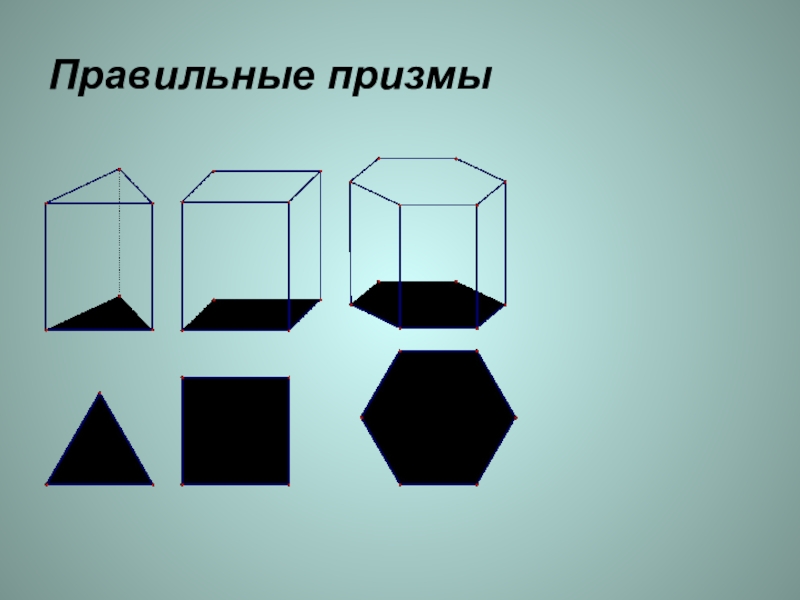
- 11. Правильные призмы
- 12. Сечения призмы
- 13. Диагональные сечения призмыСечения призмы плоскостями, проходящими через
- 14. Способы задания плоскости сечения:Двумя пересекающимися прямымиПрямой и
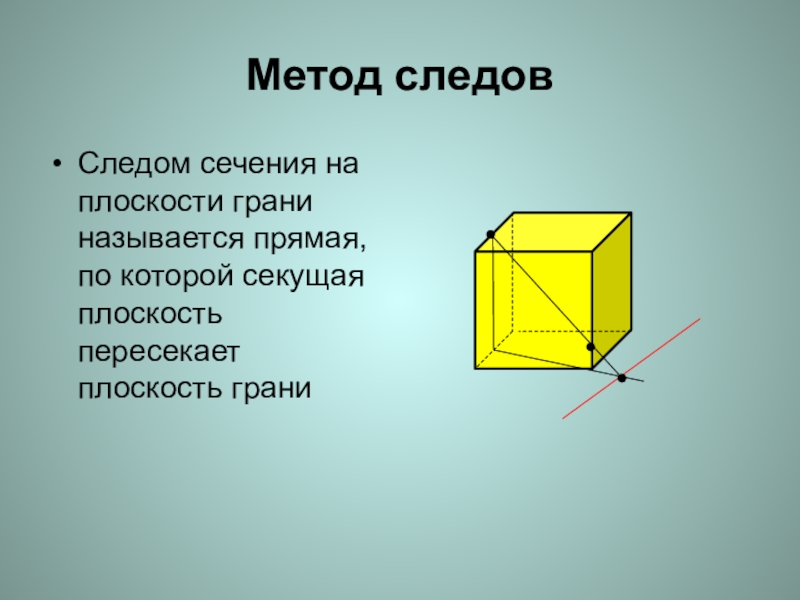
- 15. Метод следовСледом сечения на плоскости грани называется прямая, по которой секущая плоскость пересекает плоскость грани
- 16. ЗадачаПостроить сечение куба, проходящего через точки М, N, L
- 17. Задача Построить сечение куба, проходящего через точки М, N, К
- 18. Домашняя работаП.32, 33
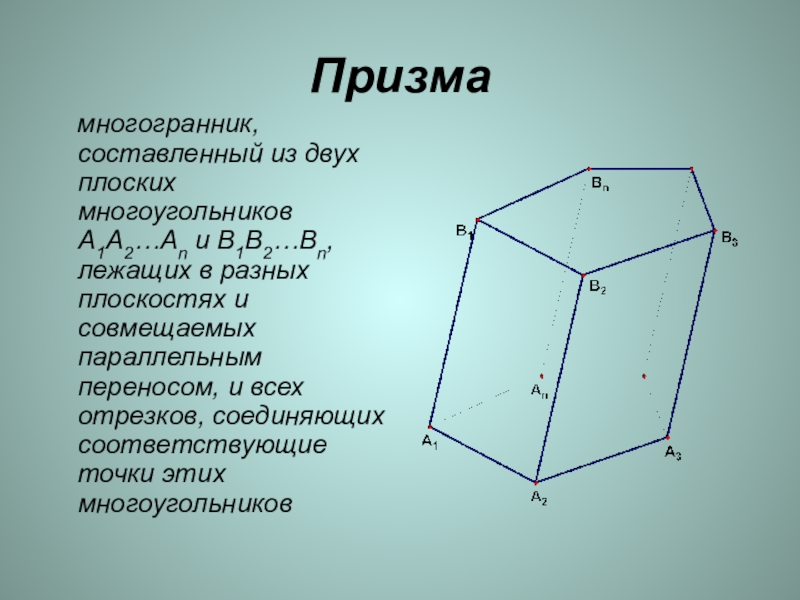
Призма многогранник, составленный из двух плоских многоугольников A1A2…An и B1B2…Bn, лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников
Слайд 2Призма
многогранник, составленный из двух плоских многоугольников A1A2…An и B1B2…Bn,
лежащих в разных плоскостях и совмещаемых параллельным переносом, и всех отрезков, соединяющих соответствующие точки этих многоугольников
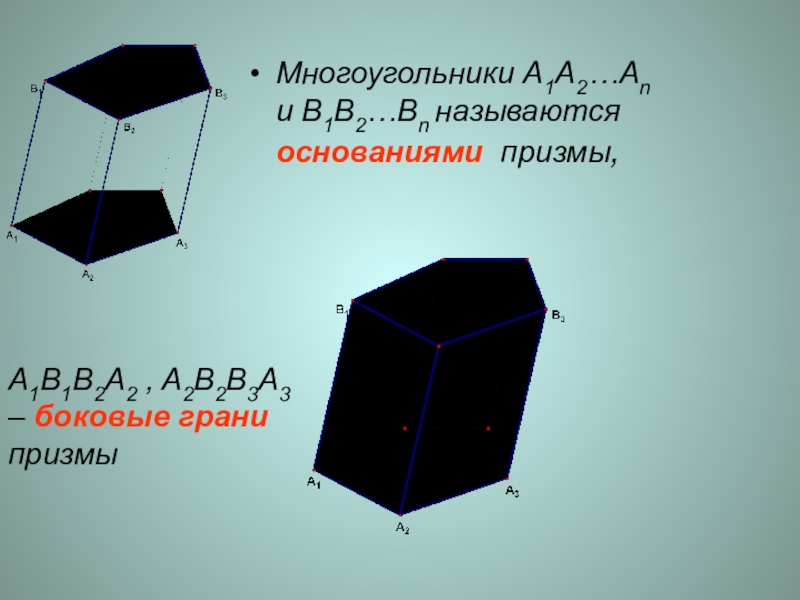
Слайд 3Многоугольники A1A2…An и B1B2…Bn называются основаниями призмы,
A1В1В2А2 , A2В2В3А3 – боковые
грани призмы
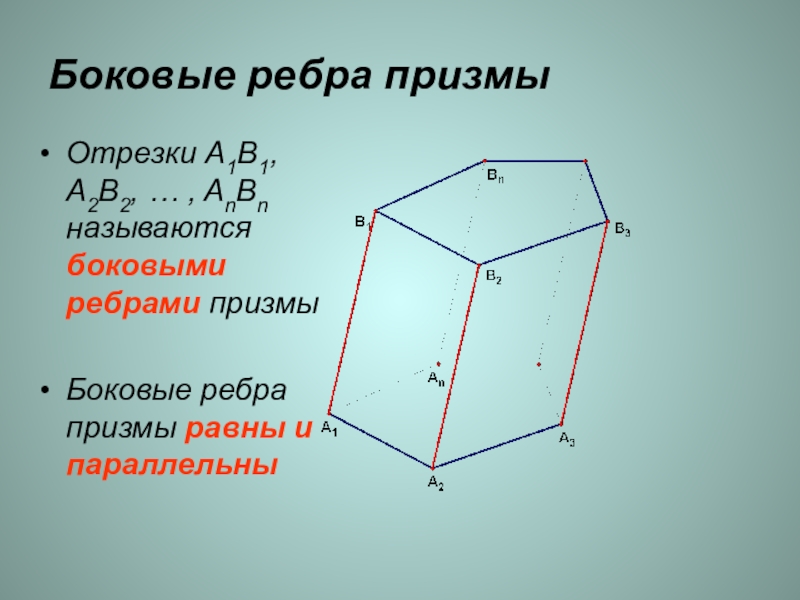
Слайд 4Отрезки A1B1, A2B2, … , AnBn называются боковыми ребрами призмы
Боковые ребра
призмы равны и параллельны
Боковые ребра призмы
Слайд 6Диагонали призмы
Диагональю призмы называется отрезок, соединяющий две вершины, не принадлежащие одной
грани
Слайд 8Поверхность призмы состоит из оснований и боковой поверхности. Боковая поверхность состоит
из параллелограммов
Слайд 9Призма называется прямой, если ее боковые ребра перпендикулярны основаниям.
Призма называется
наклонной, если ее боковые ребра не перпендикулярны основаниям.
Высота прямой призмы равна её боковому ребру
Высота прямой призмы равна её боковому ребру
Виды призм
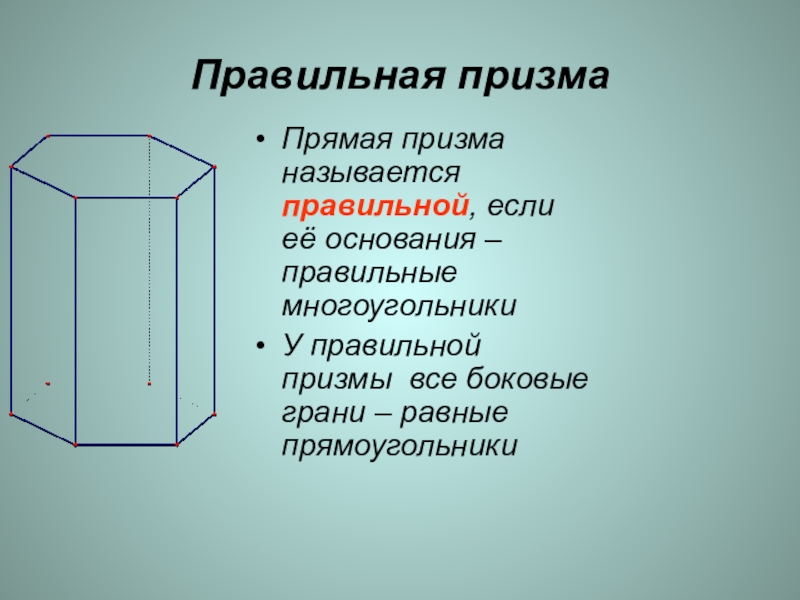
Слайд 10Правильная призма
Прямая призма называется правильной, если её основания – правильные многоугольники
У
правильной призмы все боковые грани – равные прямоугольники
Слайд 13Диагональные сечения призмы
Сечения призмы плоскостями, проходящими через два боковых ребра, не
принадлежащих одной грани, называются диагональными сечениями
Диагональные сечения призмы являются параллелограммами
Диагональные сечения призмы являются параллелограммами
Слайд 14Способы задания плоскости сечения:
Двумя пересекающимися прямыми
Прямой и не лежащей на ней
точкой
Тремя не лежащими на одной прямой точками
Двумя параллельными прямыми
Тремя не лежащими на одной прямой точками
Двумя параллельными прямыми
Слайд 15Метод следов
Следом сечения на плоскости грани называется прямая, по которой секущая
плоскость пересекает плоскость грани