- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме равенство прямоугольных треугольников
Содержание
- 1. Презентация по теме равенство прямоугольных треугольников
- 2. Введение Методы исследования:сбор материала;анализ; обобщение. Цель работы
- 3. Немного истории Математический папирус АхмесаЕгипетский треугольник
- 4. Треугольник – это геометрическаяфигура, состоящая из трёх
- 5. Свойства углов: – сумма острых углов прямоугольного
- 6. Для того, чтобы установить равенство треугольников, необходимо
- 7. Признак 1 – по двум катетамЕсли катеты
- 8. Признак 2 – по катету и прилежащему
- 9. Признак 3 – по гипотенузе и острому
- 10. Признак 4 – по гипотенузе и катетуЕсли
- 11. Теорема ПифагораЕсли гипотенуза и острый угол одного
- 12. Теорема ПифагораСАВДоказательство:Пусть ВС=а, АС=b, АВ=с На гипотенузе АВ построим квадрат со стороной с baсссс
- 13. Теорема ПифагораСАВДоказательство:На продолжении стороны АС отложим отрезок
- 14. Теорема ПифагораДоказательство:А так как ∠C=90º и CF=CK,
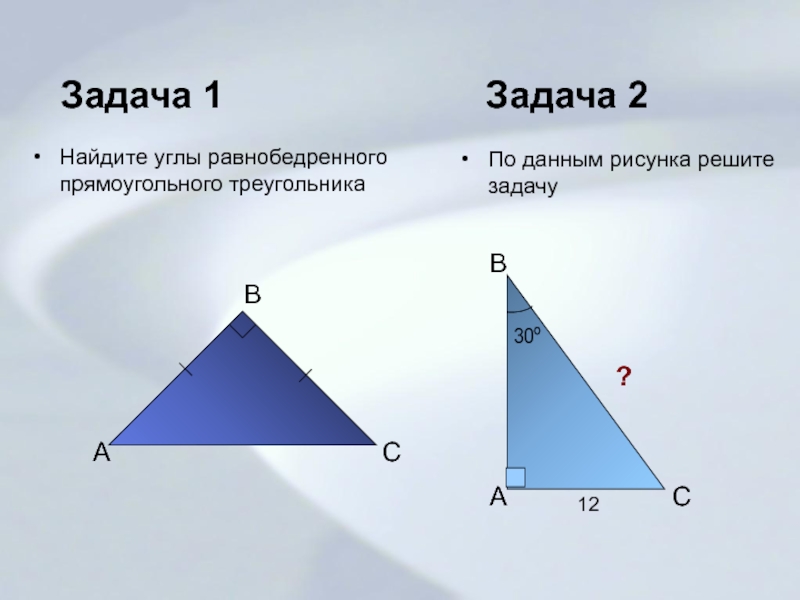
- 15. Задача 1Найдите углы равнобедренного прямоугольного треугольникаABC30º12?Задача 2По данным рисунка решите задачуBAC
- 16. Игра «Угадай»
- 17. Проверь себя 1 вариант
Слайд 2Введение
Методы исследования:
сбор материала;
анализ;
обобщение.
Цель работы :
Изучение и обобщение знаний
прямоугольном треугольнике
Практическая значимость:
при решении олимпиадных задач мне не хватает знаний
по геометрии;
хочу расширить свои знания, про признаки
прямоугольного треугольника.
Слайд 4Треугольник – это геометрическая
фигура, состоящая из трёх точек, не
лежащих на одной
соединяющих эти точки.
Если один из углов треугольника прямой,
то треугольник называется
прямоугольным.
Сторона прямоугольного треугольника,
лежащая против прямого угла, называется
гипотенузой, а две другие – катетами.
Определения
гипотенуза
катет
катет
Слайд 5Свойства углов:
– сумма острых углов прямоугольного треугольника равна 900;
–
половине гипотенузы, равен 300
– в равнобедренном прямоугольном
треугольнике острые углы равны по 450
Свойства сторон:
– катет всегда меньше гипотенузы
– катет, лежащий против угла в 300,
равен половине гипотенузы.
Свойства прямоугольного треугольника
гипотенуза
катет
катет
Слайд 6Для того, чтобы установить равенство треугольников, необходимо доказать равенство трех элементов,
катеты одного из них, равны катетам другого;
гипотенуза и острый угол одного из них равны гипотенузе и острому углу другого;
катет и острый угол одного из них равны катету и острому углу другого.
Признаки равенства прямоугольных
треугольников
гипотенуза
катет
катет
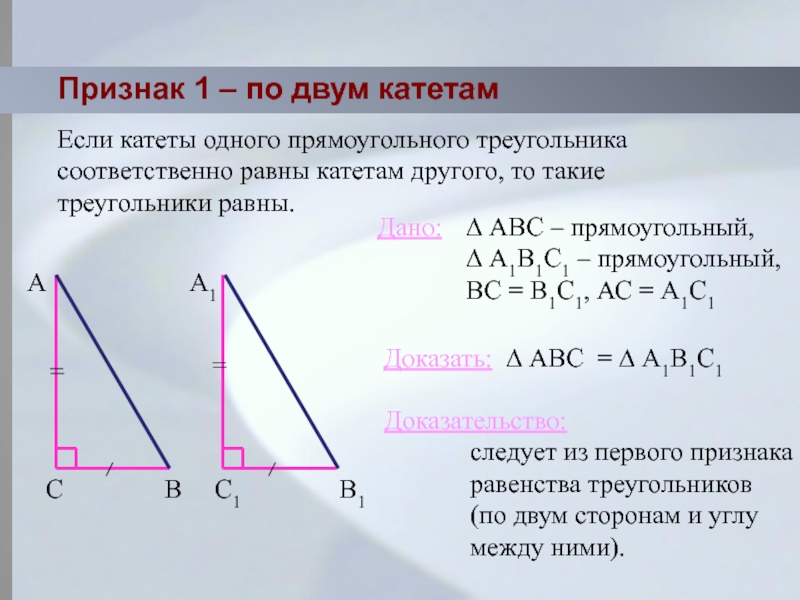
Слайд 7Признак 1 – по двум катетам
Если катеты одного прямоугольного треугольника
соответственно
треугольники равны.
∆ АВС – прямоугольный,
∆ А1В1С1 – прямоугольный,
ВС = В1С1, АС = А1С1
Дано:
С
С1
А
А1
В
В1
∆ АВС = ∆ А1В1С1
Доказать:
следует из первого признака равенства треугольников
(по двум сторонам и углу между ними).
Доказательство:
Слайд 8Признак 2 – по катету и прилежащему углу
Если катет и прилежащий
Дано:
С
С1
А
А1
В
В1
∆ АВС = ∆ А1В1С1
Доказать:
следует из второго признака равенства треугольников
(по стороне и прилежащим к ней углам)
Доказательство:
∆ АВС – прямоугольный,
∆ А1В1С1 – прямоугольный,
АС = А1С1 , ∠А=∠А1
Слайд 9Признак 3 – по гипотенузе и острому углу
Если гипотенуза и острый
Дано:
С
С1
А
А1
В
В1
∆ АВС = ∆ А1В1С1
Доказать:
Доказательство:
∆ АВС – прямоугольный,
∆ А1В1С1 – прямоугольный,
АВ = А1В1 , ∠А=∠А1
т.к. сумма острых углов прямоугольного треугольника равна 90°, то два других острых угла также равны, поэтому треугольники равны по второму признаку равенства треугольников (по стороне и прилежащим к ней углам).
Слайд 10Признак 4 – по гипотенузе и катету
Если гипотенуза и острый угол
Дано:
С
С1
А
А1
В
В1
∆ АВС = ∆ А1В1С1
Доказать:
Доказательство:
∆ АВС – прямоугольный,
∆ А1В1С1 – прямоугольный,
АВ = А1В1 , АС = А1С1 .
Наложим ∆ А1В1С1 на треугольник ∆ АВС. Т.к. АС = А1С1 и АВ = А1В1, то они при наложении совпадут. Тогда вершина А1 совместиться с вершиной А. Но и тогда и вершины В1 и В также совместятся. Следовательно, треугольники равны.
Слайд 11Теорема Пифагора
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны
Дано:
С
А
В
АВ2= ВС2+АС2
Доказать:
Доказательство:
∆ АВС, ∠С=90°
Наложим ∆ А1В1С1 на треугольник ∆ АВС. Т.к. АС = А1С1 и АВ = А1В1, то они при наложении совпадут. Тогда вершина А1 совместиться с вершиной А. Но и тогда и вершины В1 и В также совместятся. Следовательно, треугольники равны.
b
a
с
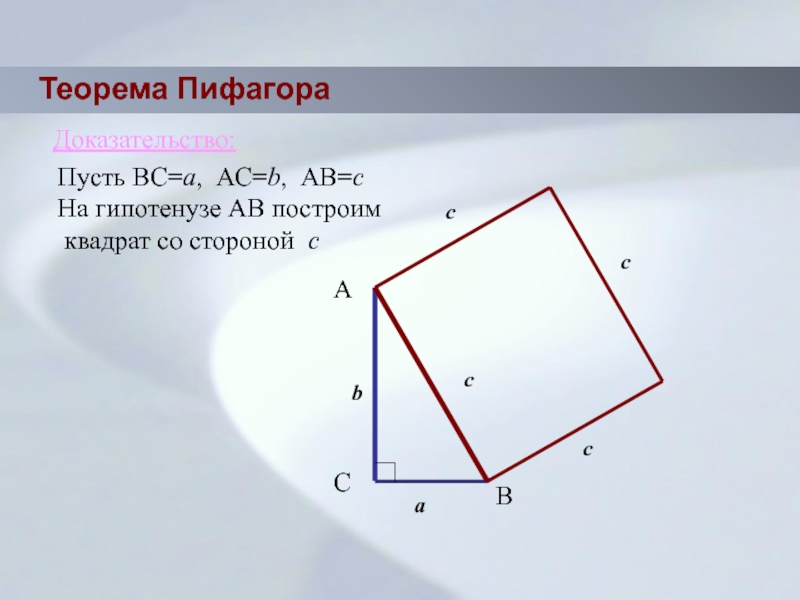
Слайд 12Теорема Пифагора
С
А
В
Доказательство:
Пусть ВС=а, АС=b, АВ=с
На гипотенузе АВ построим
квадрат со
b
a
с
с
с
с
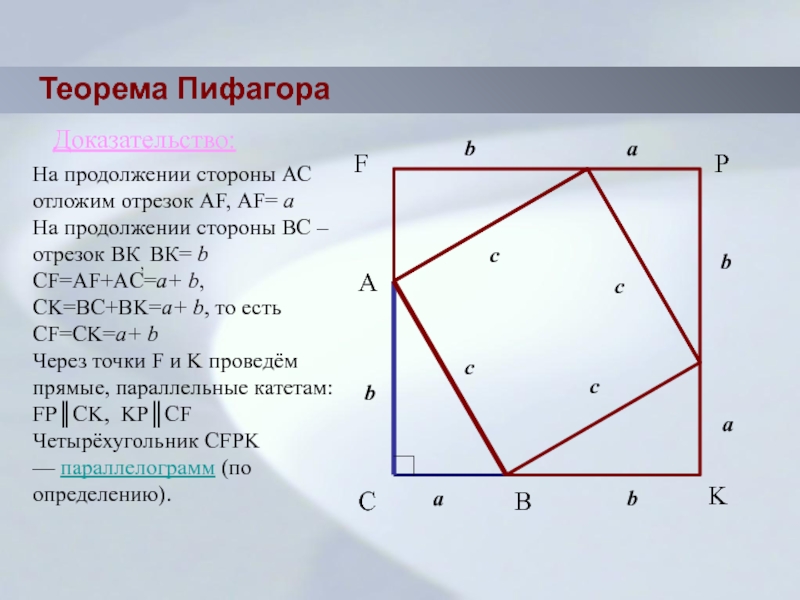
Слайд 13Теорема Пифагора
С
А
В
Доказательство:
На продолжении стороны АС отложим отрезок АF, АF= a
На продолжении
CF=AF+AC=a+ b, CK=BC+BK=a+ b, то есть CF=CK=a+ b
Через точки F и K проведём прямые, параллельные катетам:
FP║CK, KP║CF
Четырёхугольник CFPK — параллелограмм (по определению).
b
a
с
с
с
с
F
K
P
a
a
b
b
b
Слайд 14Теорема Пифагора
Доказательство:
А так как ∠C=90º и CF=CK, то CFPK — квадрат
Так как площадь квадрата равна квадрату его стороны, то S CFPK = (a+b)2
С другой стороны, площадь CFPK равна сумме площадей четырёх прямоугольных треугольников с катетами b и c и квадрата со стороной c.
Площадь прямоугольного треугольника равны половине произведения его катетов:
S ∆ АВС=1/2 ВС·АС=1/2 а b
площадь квадрата со стороной c равна c².
Следовательно, S CFPK =4·1/2 а b+с2= 2 а b+с2
Приравняем правые части формул площади CFPK: 2 а b+с2= (a+b)2
Имеем: 2 а b+с2= a2 +2 а b+ b2
После упрощения получаем: c²= a2 +b 2
то есть, АВ2=ВС2+АС2
Что и требовалось доказать.
Поскольку в прямоугольном треугольнике катеты чаще всего обозначаются как a и b , а гипотенуза — как c, то формула теоремы Пифагора обычно записывается именно так: c² = a2 + b 2