- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Симметрия в пространстве, геометрия 10 класс
Содержание
- 1. Симметрия в пространстве, геометрия 10 класс
- 2. «Мир полон удивительной красотыи благородства, которые вы
- 3. РЕБУС
- 4. Мы живем в очень красивом игармоничном мире.
- 5. Слово “симметрия” в переводе с греческогозвучит
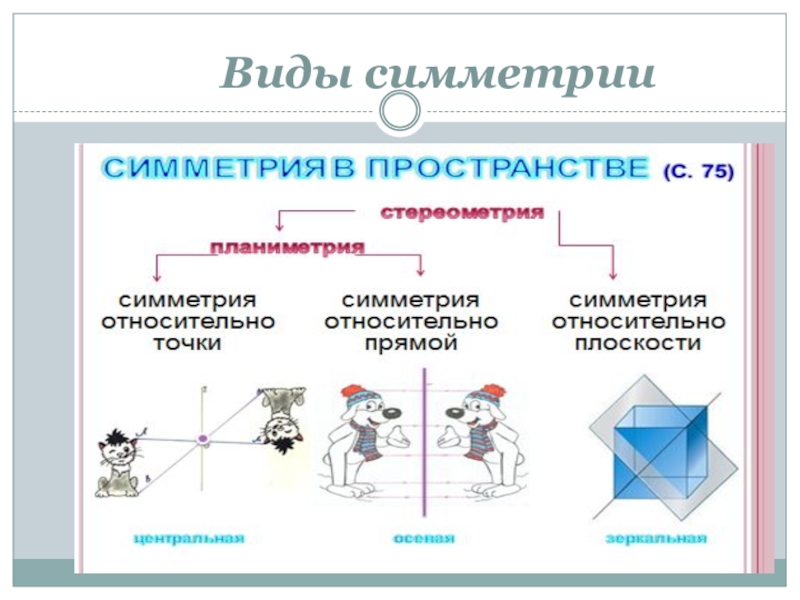
- 6. Виды симметрии
- 7. СИММЕТРИЯ В ПРОСТРАНСТВЕ«Симметрия … есть идея, с
- 8. СИММЕТРИЯ В ПРОСТРАНСТВЕТочки А и А1 называются
- 9. СИММЕТРИЯ В ПРОСТРАНСТВЕ«Что может быть более похоже
- 10. Точки А и А1 называются симметричными относительно
- 11. Точки А и А1 называются симметричными относительно
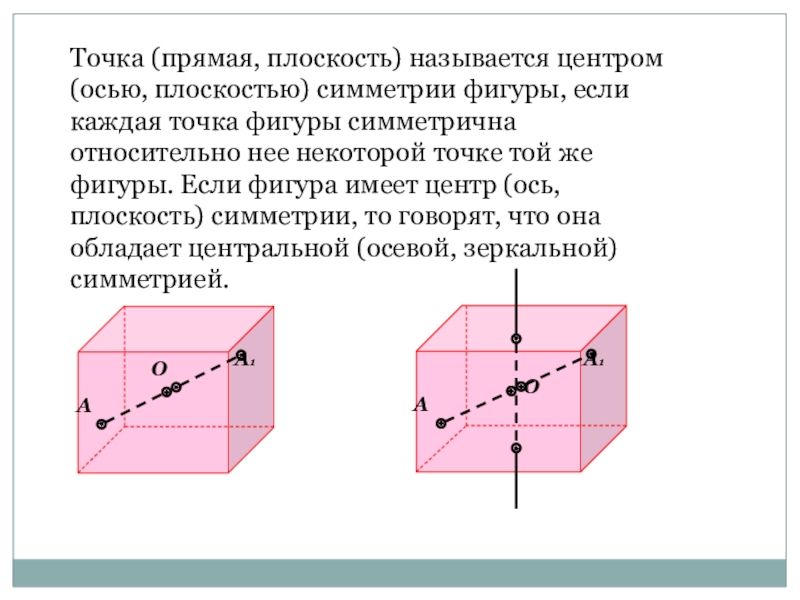
- 12. Точка (прямая, плоскость) называется центром (осью, плоскостью)
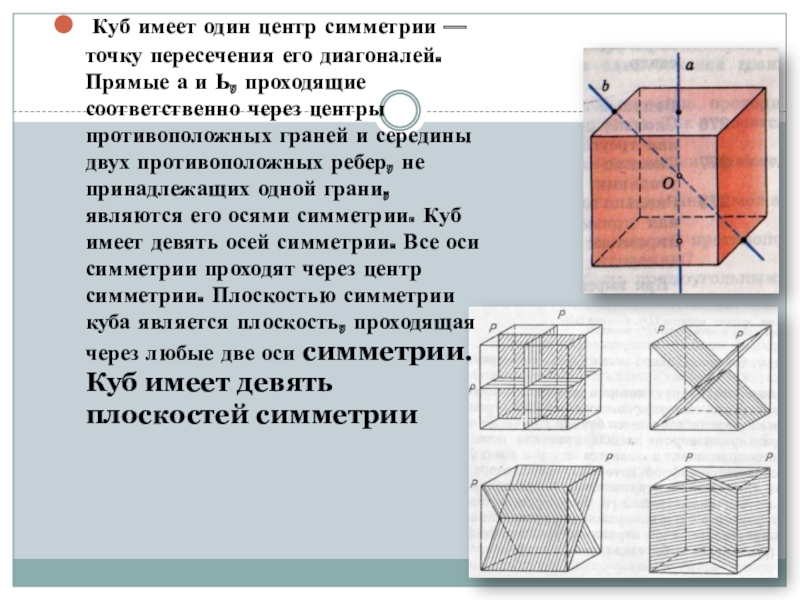
- 13. Куб имеет один центр симметрии —
Слайд 1
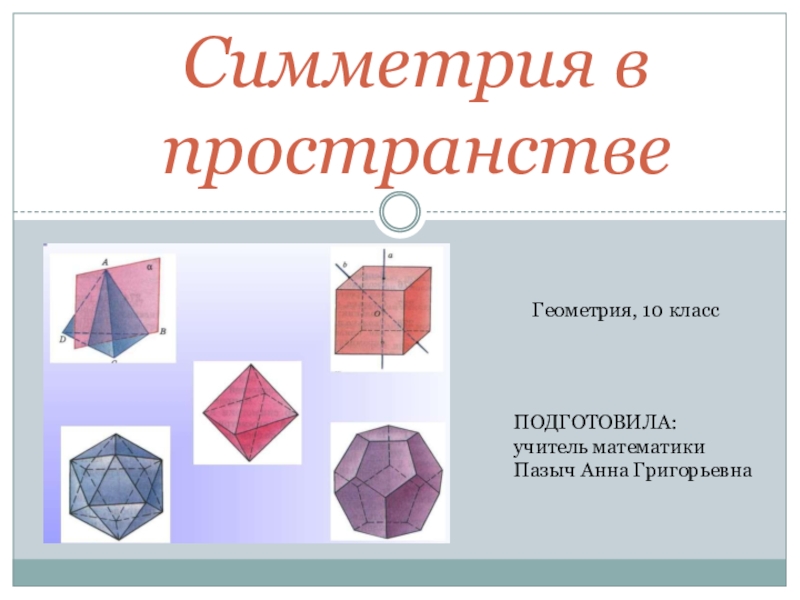
Симметрия в пространстве
ПОДГОТОВИЛА:
учитель математики
Пазыч Анна Григорьевна
Геометрия, 10 класс
Слайд 2«Мир полон удивительной красоты
и благородства, которые вы должны
открывать, прежде всего, сами.
Нужно
готовиться к встрече с чудом».
А. Н. Колмогорова
Слайд 4Мы живем в очень красивом и
гармоничном мире. Нас окружают
предметы, которые радуют
Например, бабочка, кленовый лист,
снежинка, берёза под окном. Посмотрите,
как они прекрасны. Вы обращали на это
внимание? Сегодня мы с вами прикоснемся
к этому прекрасному математическому
явлению – симметрии. Познакомимся с
понятием осевой, центральной и зеркальной
симметрией. Будем учиться строить и
определять симметричные относительно оси,
центра и плоскости фигуры.
Слайд 5 Слово “симметрия” в переводе с греческого
звучит как “гармония”, которая означает
соразмерность, пропорциональность, одинаковость
в расположении частей.
Понятие симметрии проходит через всю историю
человечества. Оно встречается у истоков
человеческого знания. Возникло оно в связи с
изучением живого организма, а именно человека.
Ещё V веке до н.э. использовали симметрию в
архитектуре. Древним храмам, башням
средневековых замков, да и современным зданиям
она придает гармоничность, законченность.
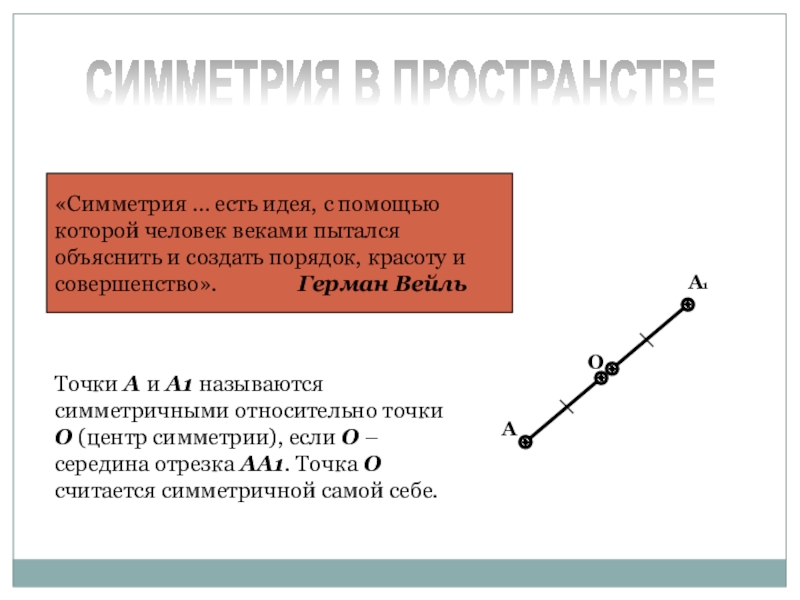
Слайд 7СИММЕТРИЯ В ПРОСТРАНСТВЕ
«Симметрия … есть идея, с помощью
которой человек веками
объяснить и создать порядок, красоту и
совершенство». Герман Вейль
А
А1
Точки А и А1 называются симметричными относительно точки О (центр симметрии), если О – середина отрезка АА1. Точка О считается симметричной самой себе.
Слайд 8СИММЕТРИЯ В ПРОСТРАНСТВЕ
Точки А и А1 называются симметричными относительно прямой (ось
А1
Слайд 9СИММЕТРИЯ В ПРОСТРАНСТВЕ
«Что может быть более похоже на мою
руку или
отражение в зеркале? И все же руку,
которую я вижу в зеркале, нельзя поставить
на место постоянной руки…»
Иммануил Кант
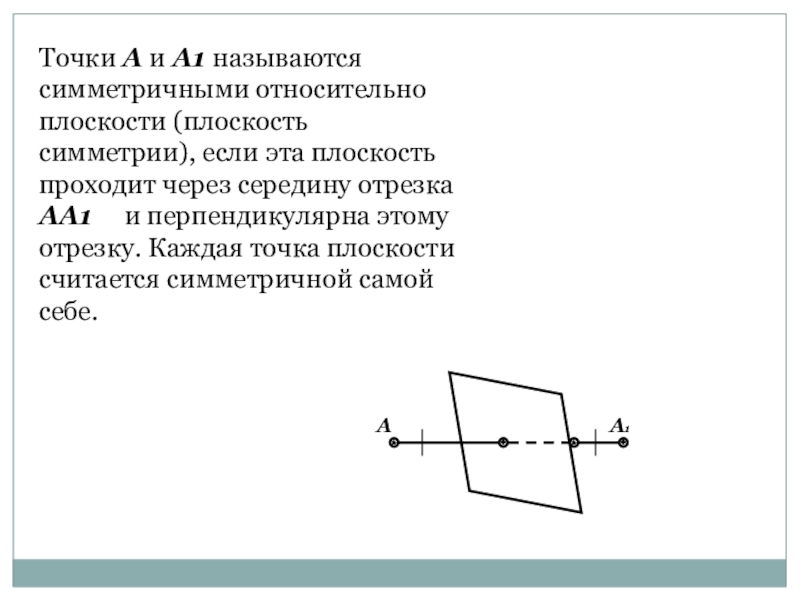
Точки А и А1 называются симметричными относительно плоскости (плоскость симметрии), если эта плоскость проходит через середину отрезка АА1 и перпендикулярна этому отрезку. Каждая точка плоскости считается симметричной самой себе.