- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Построение сечений в параллелепипеде
Содержание
- 1. Построение сечений в параллелепипеде
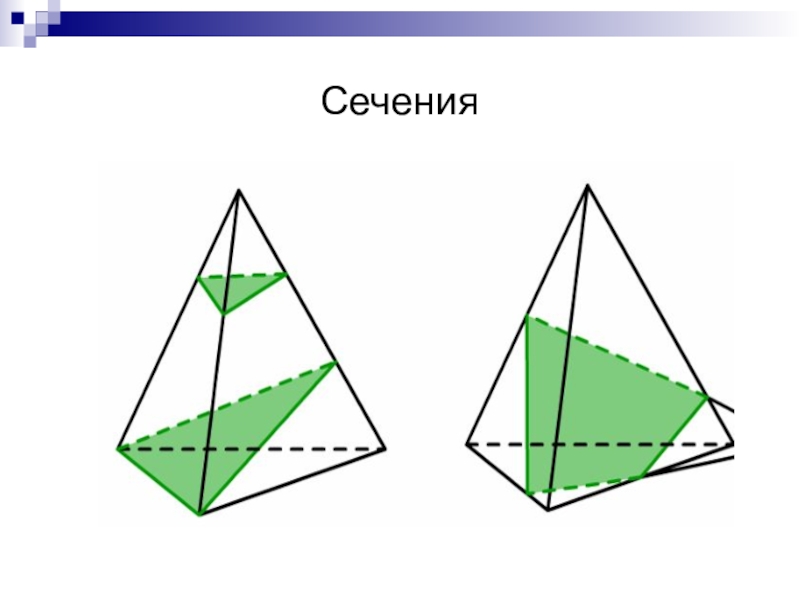
- 2. Сечения
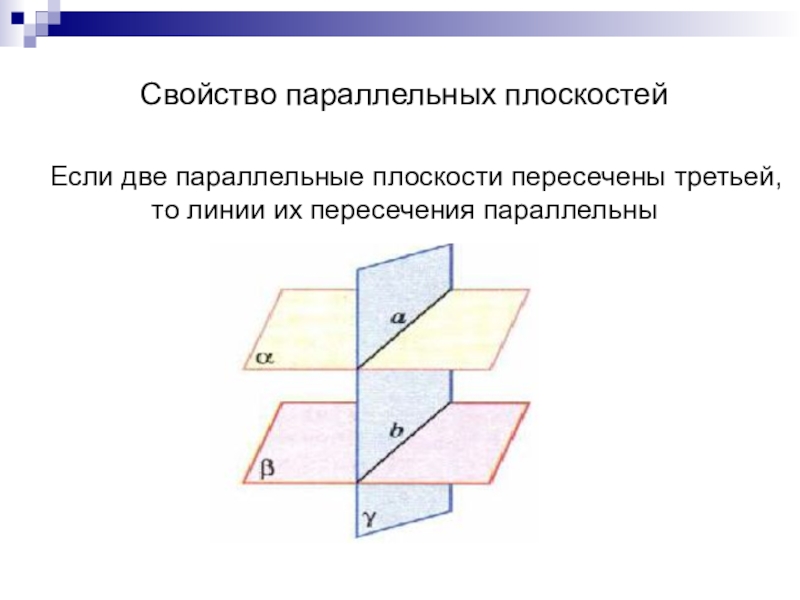
- 3. Свойство параллельных плоскостейЕсли две параллельные плоскости пересечены третьей, то линии их пересечения параллельны
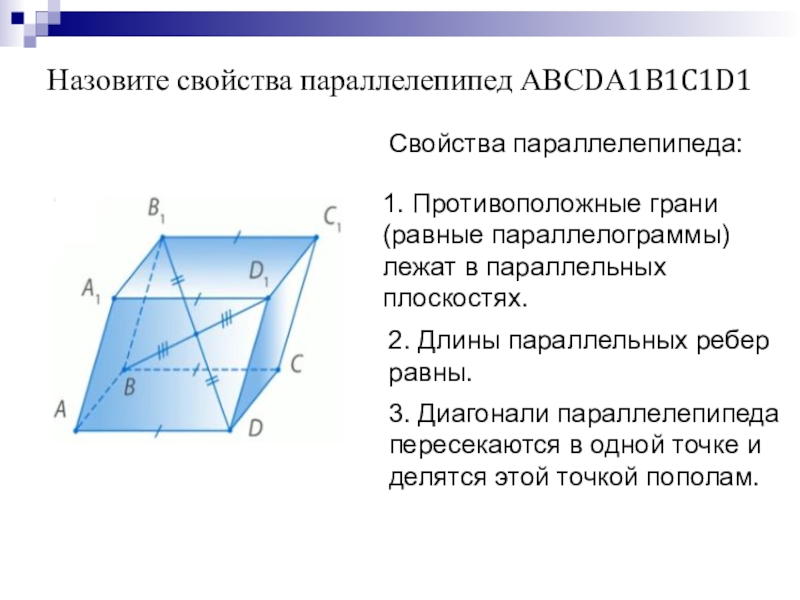
- 4. Назовите свойства параллелепипед АВСDА1B1C1D1Свойства параллелепипеда:1. Противоположные грани
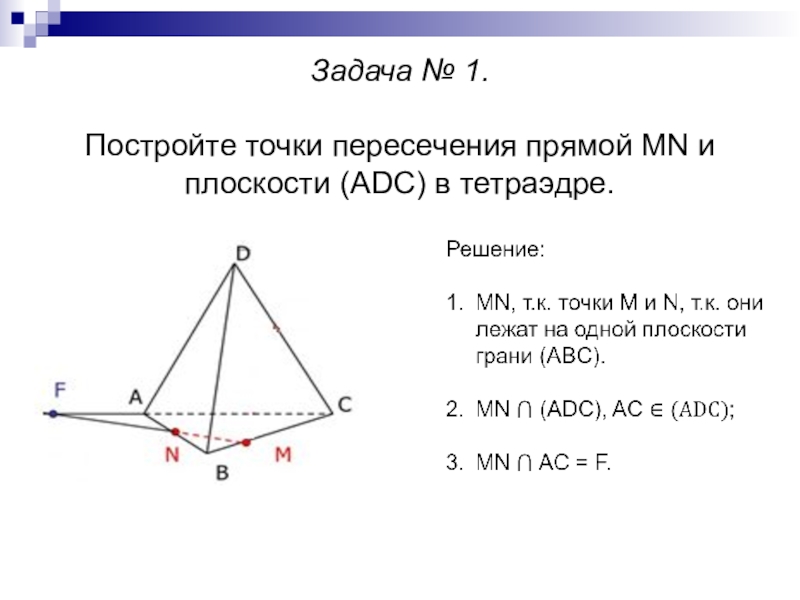
- 5. Задача № 1. Постройте точки пересечения прямой MN и плоскости (ADC) в тетраэдре.
- 6. Алгоритм построения точки пересечения прямой и плоскостиДля
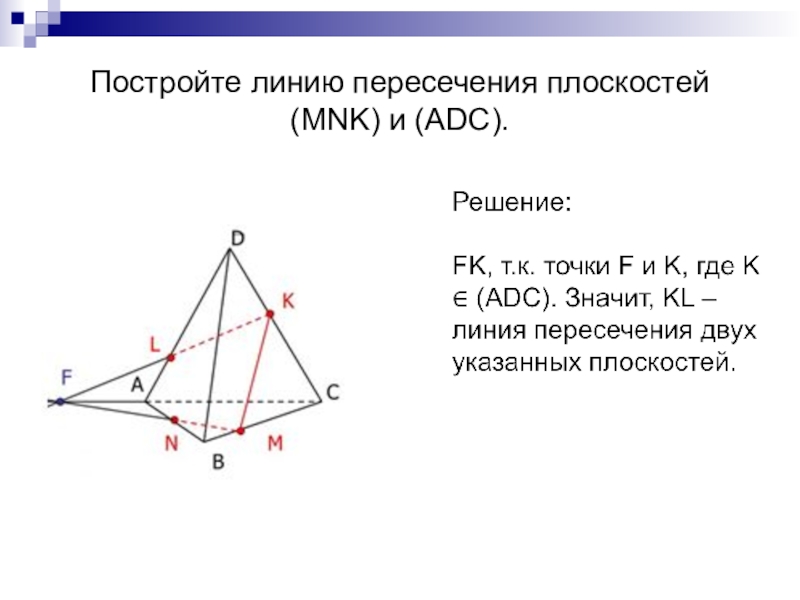
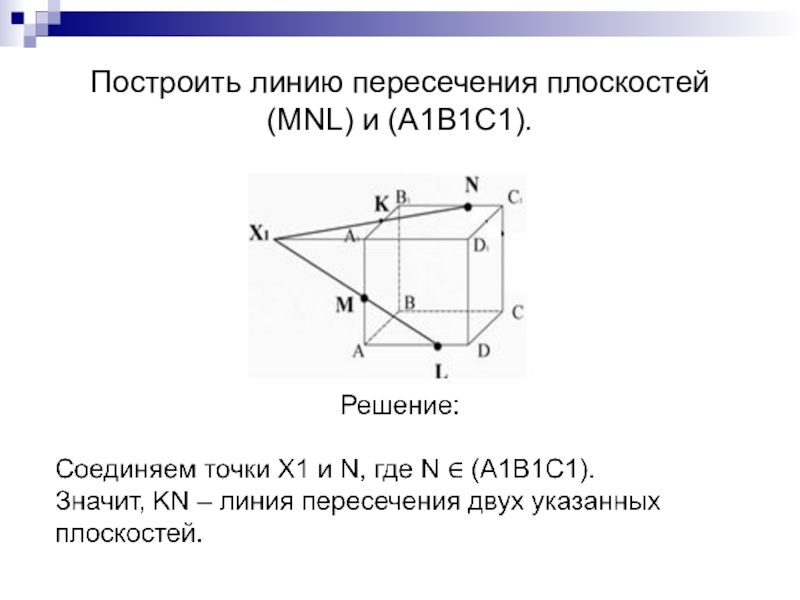
- 7. Постройте линию пересечения плоскостей (MNK) и (ADC).
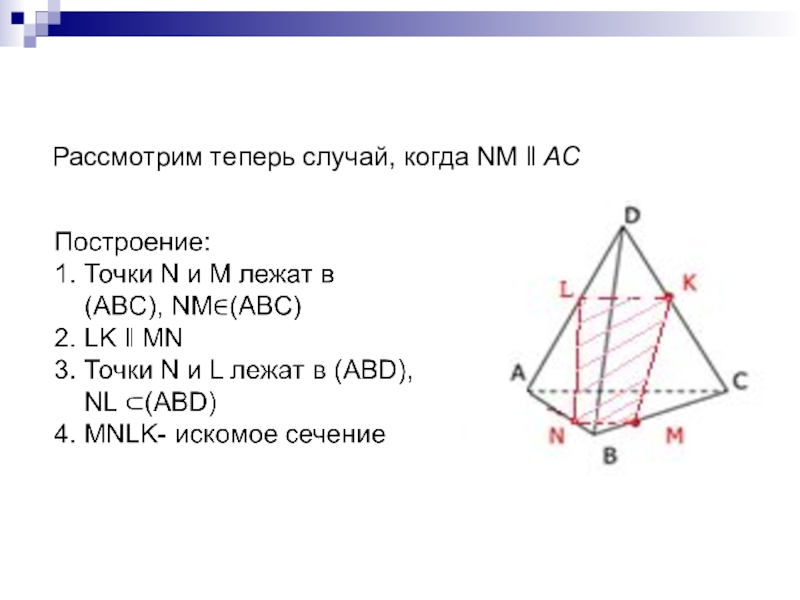
- 8. Рассмотрим теперь случай, когда NM ‖ AC
- 9. Алгоритм построения точки пересечения двух плоскостейДля построения
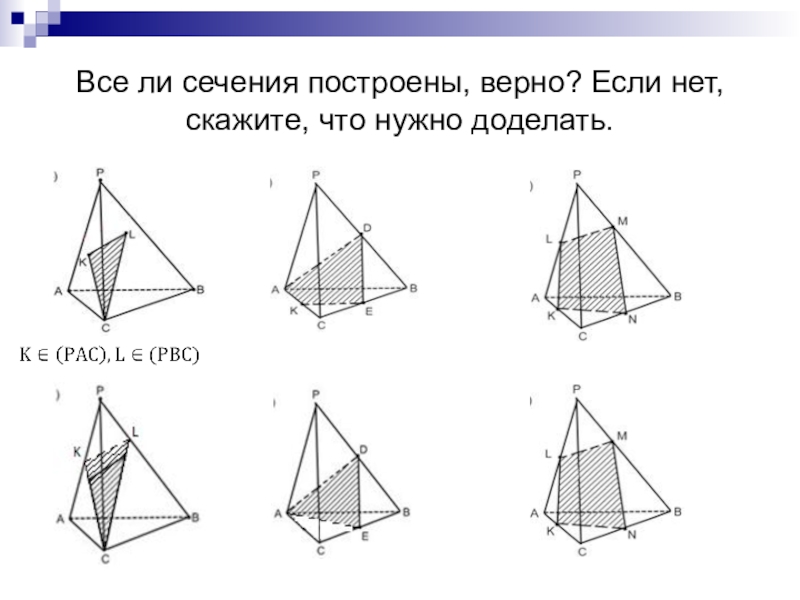
- 10. Все ли сечения построены, верно? Если нет, скажите, что нужно доделать.
- 11. Тема урока. «Построение сечений параллелепипеда плоскостью».
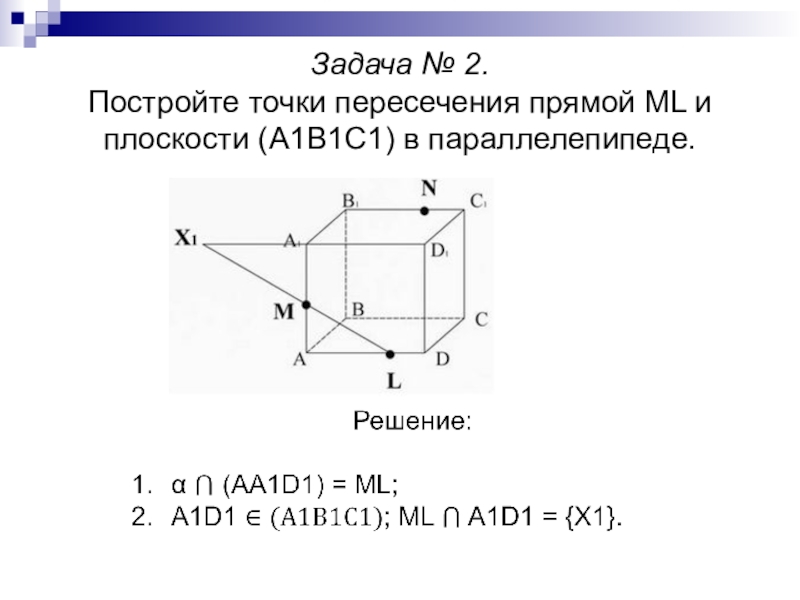
- 12. Задача № 2. Постройте точки пересечения прямой ML и плоскости (A1B1C1) в параллелепипеде.
- 13. Построить линию пересечения плоскостей (MNL) и (A1B1C1).
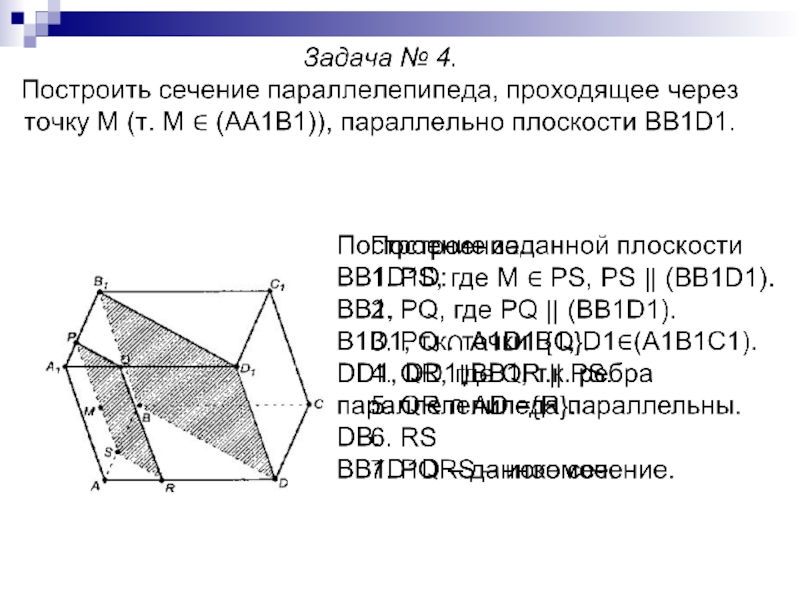
- 14. Задача № 3. Дан параллелепипед АВСDА’B’C’D’ и
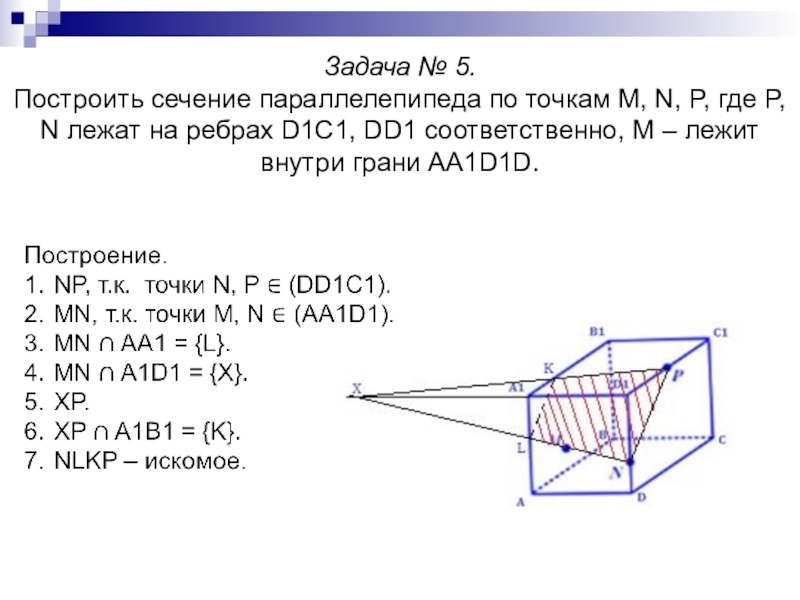
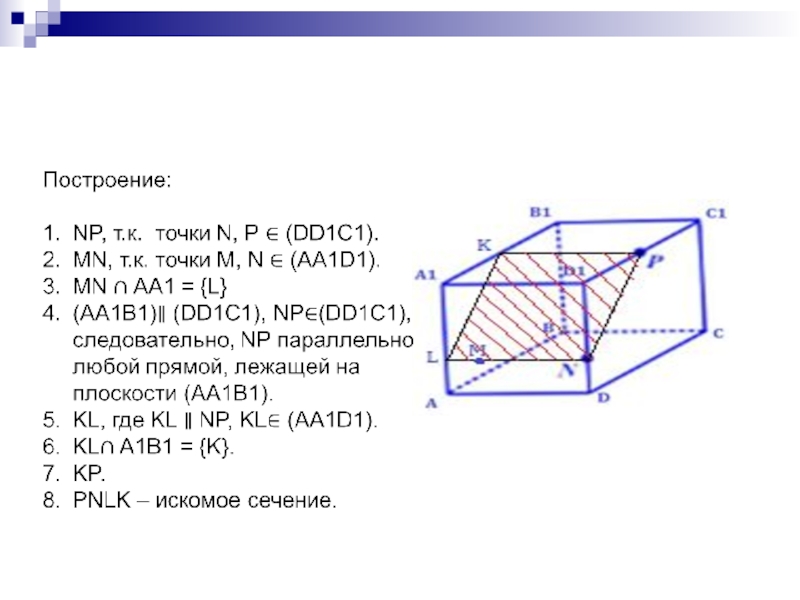
- 15. Задача № 5. Построить сечение параллелепипеда по
- 16.
- 17.
- 18. Задача 6. Построить сечение параллелепипеда по
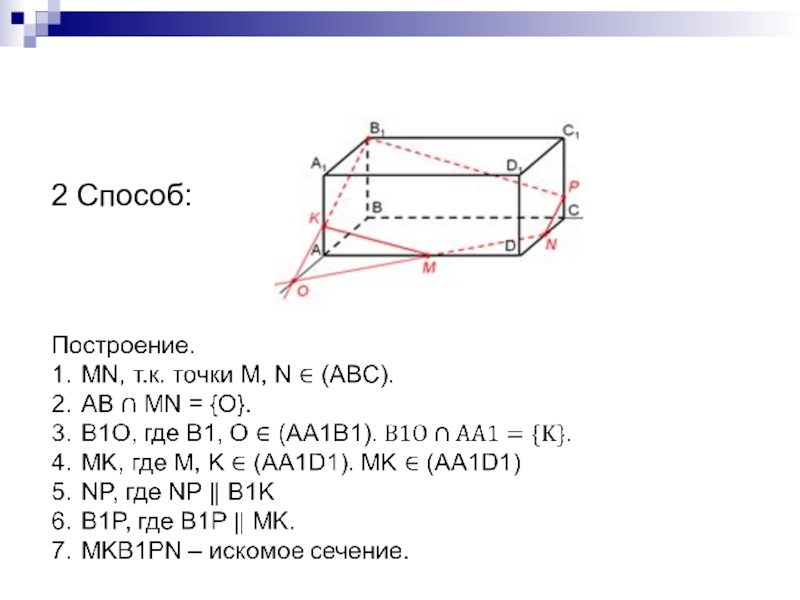
- 19. 2 Способ:
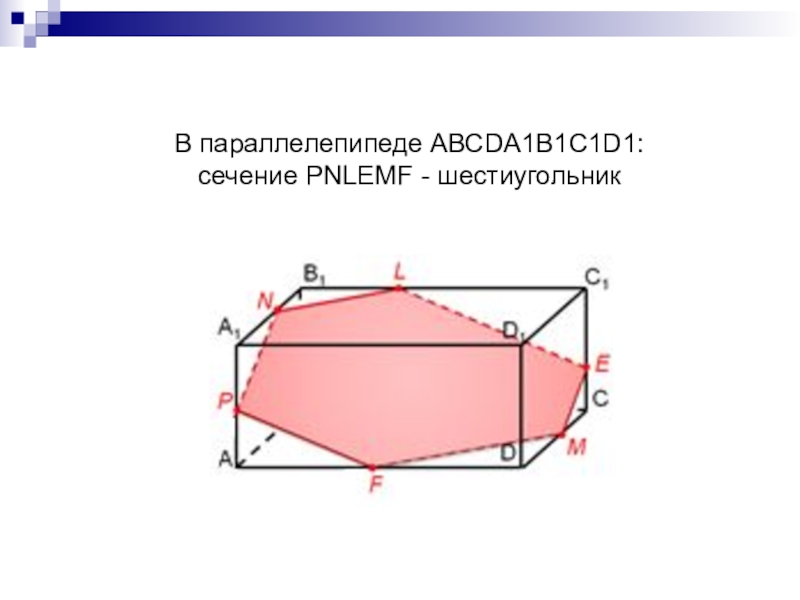
- 20. В параллелепипеде ABCDA1B1C1D1: сечение PNLEMF - шестиугольник
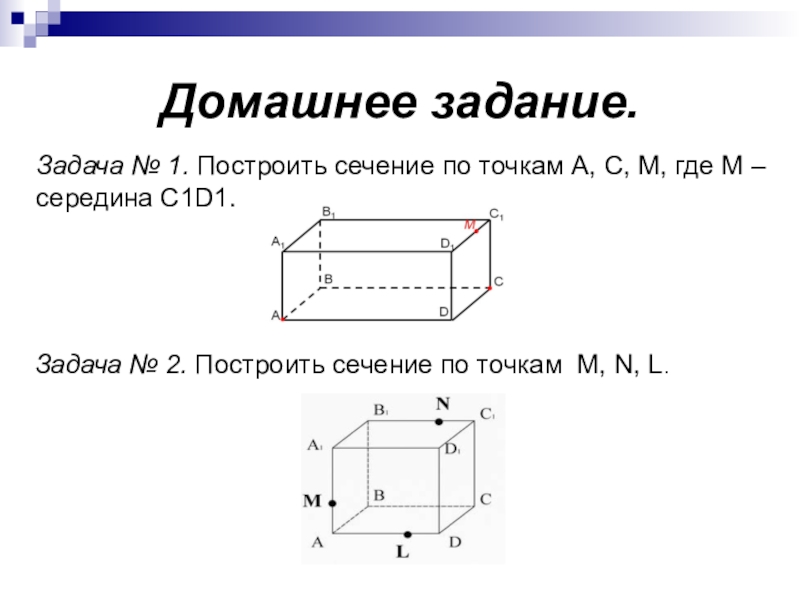
- 21. Домашнее задание.Задача № 1. Построить сечение по
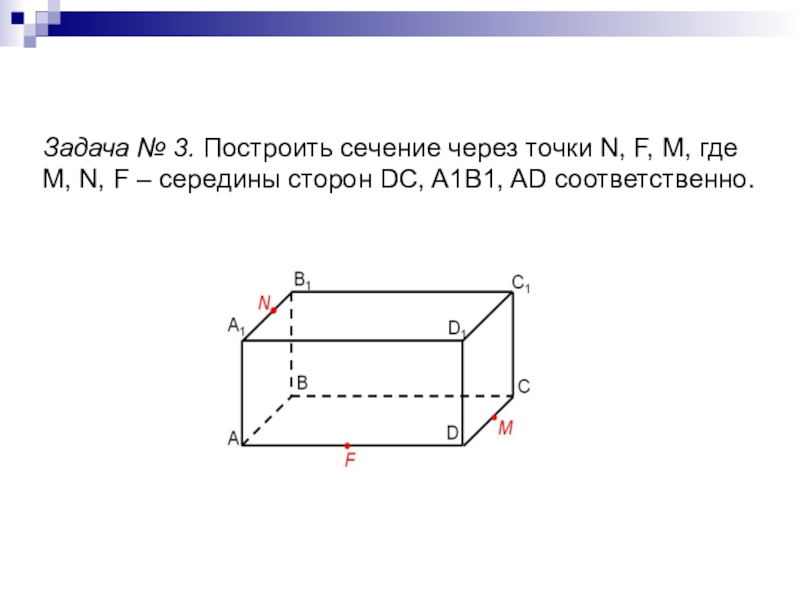
- 22. Задача № 3. Построить сечение через точки
Сечения
Слайд 1Построение сечений параллелепипеда плоскостью
Выполнила: студентка ФЕМиКН группы МП–10
Цапурина Любовь
Слайд 3Свойство параллельных плоскостей
Если две параллельные плоскости пересечены третьей, то линии их
пересечения параллельны
Слайд 4Назовите свойства параллелепипед АВСDА1B1C1D1
Свойства параллелепипеда:
1. Противоположные грани (равные параллелограммы) лежат в
параллельных плоскостях.
2. Длины параллельных ребер равны.
3. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Слайд 6Алгоритм построения точки пересечения прямой и плоскости
Для построения точки пересечения прямой
и плоскости надо:
найти в данной плоскости прямую, лежащую с данной прямой в какой либо другой плоскости;
построить точку пересечения этих прямых.
найти в данной плоскости прямую, лежащую с данной прямой в какой либо другой плоскости;
построить точку пересечения этих прямых.
Слайд 9Алгоритм построения точки пересечения двух плоскостей
Для построения линии пересечения двух плоскостей
нужно:
в одной плоскости найти две точки, принадлежащих другой плоскости
в одной плоскости найти две точки, принадлежащих другой плоскости
Слайд 14Задача № 3. Дан параллелепипед АВСDА’B’C’D’ и точки M, N, K на
ребрах AA’, A’D’, A’B’ соответственно. Постройте сечения параллелепипеда плоскостью MNK.
Построение.
MN, т.к. точки M и N лежат на одной пл. (AA’D’)
KN, т.к. точки K и N лежат на одной пл. (A’B’C’)
MK, т.к. точки M и K лежат на одной пл. (AA’B’)
(MNK) – искомое сечение.
Слайд 15Задача № 5. Построить сечение параллелепипеда по точкам M, N, P, где
P, N лежат на ребрах D1C1, DD1 соответственно, M – лежит внутри грани AA1D1D.
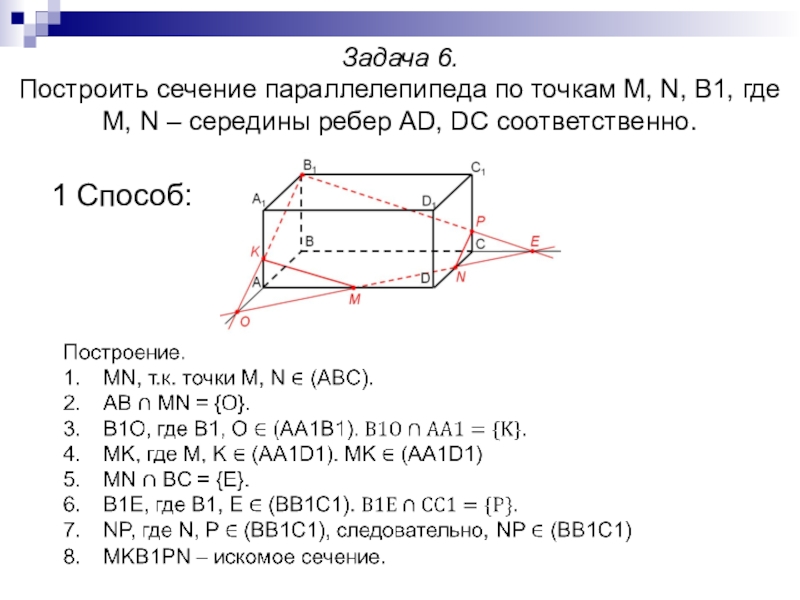
Слайд 18Задача 6. Построить сечение параллелепипеда по точкам M, N, B1, где
M, N – середины ребер AD, DC соответственно.
1 Способ:
Слайд 21Домашнее задание.
Задача № 1. Построить сечение по точкам A, C, M,
где M – середина C1D1.
Задача № 2. Построить сечение по точкам M, N, L.
Слайд 22Задача № 3. Построить сечение через точки N, F, M, где
M, N, F – середины сторон DC, A1B1, AD соответственно.
