- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Векторы в пространстве
Содержание
- 1. Векторы в пространстве
- 2. Определение вектора в пространствеВектор – направленный отрезок.Координаты
- 3. !
- 4. Действия над векторами в пространстве СЛОЖЕНИЕУМНОЖЕНИЕ НА ЧИСЛОСКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
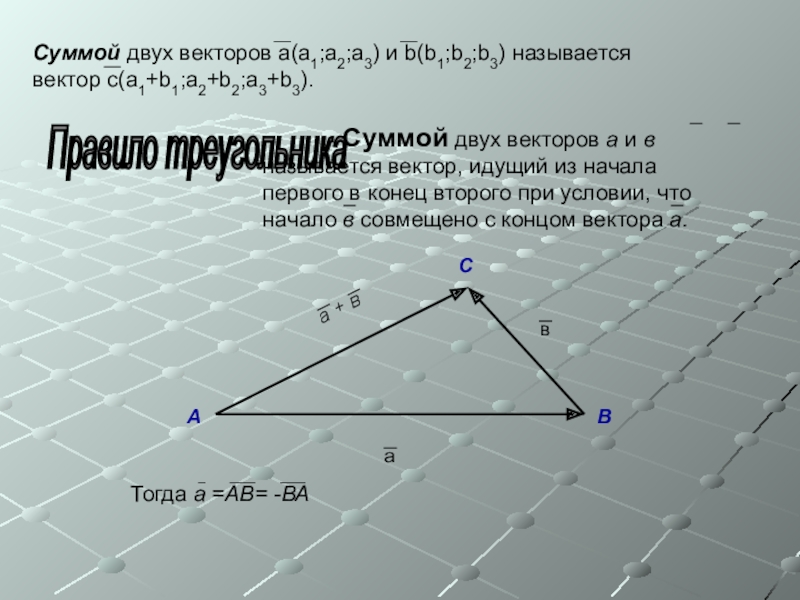
- 5. Правило треугольника АВС
- 6. Произведением вектора а(а1;а2;а3) на число λ называется вектор λа=(λа1; λа2; λа3)УТВЕРЖДЕНИЯ:
- 7. Скалярное произведение векторов Скалярное произведение векторов равно
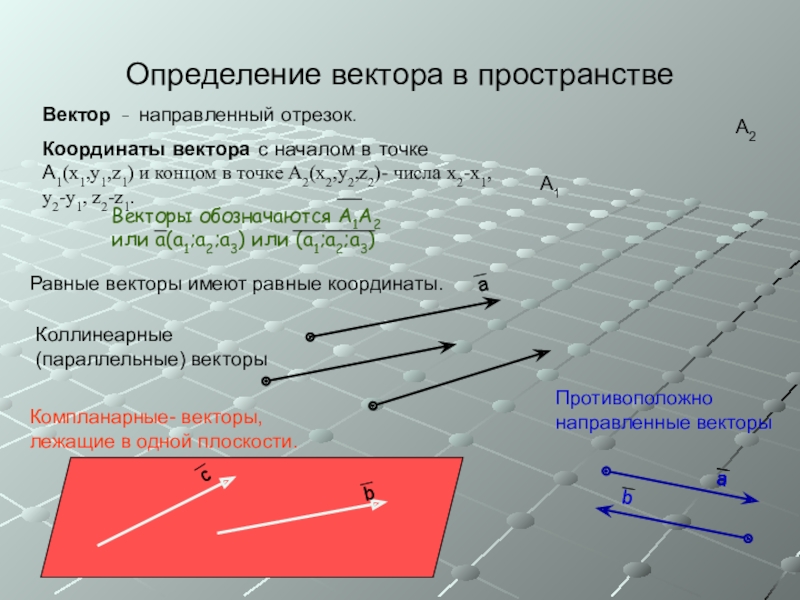
Определение вектора в пространствеВектор – направленный отрезок.Координаты вектора с началом в точке А1(x1,y1,z1) и концом в точке А2(x2,y2,z2)- числа x2-x1, y2-y1, z2-z1.А1А2Равные векторы имеют равные координаты.Коллинеарные (параллельные) векторыПротивоположно направленные векторы
Слайд 2Определение вектора в пространстве
Вектор – направленный отрезок.
Координаты вектора с началом в
точке А1(x1,y1,z1) и концом в точке А2(x2,y2,z2)- числа x2-x1, y2-y1, z2-z1.
А1
А2
Равные векторы имеют равные координаты.
Коллинеарные (параллельные) векторы
Противоположно направленные векторы
Слайд 6Произведением вектора а(а1;а2;а3) на число λ называется вектор λа=(λа1; λа2; λа3)
УТВЕРЖДЕНИЯ:
Слайд 7Скалярное произведение векторов
Скалярное произведение векторов равно произведению их абсолютных величин
на косинус угла между векторами, т. е.
СВОЙСТВА: