- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Четырехугольники
Содержание
- 1. Презентация по геометрии на тему Четырехугольники
- 2. Какая геометрическая фигура называется треугольником?Элементы треугольникаВиды треугольников,
- 3. Рассмотрим фигуру, состоящую из четырех точек
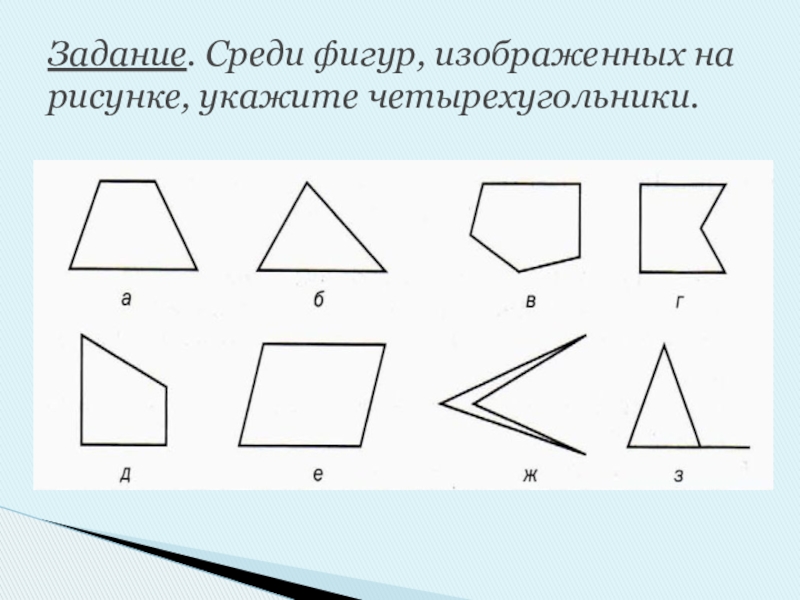
- 4. Задание. Среди фигур, изображенных на рисунке, укажите четырехугольники.
- 5. Стороны четырехугольника, являющиеся соседними отрезками, называются соседними
- 6. 2. Какие стороны четырехугольника являются соседними, противолежащими?1. Какие вершины четырехугольника являются соседними, противолежащими?
- 7. Обозначьте четырехугольник.Укажите:вершины четырехугольника;стороны четырехугольника;пары соседних вершин;пары противолежащих вершин;пары соседних сторон;пары противолежащих сторон.
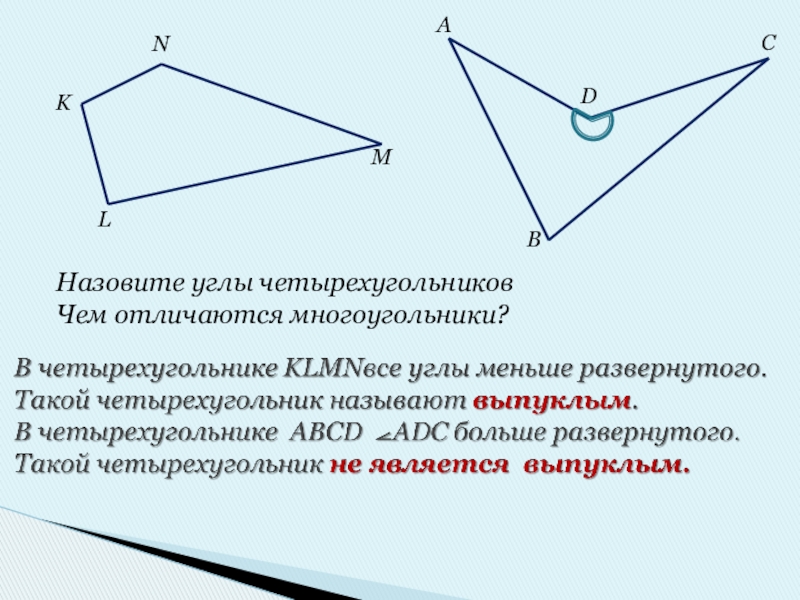
- 8. Назовите углы четырехугольниковЧем отличаются многоугольники?
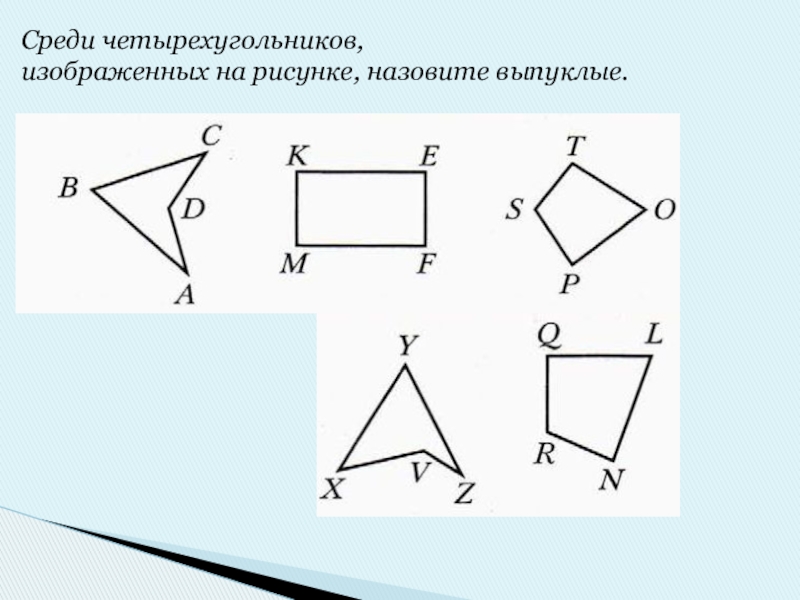
- 9. Среди четырехугольников, изображенных на рисунке, назовите выпуклые.
- 10. Дано:
- 11. 100º90ºЧему равен четвертый угол четырехугольника,
- 12. Длина любой стороны четырехугольника меньше суммы длин
- 13. Может ли у четырехугольника быть:три прямых угла
- 14. Параллелограмм1000Являются ли параллельными прямые:а) BC и ADб)
- 15. ПараллелограммопределениеЧетырехугольник, у которого противолежащие стороны попарно параллельны называется параллелограммом.Биссектриса угла параллелограммаЭлементы параллелограммаСтороны параллелограммаУглы параллелограммаВысота параллелограмма
- 16. АВСDO3. Диагонали точкой пересечения делятся пополамAO=OC
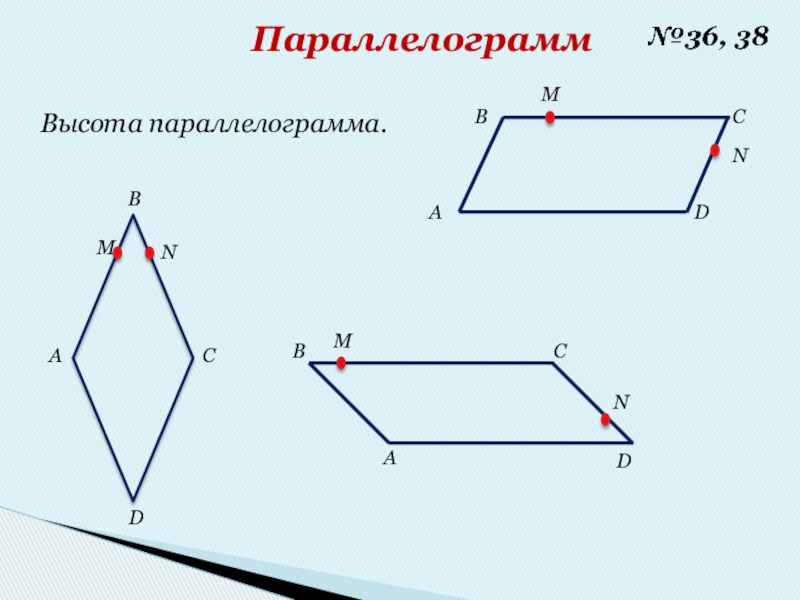
- 17. ПараллелограммВысота параллелограмма.АВСDNM
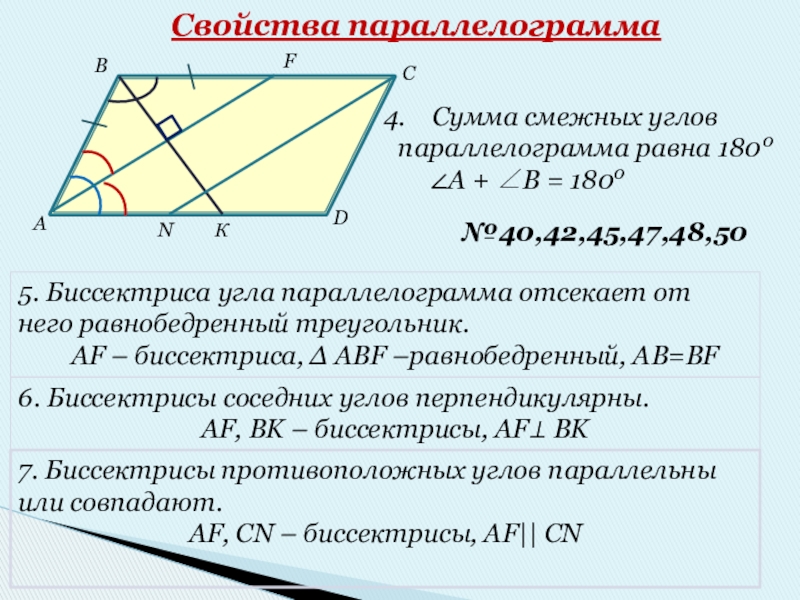
- 18. Свойства параллелограммаСумма смежных углов параллелограмма равна 1800
- 19. Слайд 19
Слайд 2Какая геометрическая фигура называется треугольником?
Элементы треугольника
Виды треугольников, в зависимости от видов
Периметр треугольника
Биссектриса, высота, медиана треугольника
Как называются пары сторон и пары углов в равных треугольниках, которые при наложении совпадают
Треугольник
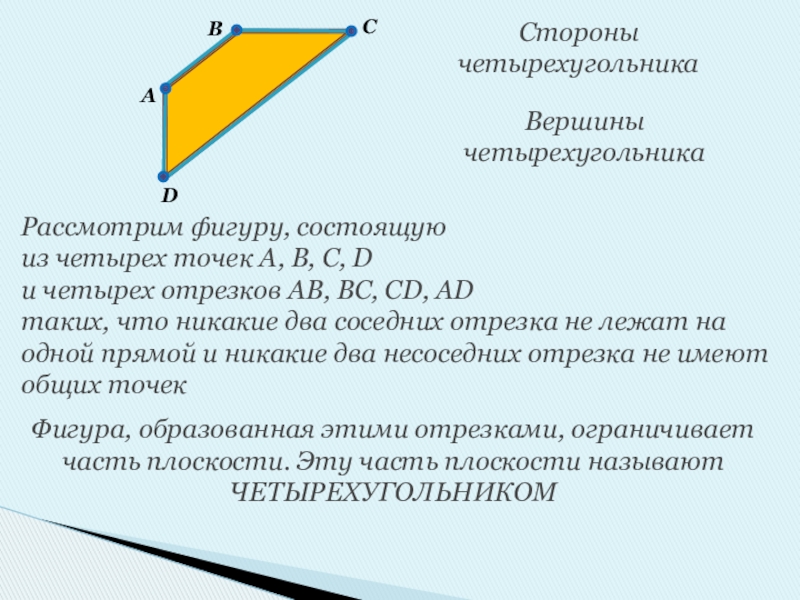
Слайд 3Рассмотрим фигуру, состоящую из четырех точек A, B, C, D и
A
B
C
D
Фигура, образованная этими отрезками, ограничивает часть плоскости. Эту часть плоскости называют ЧЕТЫРЕХУГОЛЬНИКОМ
Вершины четырехугольника
Стороны четырехугольника
Слайд 5Стороны четырехугольника, являющиеся соседними отрезками, называются соседними сторонами четырехугольника
Вершины четырехугольника, являющиеся
Стороны четырехугольника, не являющиеся соседними, называют противолежащими сторонами четырехугольника
Несоседние вершины четырехугольника, называют противолежащими вершинами четырехугольника
Диагональ четырехугольника
A
B
C
D
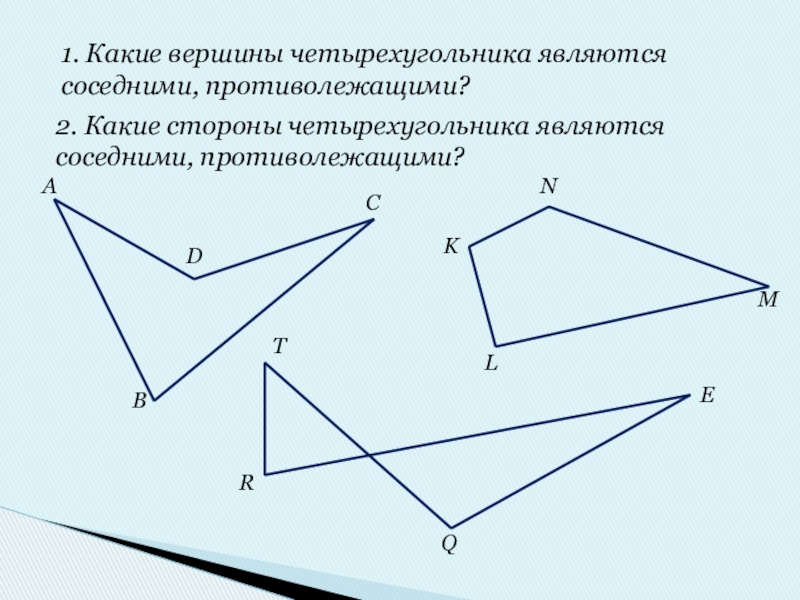
Слайд 62. Какие стороны четырехугольника являются
соседними, противолежащими?
1. Какие вершины четырехугольника являются
соседними, противолежащими?
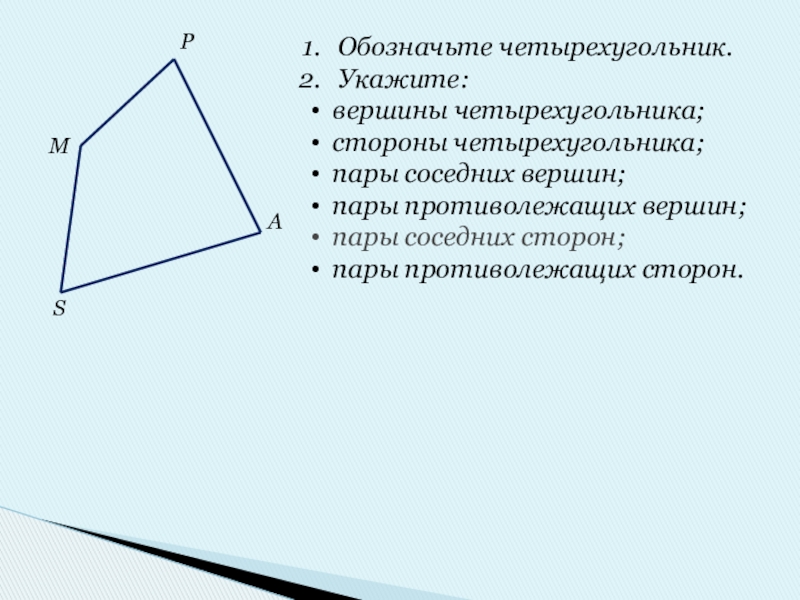
Слайд 7Обозначьте четырехугольник.
Укажите:
вершины четырехугольника;
стороны четырехугольника;
пары соседних вершин;
пары противолежащих вершин;
пары соседних сторон;
пары противолежащих
Слайд 10Дано:
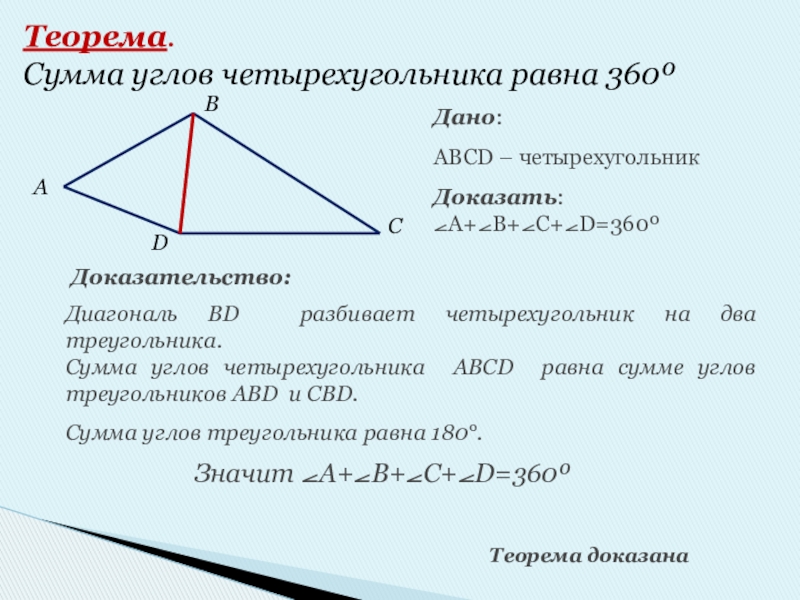
АBCD – четырехугольник
Доказать:
Доказательство:
Диагональ BD разбивает четырехугольник на два треугольника.
Сумма углов треугольника равна 180°.
Сумма углов четырехугольника ABCD равна сумме углов треугольников ABD и CBD.
Значит ⦟А+⦟В+⦟С+⦟D=360º
Теорема доказана
Теорема.
Сумма углов четырехугольника равна 360º
Слайд 11100º
90º
Чему равен четвертый угол четырехугольника, если
Найдите углы четырехугольника, если они равны между собой.
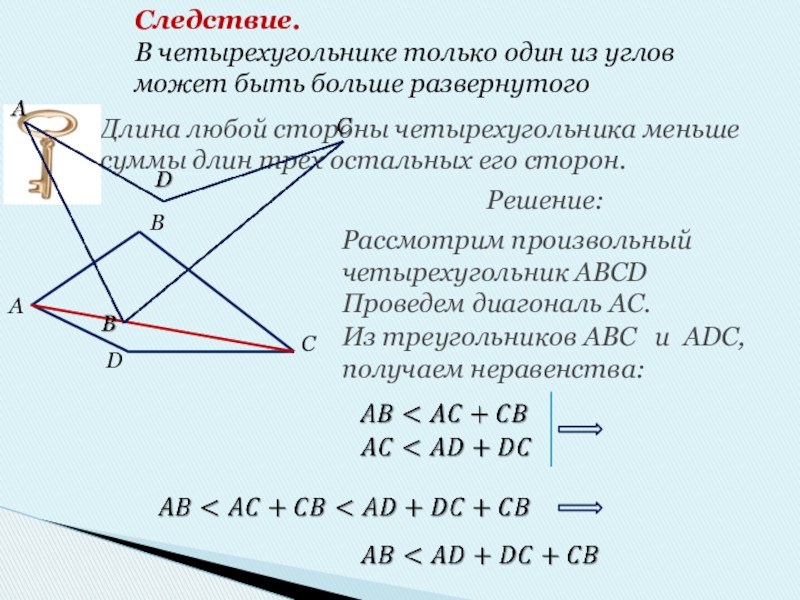
Слайд 12Длина любой стороны четырехугольника меньше суммы длин трех остальных его сторон.
Рассмотрим
Проведем диагональ AC.
Из треугольников ABC и ADC,
получаем неравенства:
Решение:
Следствие.
В четырехугольнике только один из углов
может быть больше развернутого
Слайд 13Может ли у четырехугольника быть:
три прямых угла и один острый;
три прямых
четыре прямых угла;
четыре острых угла;
два прямых и два тупых угла;
два прямых угла, один острый и один тупой?
Могут ли стороны четырехугольника быть
равными:
2 дм, 3 дм, 4 дм, 9 дм;
2 дм, 3 дм, 4 дм, 10 дм?
№11, 16, 22(+), 30, 32, 34
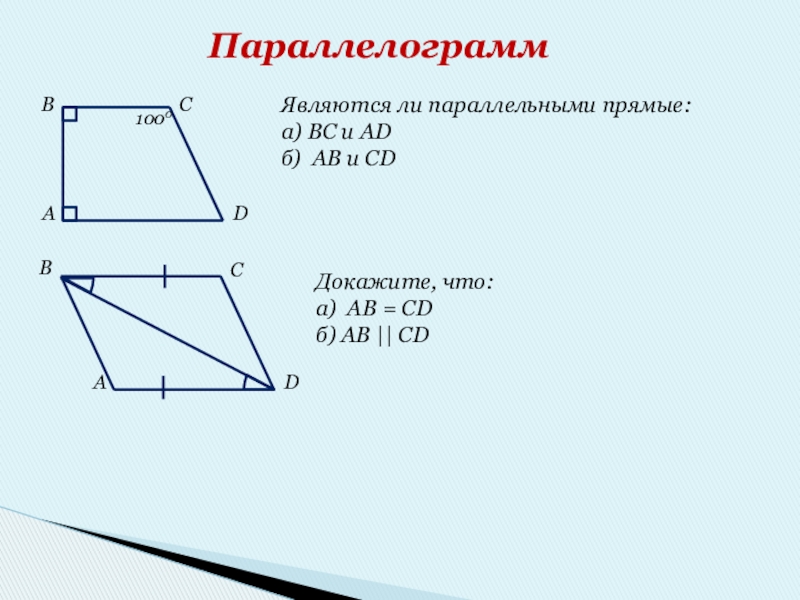
Слайд 14Параллелограмм
1000
Являются ли параллельными прямые:
а) BC и AD
б) AB и CD
Докажите, что:
а)
б) АB || CD
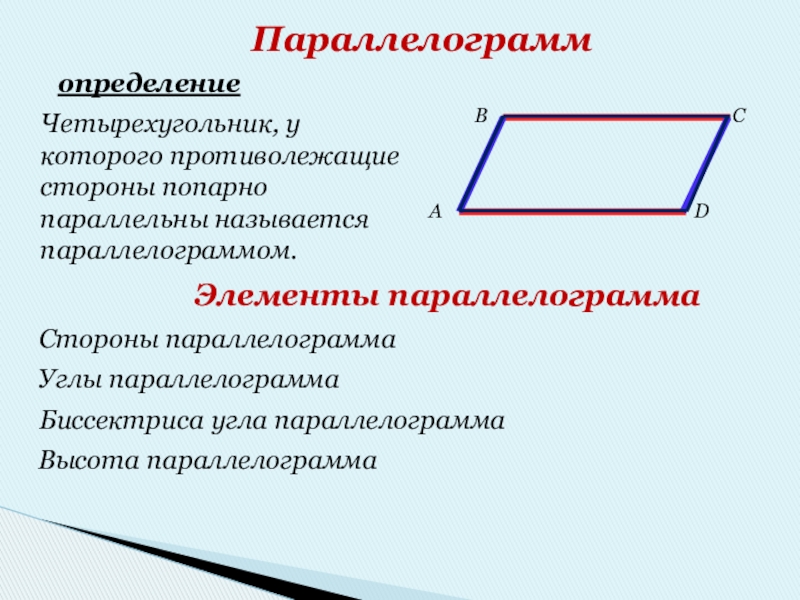
Слайд 15Параллелограмм
определение
Четырехугольник, у которого противолежащие стороны попарно параллельны называется параллелограммом.
Биссектриса угла параллелограмма
Элементы
Стороны параллелограмма
Углы параллелограмма
Высота параллелограмма
Слайд 16А
В
С
D
O
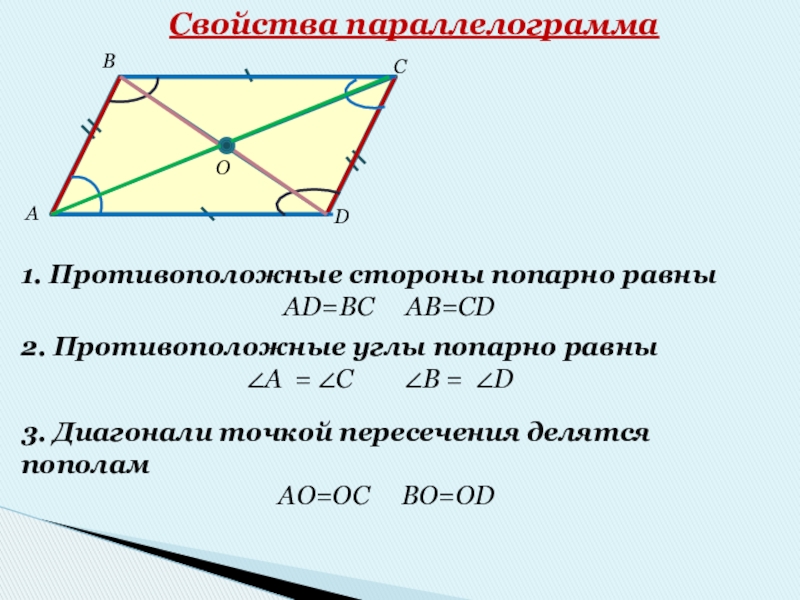
3. Диагонали точкой пересечения делятся пополам
AO=OC BO=OD
Свойства параллелограмма
1.
AD=BC AB=CD
2. Противоположные углы попарно равны
∠А = ∠С ∠В = ∠D
Слайд 18Свойства параллелограмма
Сумма смежных углов
параллелограмма равна 1800
А
В
С
D
5. Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник.
АF – биссектриса, ∆ ABF –равнобедренный, AB=BF
F
6. Биссектрисы соседних углов перпендикулярны.
AF, BK – биссектрисы, AF⊥ BK
К
7. Биссектрисы противоположных углов параллельны или совпадают.
AF, CN – биссектрисы, AF|| CN
N
№40,42,45,47,48,50