- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок в 10-11 классе по геометрии многогранники . Презентация
Содержание
- 1. Урок в 10-11 классе по геометрии многогранники . Презентация
- 2. «Я думаю, что никогда до настоящего времени
- 3. Многоугольником называется плоская фигура, ограниченная
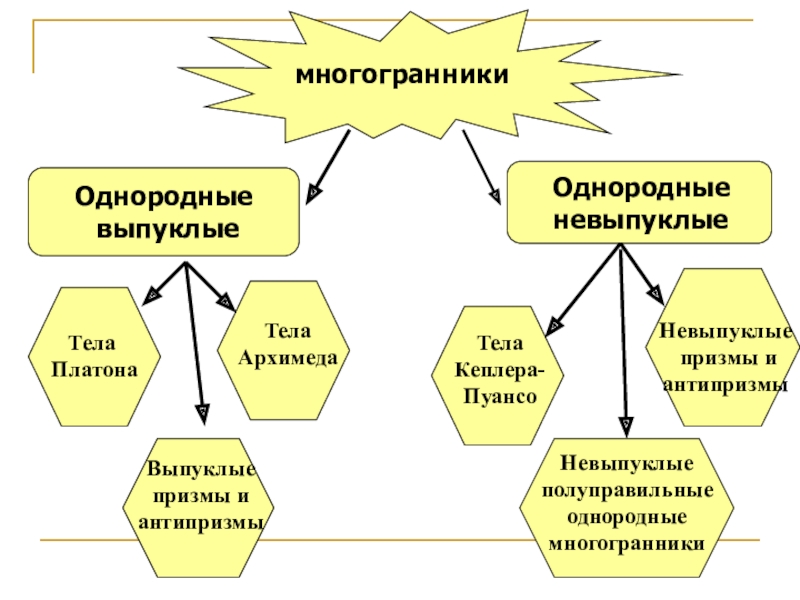
- 4. Однородные выпуклые
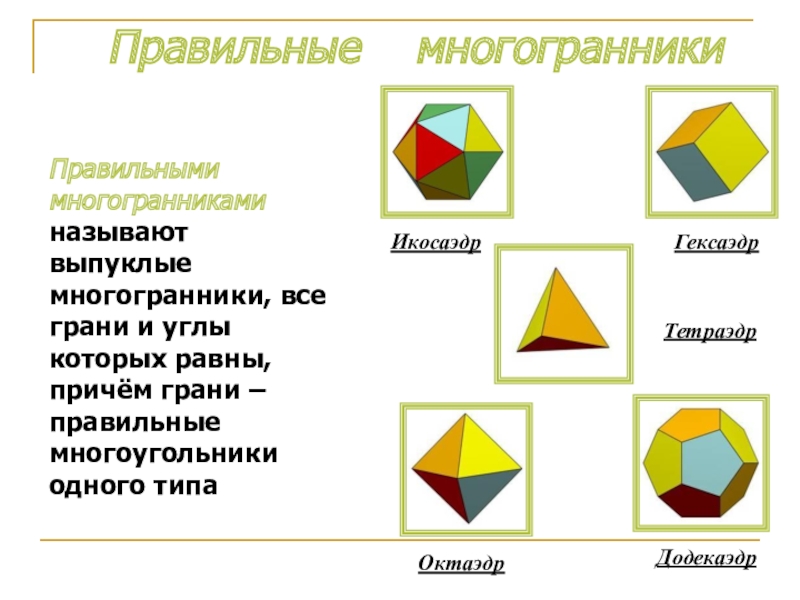
- 5. Правильные многогранники ТетраэдрГексаэдрИкосаэдрОктаэдрДодекаэдрПравильными многогранниками называют
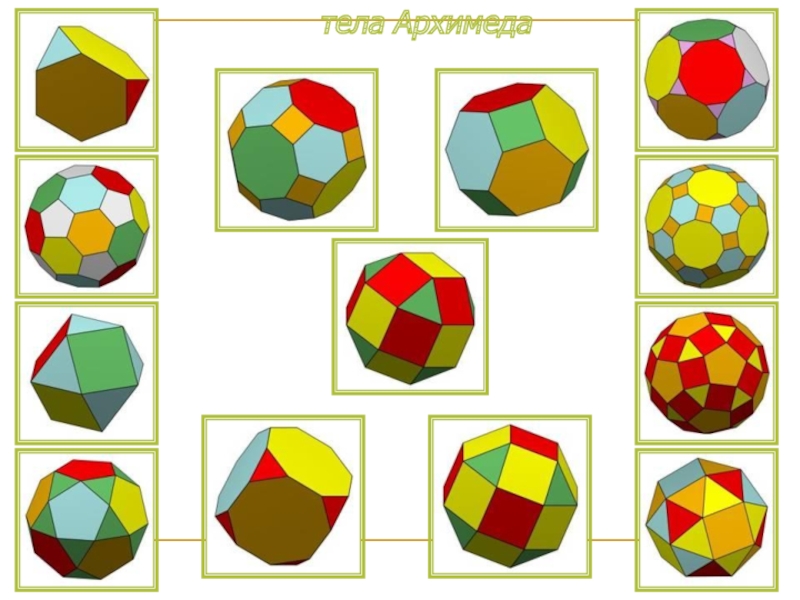
- 6. Архимедовыми телами называют выпуклые многогранники, все многогранные
- 7. тела Архимеда
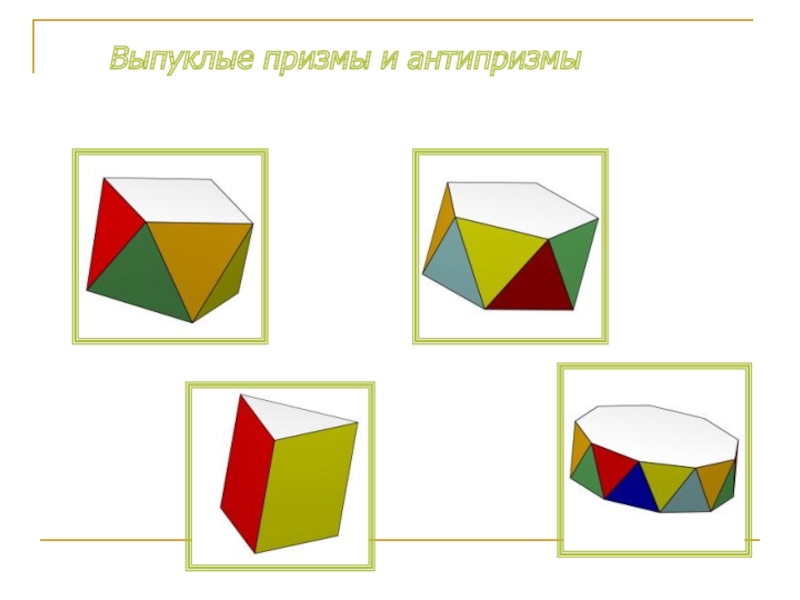
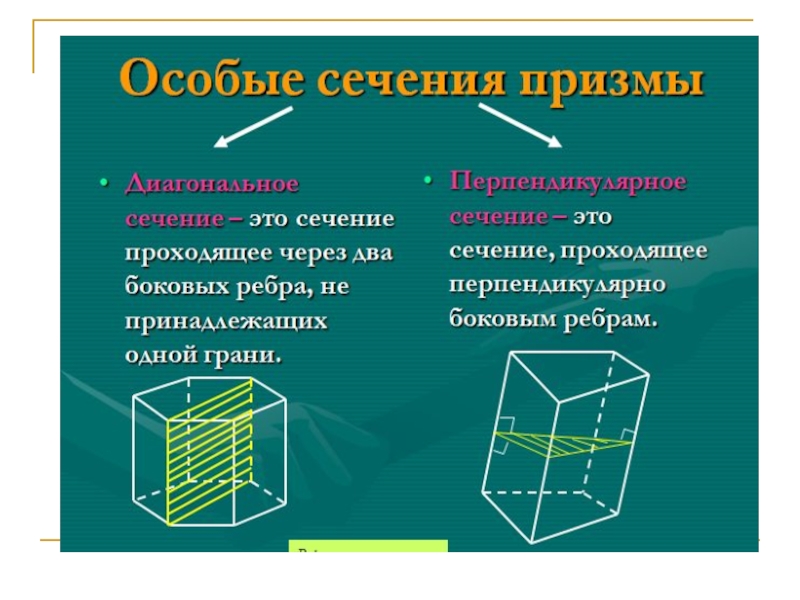
- 8. Выпуклые призмы и антипризмы
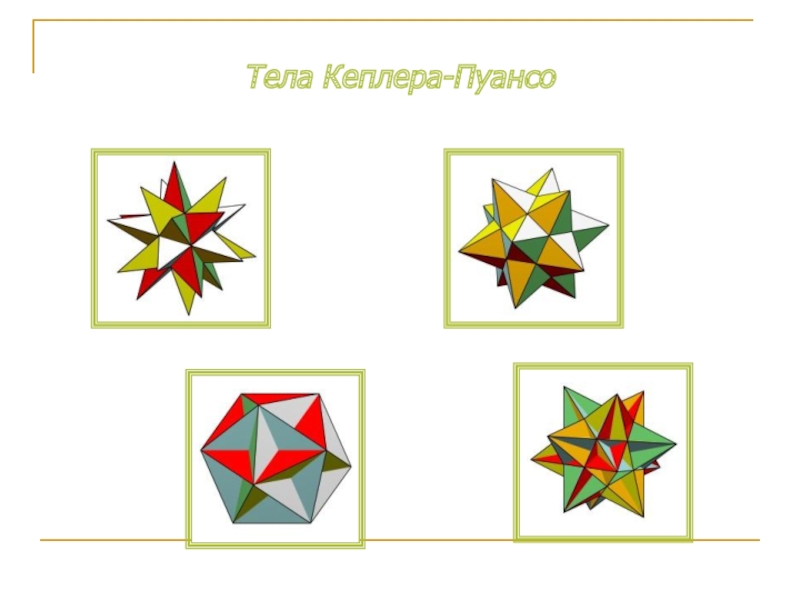
- 9. Тела Кеплера-Пуансо
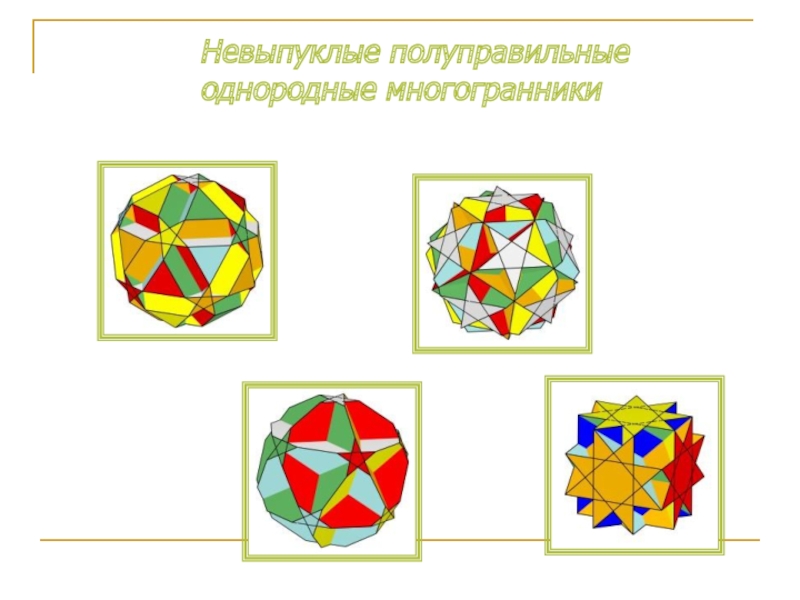
- 10. Невыпуклые полуправильные однородные многогранники
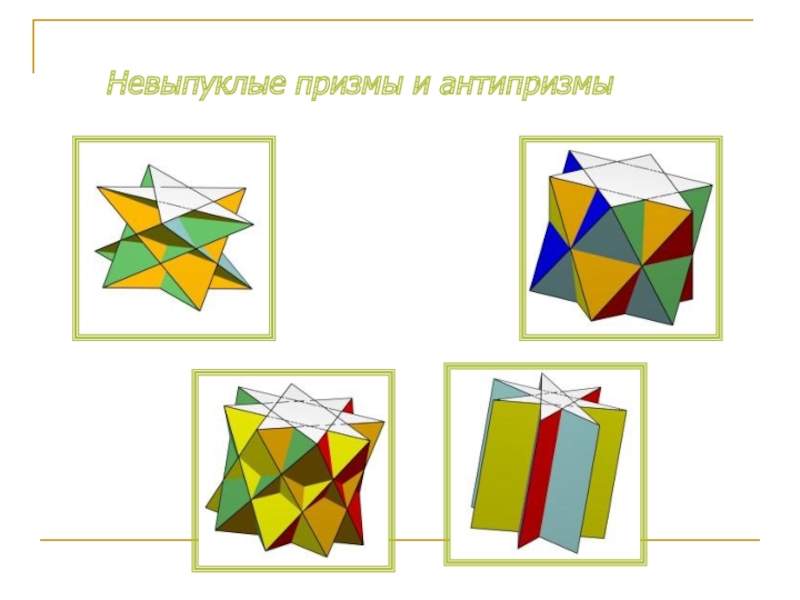
- 11. Невыпуклые призмы и антипризмы
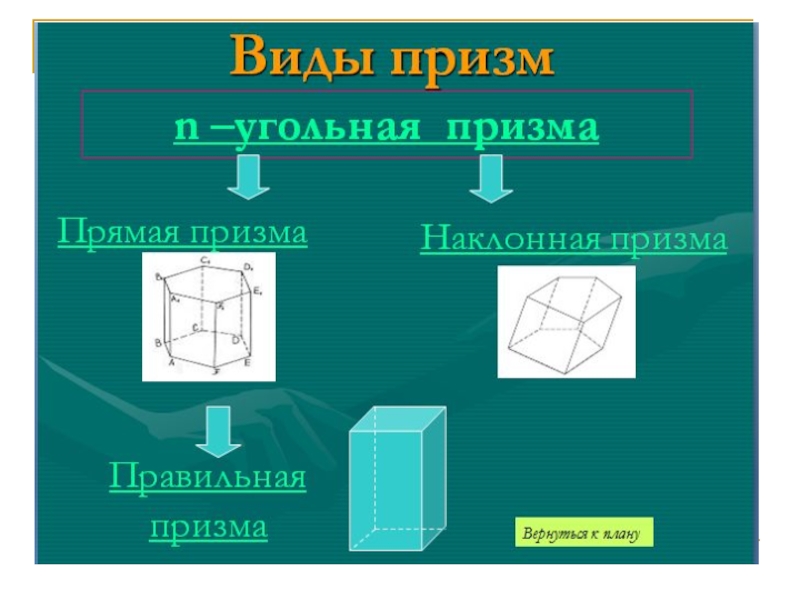
- 12. Призма.
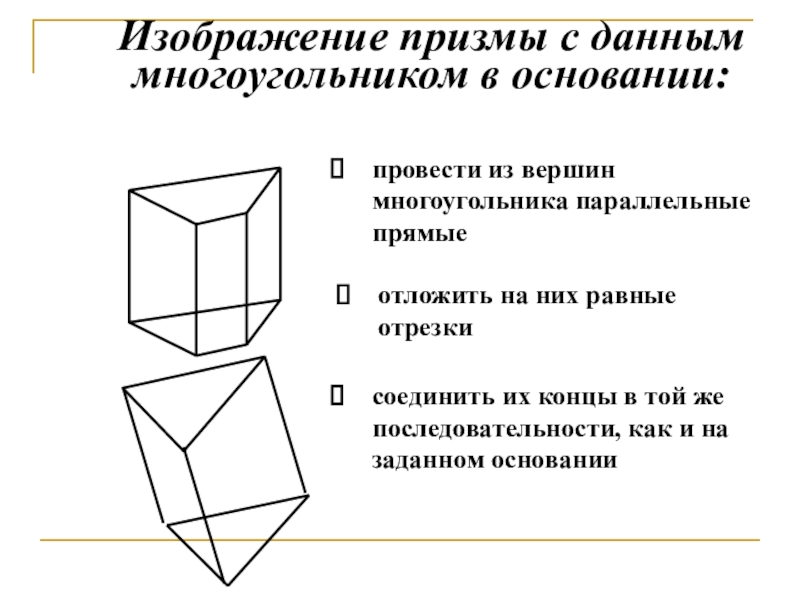
- 13. Изображение призмы с данным многоугольником в основании:
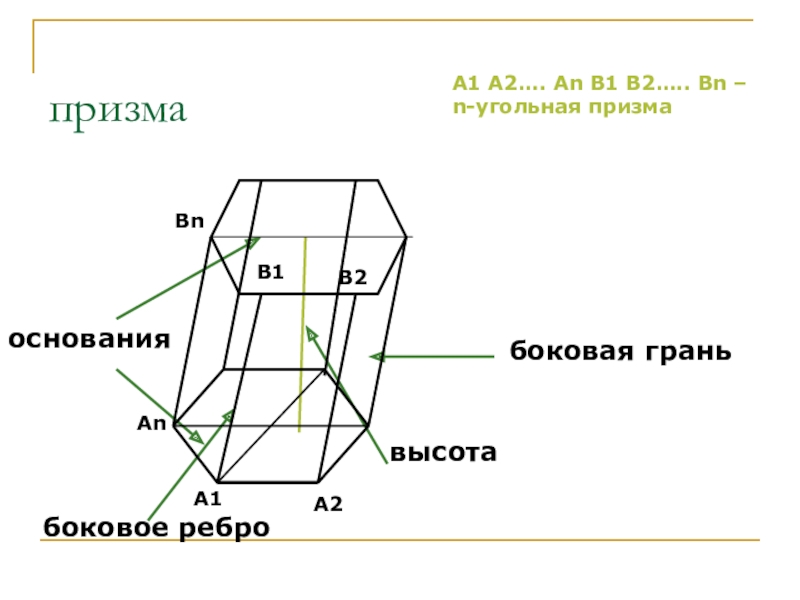
- 14. призмаоснованиябоковая граньвысотабоковое реброA1AnA2В1ВnВ2A1 A2…. An В1 В2….. Вn – n-угольная призма
- 15. Общие свойства призмыОснования призмы равныОснования
- 16. Площадь поверхности призмыПлощадью полной поверхности призмы называется
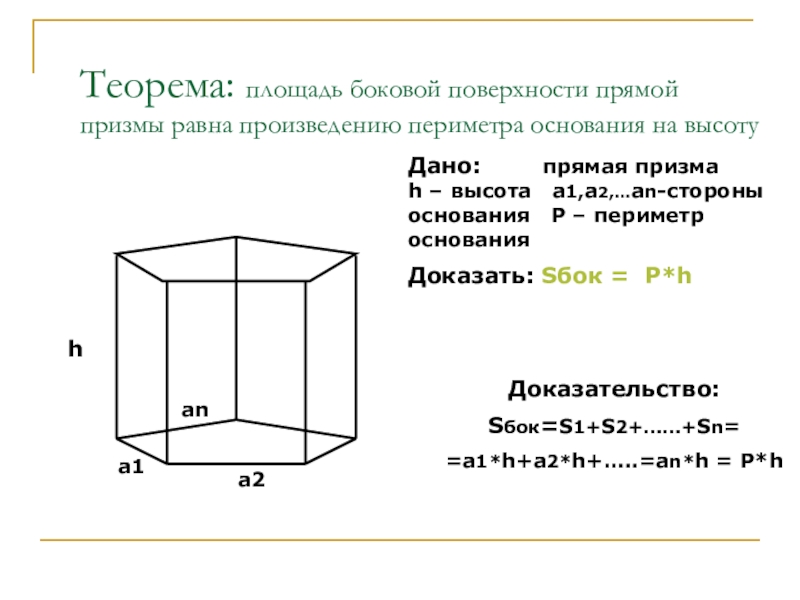
- 17. Теорема: площадь боковой поверхности прямой призмы равна
- 18. Слайд 18
- 19. Слайд 19
- 20. Слайд 20
- 21. Слайд 21
- 22. Слайд 22
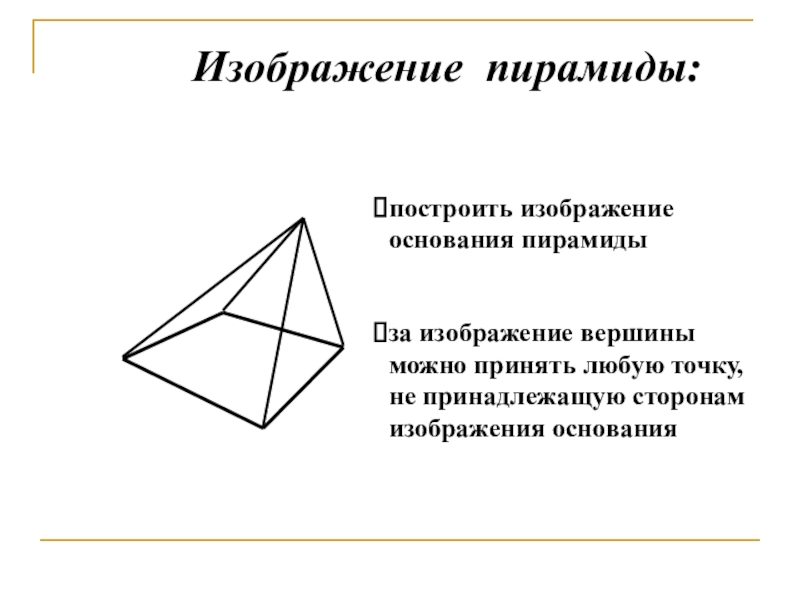
- 23. построить изображение основания пирамидыИзображение пирамиды:за изображение вершины
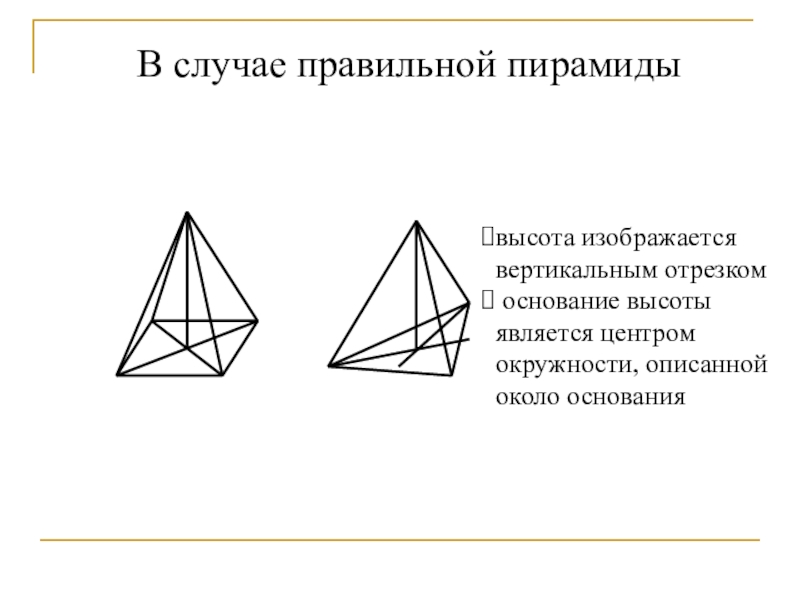
- 24. высота изображается вертикальным отрезком основание высоты является центром окружности, описанной около основания В случае правильной пирамиды
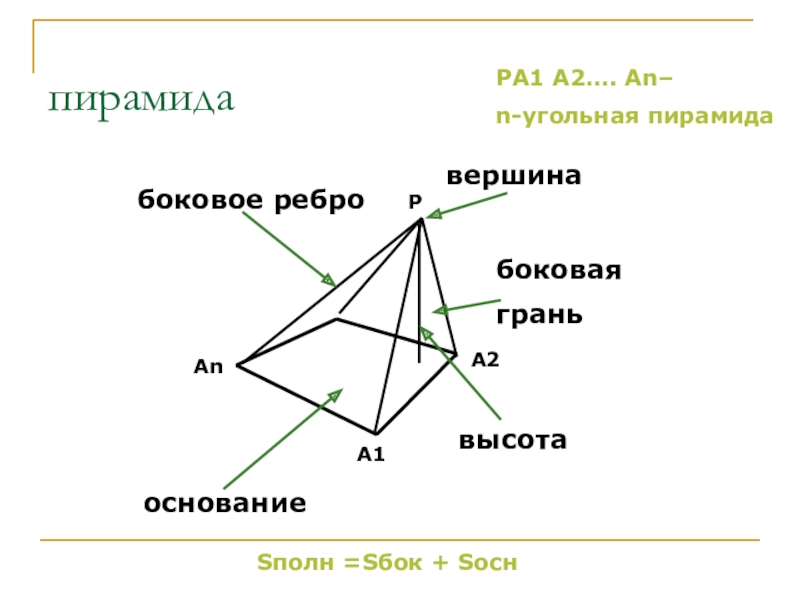
- 25. пирамидаоснованиебоковая граньвысотабоковое ребровершинаSполн =Sбок + SоснA1AnA2PPA1 A2…. An– n-угольная пирамида
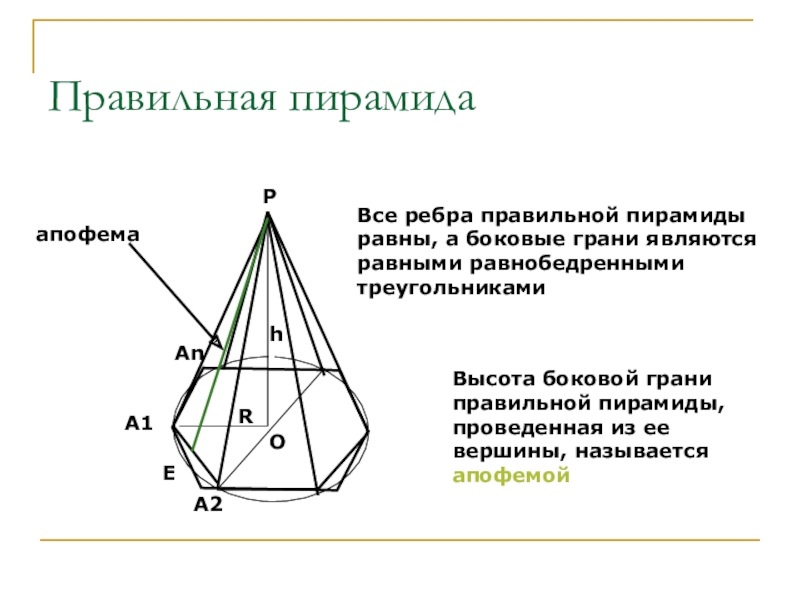
- 26. Правильная пирамидаОPhERA1AnA2Все ребра правильной пирамиды равны, а
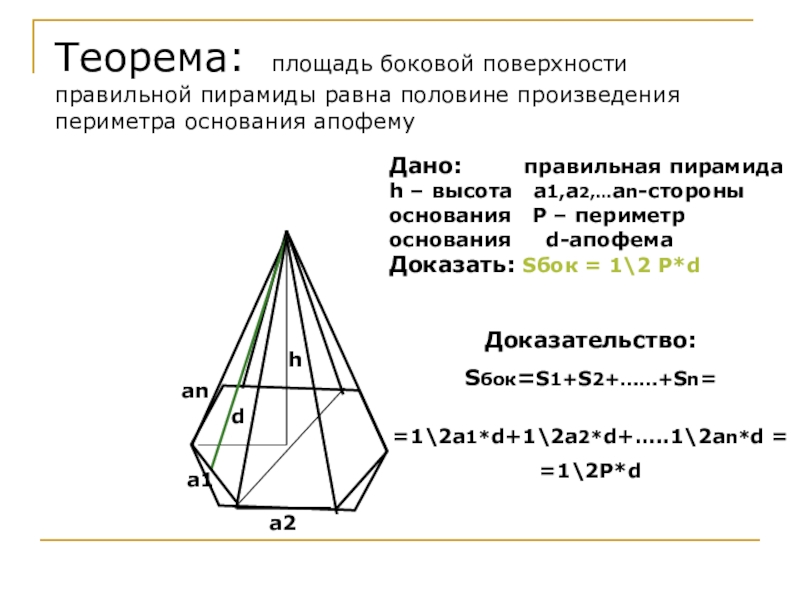
- 27. Теорема: площадь боковой поверхности правильной пирамиды равна
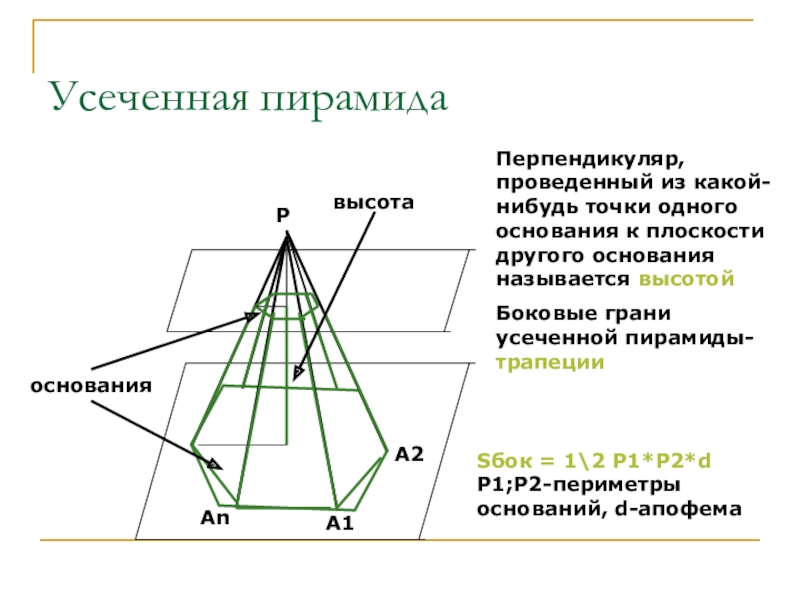
- 28. Усеченная пирамидаПерпендикуляр, проведенный из какой-нибудь точки одного
«Я думаю, что никогда до настоящего времени мы не жили в такой геометрический период. Все вокруг - геометрия»Ле Корбюдзе
Слайд 2«Я думаю, что никогда до настоящего времени мы не жили в
такой геометрический период. Все вокруг - геометрия»
Ле Корбюдзе
Слайд 3 Многоугольником называется плоская фигура, ограниченная отрезками прямых
По
аналогии, многогранник можно определить как часть пространства, ограниченную плоскими многоугольниками
Слайд 5 Правильные многогранники
Тетраэдр
Гексаэдр
Икосаэдр
Октаэдр
Додекаэдр
Правильными многогранниками называют выпуклые многогранники, все грани
и углы которых равны, причём грани – правильные многоугольники одного типа
Слайд 6Архимедовыми телами называют выпуклые многогранники, все многогранные углы которых равны, а
грани – правильные многоугольники нескольких типов
Архимедовы тела
Слайд 13Изображение призмы с данным многоугольником в основании:
соединить их концы в
той же последовательности, как и на заданном основании
провести из вершин многоугольника параллельные прямые
отложить на них равные отрезки
Слайд 14призма
основания
боковая грань
высота
боковое ребро
A1
An
A2
В1
Вn
В2
A1 A2…. An В1 В2….. Вn – n-угольная призма
Слайд 15 Общие свойства призмы
Основания призмы равны
Основания призмы лежат в параллельных
плоскостях
У призмы боковые рёбра параллельны и равны
Любая боковая грань является параллелограммом
У призмы боковые рёбра параллельны и равны
Любая боковая грань является параллелограммом
Слайд 16Площадь поверхности призмы
Площадью полной поверхности призмы называется сумма площадей всех ее
граней, а площадью боковой поверхности призмы – сумма площадей ее боковых граней
Sполн =Sбок + 2Sосн
Sполн =Sбок + 2Sосн
Слайд 17Теорема: площадь боковой поверхности прямой призмы равна произведению периметра основания на
высоту
Дано: прямая призма h – высота а1,а2,…аn-стороны основания P – периметр основания
Доказать: Sбок = P*h
Доказательство:
Sбок=S1+S2+……+Sn=
=а1*h+а2*h+…..=аn*h = P*h
h
а1
а2
аn
Слайд 23построить изображение основания пирамиды
Изображение пирамиды:
за изображение вершины можно принять любую точку,
не принадлежащую сторонам изображения основания
Слайд 24высота изображается
вертикальным отрезком
основание высоты является центром окружности, описанной около
основания
В случае правильной пирамиды
Слайд 25пирамида
основание
боковая
грань
высота
боковое ребро
вершина
Sполн =Sбок + Sосн
A1
An
A2
P
PA1 A2…. An–
n-угольная пирамида
Слайд 26Правильная пирамида
О
P
h
E
R
A1
An
A2
Все ребра правильной пирамиды равны, а боковые грани являются равными
равнобедренными треугольниками
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой
апофема
Слайд 27Теорема: площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания
апофему
h
d
а1
а2
аn
Дано: правильная пирамида h – высота а1,а2,…аn-стороны основания P – периметр основания d-апофема Доказать: Sбок = 1\2 P*d
Доказательство:
Sбок=S1+S2+……+Sn=
=1\2а1*d+1\2а2*d+…..1\2аn*d =
=1\2P*d
Слайд 28Усеченная пирамида
Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого
основания называется высотой
Боковые грани усеченной пирамиды-трапеции
Боковые грани усеченной пирамиды-трапеции
высота
основания
Sбок = 1\2 P1*P2*d P1;P2-периметры оснований, d-апофема
P
A1
An
A2
