Презентация, доклад на тему Урок на тему Теорема Пифагора

Содержание

Теорема Пифагора обнаружена в различных древних задачах и чертежах Папирус времен фараона Аменемхета I (ок. 2000 г. до н.э.)

Слайд 1Теорема Пифагора
История,
доказательства,
применение

Теорема ПифагораИстория, доказательства, применение

Слайд 2Теорема Пифагора обнаружена в различных древних задачах и чертежах
Папирус времен

фараона Аменемхета I
(ок. 2000 г. до н.э.)
Теорема Пифагора обнаружена в различных древних задачах и чертежах Папирус времен фараона Аменемхета I (ок. 2000 г.

Слайд 3 Вавилонские клинописные таблички эпохи царя Хаммурапи (XVIII в. до н.э.)

Вавилонские клинописные таблички эпохи царя Хаммурапи (XVIII в. до н.э.)

Слайд 4 Древнеиндийский геометрическо-теологический
трактат «Сульва сутра»
(«Правила веревки» VI–V вв. до

н.э.)
Древнеиндийский геометрическо-теологический трактат «Сульва сутра» («Правила веревки» VI–V вв. до н.э.)

Слайд 5В древнейшем китайском трактате
«Чжоуби суань цзинь», время создания которого точно

не известно, утверждается, что в XII в. до н.э. китайцы знали свойства египетского треугольника, а к VI в. до н.э.— и общий вид теоремы
В древнейшем китайском трактате «Чжоуби суань цзинь», время создания которого точно не известно, утверждается, что в XII

Слайд 6Пифагор
ок. 570 – 500 гг. до н.э.
Письменных документов о Пифагоре

Самосском не осталось.
А по более поздним свидетельствам трудно восстановить картину его жизни и достижений
Пифагор ок. 570 – 500 гг. до н.э.Письменных документов о Пифагоре Самосском не осталось.А по более поздним

Слайд 7Известно, что Пифагор покинул свой родной остров Самос в Эгейском море

у берегов Малой Азии в знак протеста против тирании правителя
Известно, что Пифагор покинул свой родной остров Самос в Эгейском море у берегов Малой Азии в знак

Слайд 8И уже в зрелом возрасте появился в городе Кротоне на юге

Италии
И уже в зрелом возрасте появился в городе Кротоне на юге Италии

Слайд 9Пифагорейцы узнавали друг друга по звездному пятиугольнику – пентаграмме
Пифагор и его

последователи образовали тайный союз, сыгравший немалую роль в жизни греческих колоний Италии
Пифагорейцы узнавали друг друга по звездному пятиугольнику – пентаграммеПифагор и его последователи образовали тайный союз, сыгравший немалую

Слайд 10

Пифагор.
Фрагмент фрески
«Афинская школа».
Рафаэль. 1511 г.

Слайд 11
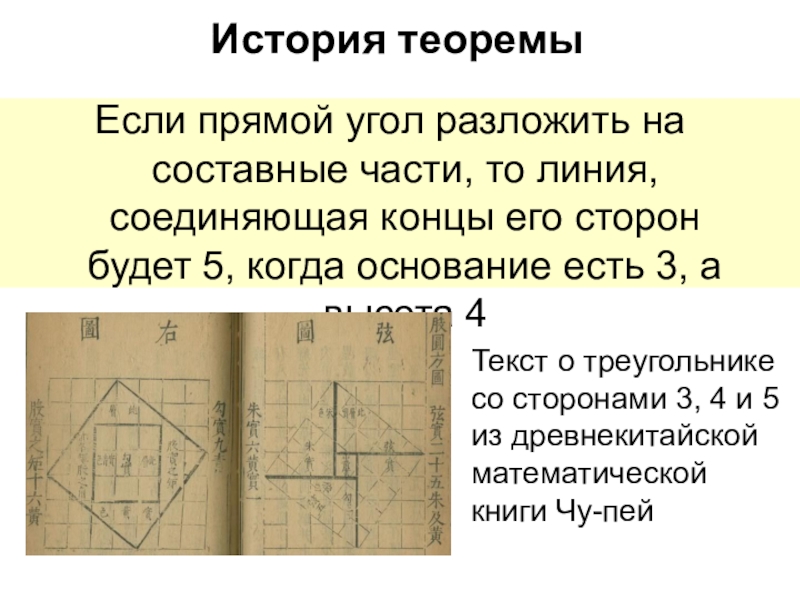
История теоремы
Если прямой угол разложить на составные части, то линия, соединяющая

концы его сторон будет 5, когда основание есть 3, а высота 4


Текст о треугольнике
со сторонами 3, 4 и 5
из древнекитайской математической книги Чу-пей

История теоремыЕсли прямой угол разложить на составные части, то линия, соединяющая концы его сторон будет 5, когда

Слайд 12Весьма вероятно,
что теорема
о квадрате гипотенузы
была известна
в Индии


уже около
XVIII века до н.э.
Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около XVIII века до н.э.

Слайд 13В первом русском переводе с греческого «Начал» Евклида, сделанном
Ф.И. Петрушевским


в 1819 – 1835 гг.,
теорема Пифагора изложена так:

В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол

В первом русском переводе с греческого «Начал» Евклида, сделанном Ф.И. Петрушевским в 1819 – 1835 гг., теорема

Слайд 14Неалгебраические доказательства
Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных

на его катетах

1. С помощью мозаики

Неалгебраические доказательстваКвадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах1. С помощью мозаики

Слайд 152. Древнекитайское доказательство
Математические трактаты Древнего Китая дошли до нас в редакции

II в. до н.э., когда была изобретена бумага. В 213 г. до н.э. китайский император Ши Хуанди, стремясь ликвидировать прежние традиции, приказал сжечь все древние книги
2. Древнекитайское доказательствоМатематические трактаты Древнего Китая дошли до нас в редакции II в. до н.э., когда была

Слайд 163. Древнеиндийское доказательство
«Смотри!»


Чертеж из трактата
«Сиддханта широмани»
(«Венец знания»)
индийского математика


XII в. Бхаскары
3. Древнеиндийское доказательство«Смотри!»Чертеж из трактата «Сиддханта широмани» («Венец знания») индийского математика XII в. Бхаскары

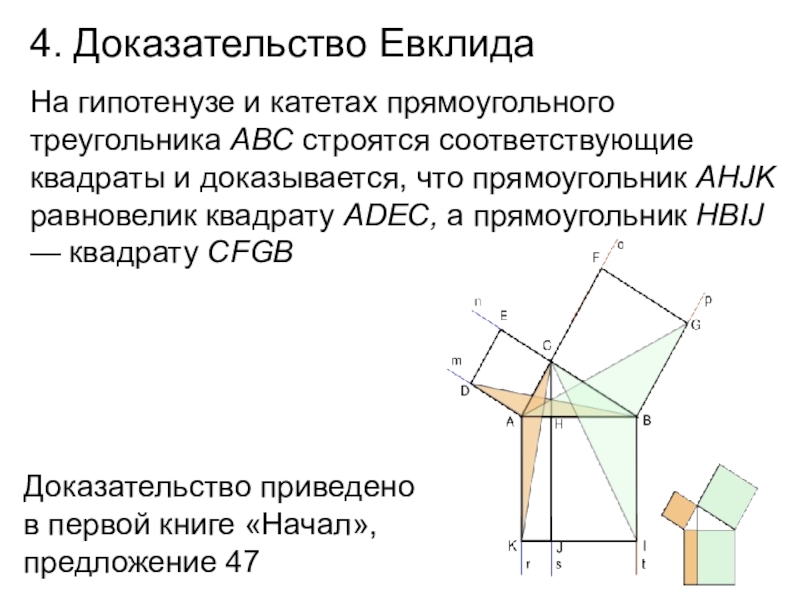
Слайд 174. Доказательство Евклида
Доказательство приведено в первой книге «Начал», предложение 47
На

гипотенузе и катетах прямоугольного треугольника ABC строятся соответствующие квадраты и доказывается, что прямоугольник AHJK равновелик квадрату ADEC, а прямоугольник HBIJ — квадрату СFGB
4. Доказательство ЕвклидаДоказательство приведено в первой книге «Начал», предложение 47 На гипотенузе и катетах прямоугольного треугольника ABC

Слайд 18Алгебраическое доказательство
Пусть ABC — прямоугольный треугольник
с прямым углом С.

Проведем высоту CD.
По определению косинуса угла
cos A = AD : AC = AC : AB.
Отсюда AB · AD = AC · AC.
Аналогично cos B = BD : BC = BC : AB.
Отсюда AB · BD = BC · BC.
Складывая полученные равенства и учитывая, что AD + DB = AB, получим:
AC · AC + BC · BC = AB(AD + DB) = AB · AB.
Алгебраическое доказательство Пусть ABC — прямоугольный треугольник с прямым углом С. Проведем высоту CD. По определению косинуса

Слайд 19Применение
1. Строительство
Окно
В романской архитектуре часто встречается мотив изображенный на

рисунке
Применение 1. СтроительствоОкно В романской архитектуре часто встречается мотив изображенный на рисунке

Слайд 20В зданиях готического и романского стиля верхние части окон расчленяются каменными

ребрами, которые не только играют роль орнамента, но и способствуют прочности окон.
В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль

Слайд 21В доме задумано построить двускатную крышу (форма в сечении). Какой длины

должны быть стропила, если изготовлены балки AC = 8 м и AB = BF?     

Крыша
При строительстве домов и коттеджей часто встает вопрос о длине стропил для крыши, если уже изготовлены балки

В доме задумано построить двускатную крышу (форма в сечении). Какой длины должны быть стропила, если изготовлены балки

Слайд 22Молниеотвод
Молниеотвод защищает предметы, расстояние до которых от его основания не

превышает его удвоенной высоты

Определите оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту

Молниеотвод Молниеотвод защищает предметы, расстояние до которых от его основания не превышает его удвоенной высоты Определите оптимальное

Слайд 232. Мобильная связь
Какую наибольшую высоту должна иметь антенна, чтобы передачу можно

было принимать в радиусе
R = 200 км, если известно, что радиус Земли равен 6380 км?

Вышка (антенна)

2. Мобильная связьКакую наибольшую высоту должна иметь антенна, чтобы передачу можно было принимать в радиусеR = 200

Слайд 24 Важность теоремы состоит в том, что из нее или с ее

помощью можно вывести большинство теорем геометрии. К сожалению, невозможно привести все доказательства теоремы, однако приведенные примеры убедительно свидетельствуют
об огромном интересе, проявляемом по отношению к ней
Важность теоремы состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии.

Слайд 25Литература
1. Акимова С. Занимательная математика. Спб.: Тригон, 1997.
2. Геометрия 7-9: Учебник

для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.
М.: Просвещение, 2002.
3. Глейзер Г.И. История математики в школе. М.: Просвещение, 1981.
4. Еленьский Ш. По следам Пифагора. М.: Детгиз,1961.
5. Журнал «Математика в школе», № 4, 1991.
6. Литцман В. Теорема Пифагора. М., 1960.
7. Скопец З.А. Геометрические миниатюры. М.: Просвещение,1990.
8. Энциклопедический словарь юного математика. Сост. А.П. Савин. 3-е изд., испр. и доп. М.: Педагогика-Пресс, 1997.
9. Энциклопедия для детей. Математика / Главный редактор М.Д. Аксенова. М.: «Аванта+»,1998.
10. Я познаю мир: Детская энциклопедия: Математика. М., 1997.
Литература1. Акимова С. Занимательная математика. Спб.: Тригон, 1997.2. Геометрия 7-9: Учебник для общеобразовательных учреждений / Л.С. Атанасян,
Скачать презентацию

Похожие презентации

Теорема Чевы на уроке геометрии в 10 классе. Теорема Чевы на уроке геометрии в 10 классе. 200
Проект Оригами и математика Проект Оригами и математика 655
Презентация по математике на тему Симметрия в живой природе (8 класс) Презентация по математике на тему Симметрия в живой природе (8 класс) 270
Презентация по геометрии 8 класс Подготовка к контрольной работе по теме Четырехугольники Презентация по геометрии 8 класс Подготовка к контрольной работе по теме Четырехугольники 399
Урок - смотр знаний по теме Соотношения между сторонами и углами треугольника. 9 класс Урок - смотр знаний по теме Соотношения между сторонами и углами треугольника. 9 класс 220
Презентация по математике на тему Метод координат в пространстве Презентация по математике на тему Метод координат в пространстве 171

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Яндекс.Метрика

Обратная связь

Email: Нажмите что бы посмотреть