Выполнила:
Рыжкова В.А.,
ученица 9 класса
Руководитель:
Букреева Т. А.,
учитель математики
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект Оригами и математика
Содержание
- 1. Проект Оригами и математика
- 2. МОДЕЛЬ ПРОЕКТА Цель: Изучить происхождение оригами и связь
- 3. Гипотеза: Искусство оригами тесно связано с математикой.Актуальность:
- 4. методы исследования:поиск информации из разных источников (специальная литература, интернет ресурсы);наблюдение;практическая работа;анкетирование;анализ и обобщение информации по теме.
- 5. Оригами-это японское искусство складывания бумаги, образовано от японского («oru»-складывать, «kami»-бумага)
- 6. Коробочки «санбо»
- 7. Журавлики хиросимы
- 8. Модульное оригами
- 9. Простое оригами
- 10. Складывание по развёртке
- 11. Мокрое складывание
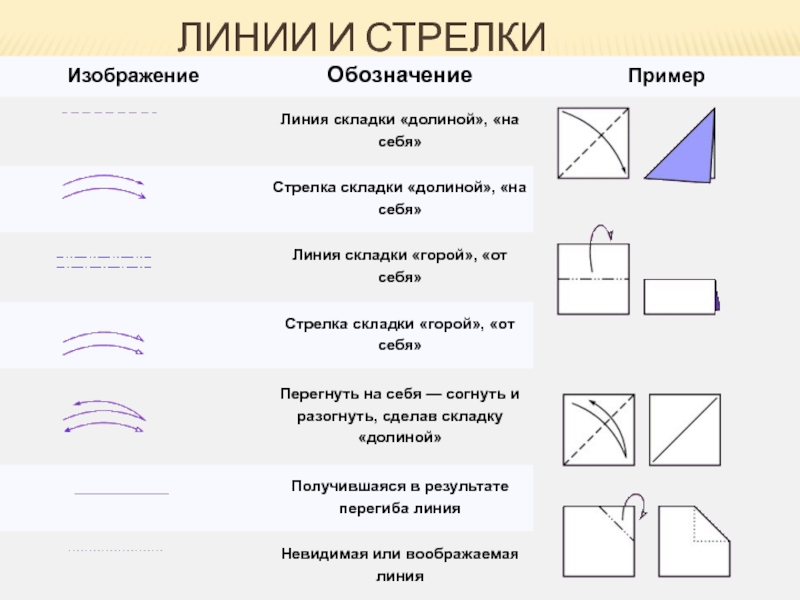
- 12. Линии и стрелки
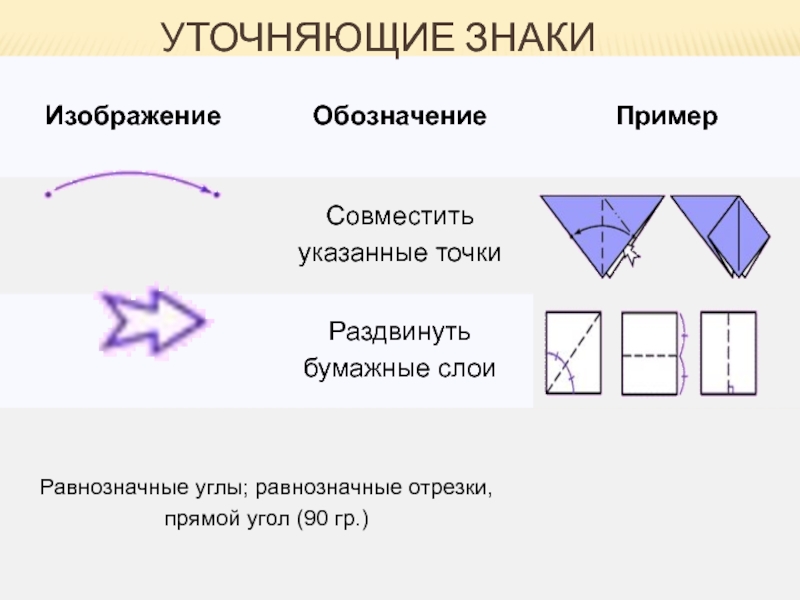
- 13. Уточняющие знаки
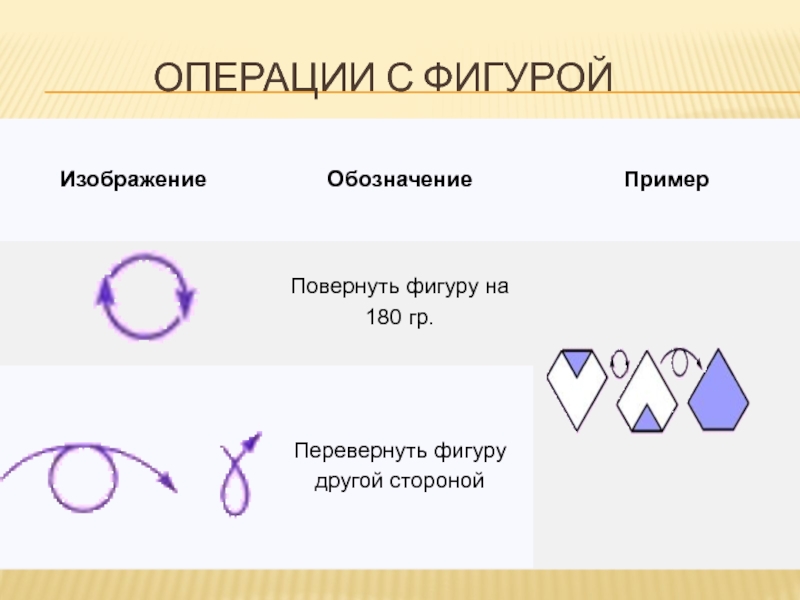
- 14. Операции с фигурой
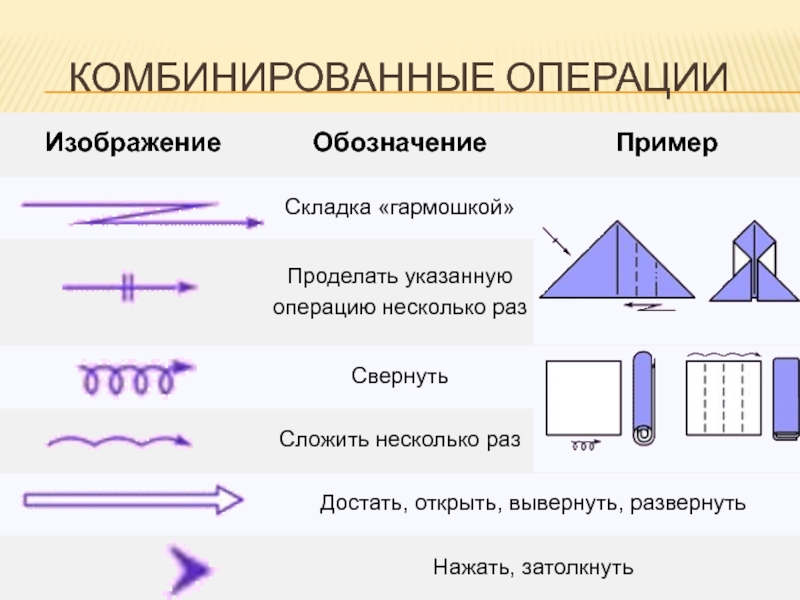
- 15. Комбинированные операции
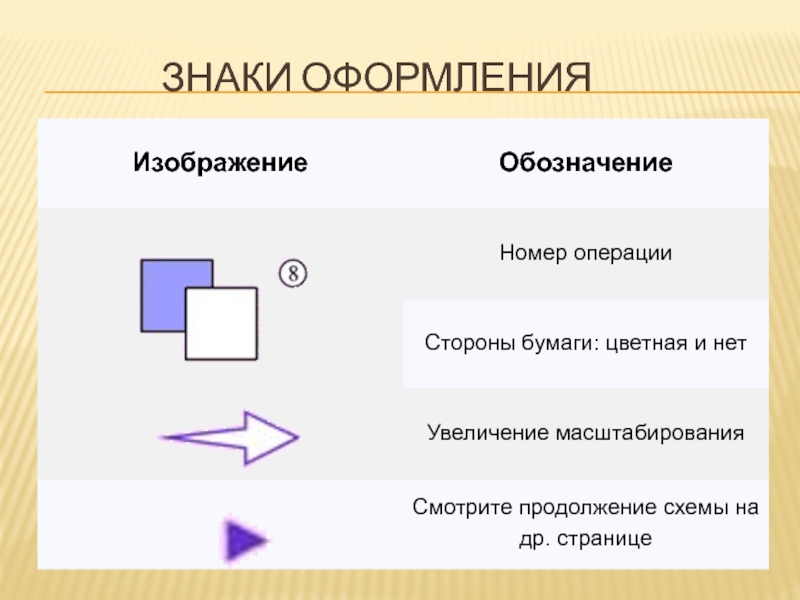
- 16. Знаки оформления
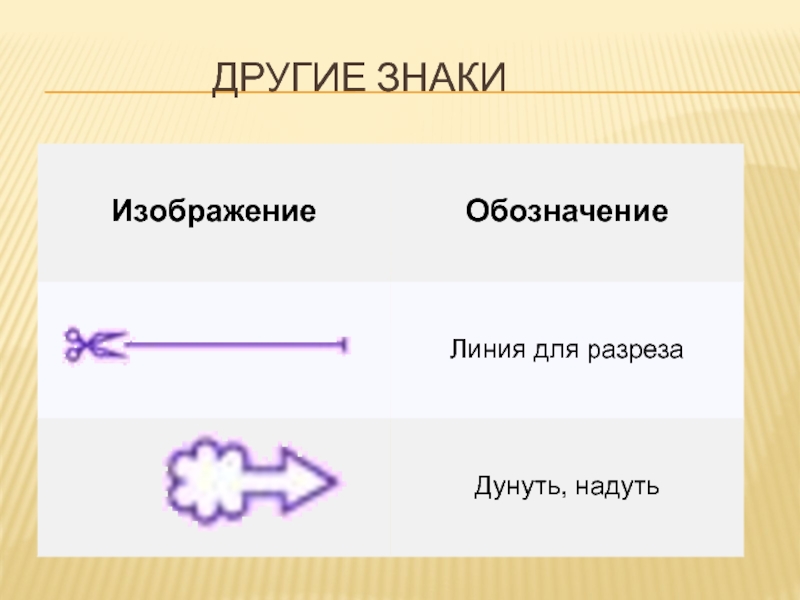
- 17. Другие знаки
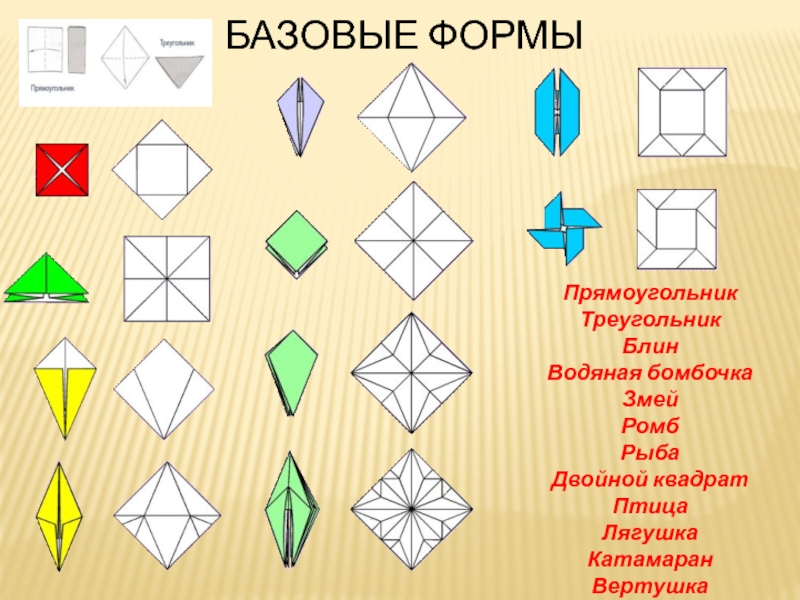
- 18. Базовые формыПрямоугольникТреугольникБлинВодяная бомбочкаЗмейРомбРыбаДвойной квадратПтицаЛягушкаКатамаранВертушка
- 19. Акира йошизава
- 20. Оригаметрия
- 21. Теоремы геометрии и оригами
- 22. Теорема 2. Накрест лежащие углы, образованные при пересечении
- 23. Свойство прямоугольного треугольника: Катет прямоугольного треугольника, лежащий
- 24. Геометрические задачи и оригамиЗадача 1: В ΔАВС проведена
- 25. Задача 2 (на построение): Разделить прямой угол
- 26. Правило 1: Пусть заданы две точки p1 и p2, тогда
- 27. В 2002 году японский оригамист Коширо Хатори
- 28. Оригами в жизни человека
- 29. Коробочки для упаковки
- 30. Цветы
- 31. Салфетки
- 32. Елочные игрушки
- 33. архитектура
- 34. светильник
- 35. мебель
- 36. Слайд 36
- 37. Мои работы
- 38. мухоморчик
- 39. Радужный лебедь
- 40. птенчик
- 41. лесовичок
- 42. кошечка
- 43. Мой мастер класс
- 44. Слайд 44
- 45. Слайд 45
- 46. Вопросы анкетыИзготавливал(а) ли из целого листа бумаги
- 47. Результаты анкетированияФигурки из бумаги изготавливали 32 учащихся,
- 48. выводВ процессе создания проекта мы узнали историю
- 49. Список литературы1.« Забавные фигурки. Модульное оригами». Проснякова
МОДЕЛЬ ПРОЕКТА Цель: Изучить происхождение оригами и связь этого искусства с математикой. Задачи:1. Изучить понятие, виды, историю происхождения оригами.2. Проанализировать связь оригами и математики на примере основных элементов азбуки оригами, решения математических задач.3. Найти способы применения оригами в
Слайд 1МКОУ « Знаменская средняя общеобразовательная школа»
Щигровского района Курской области
Проект
Оригами и математика
Слайд 2МОДЕЛЬ ПРОЕКТА
Цель: Изучить происхождение оригами и связь этого искусства с математикой.
Задачи:
1.
Изучить понятие, виды, историю происхождения оригами.
2. Проанализировать связь оригами и математики на примере основных элементов азбуки оригами, решения математических задач.
3. Найти способы применения оригами в повседневной жизни.
2. Проанализировать связь оригами и математики на примере основных элементов азбуки оригами, решения математических задач.
3. Найти способы применения оригами в повседневной жизни.
Слайд 3Гипотеза: Искусство оригами тесно связано с математикой.
Актуальность: В последнее время ребята
всё с большей неохотой относятся к учёбе, и в частности к математике. Чтобы привлечь внимание учащихся к математике мы решили в своём проекте показать, что математика – это творческая наука.
Слайд 4методы исследования:
поиск информации из разных источников (специальная литература, интернет ресурсы);
наблюдение;
практическая работа;
анкетирование;
анализ
и обобщение информации по теме.
Слайд 5Оригами-это японское искусство складывания бумаги, образовано от японского
(«oru»-складывать, «kami»-бумага)
Слайд 18Базовые формы
Прямоугольник
Треугольник
Блин
Водяная бомбочка
Змей
Ромб
Рыба
Двойной квадрат
Птица
Лягушка
Катамаран
Вертушка
Слайд 20
Оригаметрия – область геометрии,в которой
задачи решаются только методом складывания.
Оригаметрия - область очень молодая, и пока не существует ни соответствующих программ, ни учебников, которые давали бы подобный материал систематически. Вместе с тем многие понятия курса геометрии в школе гораздо проще и нагляднее объясняются с помощью оригаметрии.
Оригаметрия - область очень молодая, и пока не существует ни соответствующих программ, ни учебников, которые давали бы подобный материал систематически. Вместе с тем многие понятия курса геометрии в школе гораздо проще и нагляднее объясняются с помощью оригаметрии.
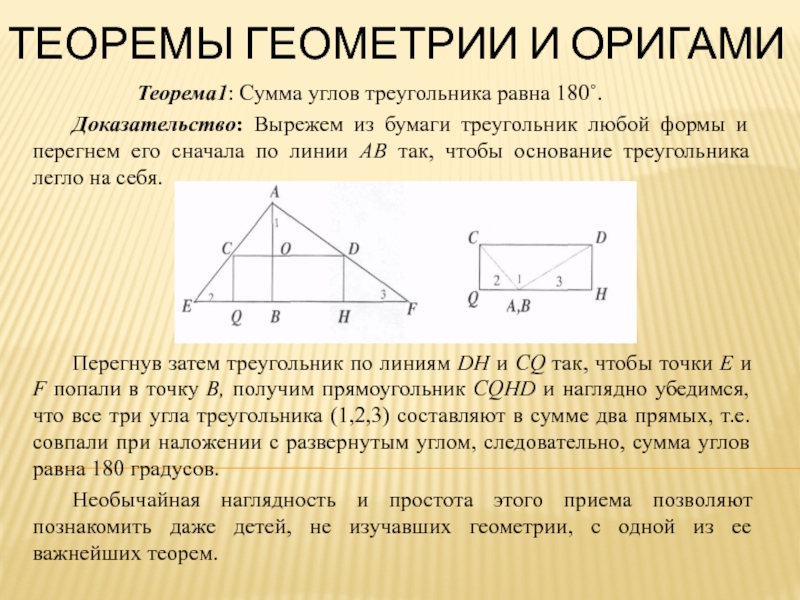
Слайд 21Теоремы геометрии и оригами
Теорема1:
Сумма углов треугольника равна 180˚.
Доказательство: Вырежем из бумаги треугольник любой формы и перегнем его сначала по линии АВ так, чтобы основание треугольника легло на себя.
Перегнув затем треугольник по линиям DH и CQ так, чтобы точки Е и F попали в точку В, получим прямоугольник CQHD и наглядно убедимся, что все три угла треугольника (1,2,3) составляют в сумме два прямых, т.е. совпали при наложении с развернутым углом, следовательно, сумма углов равна 180 градусов.
Необычайная наглядность и простота этого приема позволяют познакомить даже детей, не изучавших геометрии, с одной из ее важнейших теорем.
Доказательство: Вырежем из бумаги треугольник любой формы и перегнем его сначала по линии АВ так, чтобы основание треугольника легло на себя.
Перегнув затем треугольник по линиям DH и CQ так, чтобы точки Е и F попали в точку В, получим прямоугольник CQHD и наглядно убедимся, что все три угла треугольника (1,2,3) составляют в сумме два прямых, т.е. совпали при наложении с развернутым углом, следовательно, сумма углов равна 180 градусов.
Необычайная наглядность и простота этого приема позволяют познакомить даже детей, не изучавших геометрии, с одной из ее важнейших теорем.
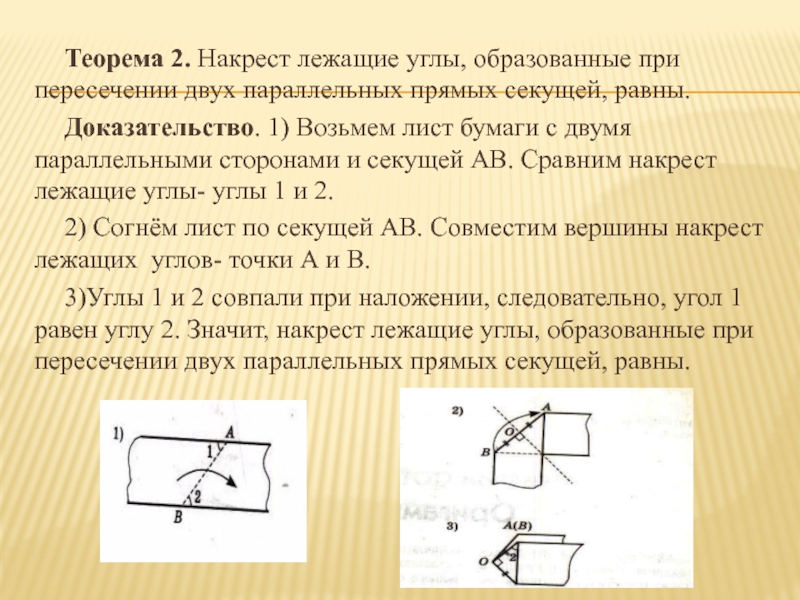
Слайд 22Теорема 2. Накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей,
равны.
Доказательство. 1) Возьмем лист бумаги с двумя параллельными сторонами и секущей АВ. Сравним накрест лежащие углы- углы 1 и 2.
2) Согнём лист по секущей АВ. Совместим вершины накрест лежащих углов- точки А и В.
3)Углы 1 и 2 совпали при наложении, следовательно, угол 1 равен углу 2. Значит, накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей, равны.
Доказательство. 1) Возьмем лист бумаги с двумя параллельными сторонами и секущей АВ. Сравним накрест лежащие углы- углы 1 и 2.
2) Согнём лист по секущей АВ. Совместим вершины накрест лежащих углов- точки А и В.
3)Углы 1 и 2 совпали при наложении, следовательно, угол 1 равен углу 2. Значит, накрест лежащие углы, образованные при пересечении двух параллельных прямых секущей, равны.
Слайд 23Свойство прямоугольного треугольника: Катет прямоугольного треугольника, лежащий против угла в 30o,
равен половине гипотенузы.
Доказательство: Наметим середину стороны квадрата. Точка D должна лечь на намеченную линию. Согнем по указанной линии, а потом отогнем угол в первоначальное положение. Точка А должна лечь на намеченную линию. Согнем по указанной линии, а потом отогнем угол в первоначальное положение ΔADN – прямоугольный, острый угол которого 30o. Совместив точки A и D, получим точку Х, а потом отогнём в первоначальное положение. ΔADX равнобедренный и углы при основании равны 30o.
ےXDN=60o,ےXND=60o, значит ΔXDN равносторонний, т.е. DN = NX = AX = 1/2 AN.
Катет DN лежит против угла 30o и равен 1/2 гипотенузы AN.
Доказательство: Наметим середину стороны квадрата. Точка D должна лечь на намеченную линию. Согнем по указанной линии, а потом отогнем угол в первоначальное положение. Точка А должна лечь на намеченную линию. Согнем по указанной линии, а потом отогнем угол в первоначальное положение ΔADN – прямоугольный, острый угол которого 30o. Совместив точки A и D, получим точку Х, а потом отогнём в первоначальное положение. ΔADX равнобедренный и углы при основании равны 30o.
ےXDN=60o,ےXND=60o, значит ΔXDN равносторонний, т.е. DN = NX = AX = 1/2 AN.
Катет DN лежит против угла 30o и равен 1/2 гипотенузы AN.
Слайд 24Геометрические задачи и оригами
Задача 1: В ΔАВС проведена биссектриса ВК. Через точку
К проведена прямая, пересекающая сторону ВС в точке М так, что ВM = МК. Докажите, что КМ //АВ.
Решение: 1) Оригамское решение:
Совместим лучи ВА и ВС, построим биссектрису ВК. Совместим точки В и К, построим точку М. Согнем по линии МК.
2) Математическое обоснование:
BK – биссектриса ΔАВС, тогда ے1 = ے2, BM = MK (по условию) значит ΔBMK – равнобедренный, следовательно ے 2 = ے 3.
Так как ے 1 = ے 2, ے 2 = ے 3, тоے 1 = ے 3, но ے 1 и ے 3 – накрест лежащие при прямых AB и KM и секущей BK, следовательно AB // KM.
Решение: 1) Оригамское решение:
Совместим лучи ВА и ВС, построим биссектрису ВК. Совместим точки В и К, построим точку М. Согнем по линии МК.
2) Математическое обоснование:
BK – биссектриса ΔАВС, тогда ے1 = ے2, BM = MK (по условию) значит ΔBMK – равнобедренный, следовательно ے 2 = ے 3.
Так как ے 1 = ے 2, ے 2 = ے 3, тоے 1 = ے 3, но ے 1 и ے 3 – накрест лежащие при прямых AB и KM и секущей BK, следовательно AB // KM.
Слайд 25Задача 2 (на построение): Разделить прямой угол на три равные части.
Решение:
1) Оригамское решение: Найдем середину стороны. Совмещаем нижний правый угол с серединным перпендикуляром нижней стороны. Намечаем линию сгиба. На развернутом листе получили три равных угла.
2) Математическое обоснование: Предположим, что нам необходимо вписать в квадрат равносторонний треугольник, причем так, чтобы одна из сторон совпадала со стороной квадрата. Вершина треугольника будет лежать на серединном перпендикуляре, т.к. высота и медиана совпадают. Загнув край на 2-ом этапе, мы получаем равенство сторон и, следовательно, местонахождение вершины, причем линия сгиба будет являться биссектрисой угла треугольника, ч. т. д.
2) Математическое обоснование: Предположим, что нам необходимо вписать в квадрат равносторонний треугольник, причем так, чтобы одна из сторон совпадала со стороной квадрата. Вершина треугольника будет лежать на серединном перпендикуляре, т.к. высота и медиана совпадают. Загнув край на 2-ом этапе, мы получаем равенство сторон и, следовательно, местонахождение вершины, причем линия сгиба будет являться биссектрисой угла треугольника, ч. т. д.
Слайд 26Правило 1: Пусть заданы две точки p1 и p2, тогда лист можно сложить так,
что данные две точки будут лежать на складке.
Правило 2: Пусть заданы две точки p1 и p2, тогда лист можно сложить так, что одна точка перейдёт в другую.
Правило 3: Пусть заданы две прямые l1 и l2, тогда лист можно сложить так, что одна прямая перейдёт в другую.
Правило 4: Пусть заданы прямая l1 и точка p1, тогда лист можно сложить так, что точка попадёт на складку, а прямая перейдёт сама в себя (то есть линия складки будет ей перпендикулярна).
Правило 5: Пусть заданы прямая l1 и две точки p1 и p2, тогда лист можно сложить так, что точка p2 попадёт на складку, а p1 — на прямую l1.
Правило 6: Пусть заданы две прямые l1 и l2 и две точки p1 и p2, тогда лист можно сложить так, что точка p1 попадёт на прямую l1, а точка p2 попадёт на прямуюl2.
Правило 2: Пусть заданы две точки p1 и p2, тогда лист можно сложить так, что одна точка перейдёт в другую.
Правило 3: Пусть заданы две прямые l1 и l2, тогда лист можно сложить так, что одна прямая перейдёт в другую.
Правило 4: Пусть заданы прямая l1 и точка p1, тогда лист можно сложить так, что точка попадёт на складку, а прямая перейдёт сама в себя (то есть линия складки будет ей перпендикулярна).
Правило 5: Пусть заданы прямая l1 и две точки p1 и p2, тогда лист можно сложить так, что точка p2 попадёт на складку, а p1 — на прямую l1.
Правило 6: Пусть заданы две прямые l1 и l2 и две точки p1 и p2, тогда лист можно сложить так, что точка p1 попадёт на прямую l1, а точка p2 попадёт на прямуюl2.
Слайд 27В 2002 году японский оригамист Коширо Хатори обнаружил сгиб, который не
описан в правилах Х. Худзита.
Правило 7: Пусть заданы две прямые l1 и l2 и точка p, тогда лист можно сложить так, что точка p попадёт на прямую l1, а прямая l2 перейдёт сама в себя (то есть линия складки будет ей перпендикулярна).
Правило 7: Пусть заданы две прямые l1 и l2 и точка p, тогда лист можно сложить так, что точка p попадёт на прямую l1, а прямая l2 перейдёт сама в себя (то есть линия складки будет ей перпендикулярна).
Слайд 46Вопросы анкеты
Изготавливал(а) ли из целого листа бумаги фигурки?
Где создавал(а) эти фигурки?
Знаешь
ли ты, как называется работа по получению бумажной фигурки путём только перегибания, сгибания листа бумаги?
Как ты изготавливал(а) фигурки: самостоятельно по схеме, вслед за кем-то, по схеме со взрослым?
Какие фигурки ты изготавливал(а)?
Нравится ли тебе изготавливать фигурки из бумаги?
Связано ли занятие складывания фигурок из бумаги с математикой? Почему ты так считаешь?
Желаешь ли ты заниматься изготовлением изделий из бумаги? Что бы ты хотел(а) изготовить?
В анкетировании приняли участие 32 учащихся 5-11 классов
Как ты изготавливал(а) фигурки: самостоятельно по схеме, вслед за кем-то, по схеме со взрослым?
Какие фигурки ты изготавливал(а)?
Нравится ли тебе изготавливать фигурки из бумаги?
Связано ли занятие складывания фигурок из бумаги с математикой? Почему ты так считаешь?
Желаешь ли ты заниматься изготовлением изделий из бумаги? Что бы ты хотел(а) изготовить?
В анкетировании приняли участие 32 учащихся 5-11 классов
Слайд 47Результаты анкетирования
Фигурки из бумаги изготавливали 32 учащихся, нет – 0.
Изготавливали фигурки
в школе, дома, в детском саду – 2 уч., в школе и дома – 15 уч., дома – 29 уч., в школе – 21 уч.
Работа по получению бумажной фигурки называется оригами. Правильный ответ дали 24 учащихся, не знают – 8 учащихся.
Фигурки изготавливали по схеме самостоятельно – 6 учащихся, по схеме со взрослыми -2 учащихся, повторяя за кем-то– 5 учащихся, сначала с помощью, а затем самостоятельно –19 учащихся.
Учащиеся изготавливали самолёт – 29 учащихся, кораблик – 27 учащихся, лягушку – 19 учащихся, цветы – 6 учащихся, хлопушку – 21 учащихся, конверт – 10 учащихся, фонарик-2 учащихся.
Складывать фигурки из бумаги нравится 29 учащимся, не нравится – 3 учащимся.
Занятие оригами связано с математикой считают 32 учащихся, так как при складывании идёт работа с геометрическими фигурами.
Желают изготавливать фигурки из бумаги 22 учащихся. Они хотят научиться изготавливать дома, дворцы, автомобили, мебель.
Работа по получению бумажной фигурки называется оригами. Правильный ответ дали 24 учащихся, не знают – 8 учащихся.
Фигурки изготавливали по схеме самостоятельно – 6 учащихся, по схеме со взрослыми -2 учащихся, повторяя за кем-то– 5 учащихся, сначала с помощью, а затем самостоятельно –19 учащихся.
Учащиеся изготавливали самолёт – 29 учащихся, кораблик – 27 учащихся, лягушку – 19 учащихся, цветы – 6 учащихся, хлопушку – 21 учащихся, конверт – 10 учащихся, фонарик-2 учащихся.
Складывать фигурки из бумаги нравится 29 учащимся, не нравится – 3 учащимся.
Занятие оригами связано с математикой считают 32 учащихся, так как при складывании идёт работа с геометрическими фигурами.
Желают изготавливать фигурки из бумаги 22 учащихся. Они хотят научиться изготавливать дома, дворцы, автомобили, мебель.
Слайд 48вывод
В процессе создания проекта мы узнали историю возникновения оригами, рассмотрели взаимосвязь
оригами с математикой.
Оригами и математика, словно две сестры, которые не терпят неточности и поспешности. Само оригами дает полет фантазии, а математика эту фантазию облачает в платье науки.
По результатам моего исследования можно сделать вывод, что гипотеза подтвердилась – искусство оригами тесно связано с математикой и может стать хорошей основой для ее изучения.
Оригами и математика, словно две сестры, которые не терпят неточности и поспешности. Само оригами дает полет фантазии, а математика эту фантазию облачает в платье науки.
По результатам моего исследования можно сделать вывод, что гипотеза подтвердилась – искусство оригами тесно связано с математикой и может стать хорошей основой для ее изучения.
Слайд 49Список литературы
1.« Забавные фигурки. Модульное оригами». Проснякова Т.Н.-М.:АСТ- ПРЕСС. КНИГА. 2011г.(Золотая
библиотека увлечений).
2. «Оригами. Орнаменты, кусудамы, многогранники». Весновская О.В. Чебоксары, 2003 г.
3.«Правильные многоугольники в оригами». Белим С.Н, Белим С.В. Омск. 2003 г.
4. «Задачи по геометрии, решаемые методами оригами». Белим С.Н. М.: изд. «Аким». 1998г.
5. «Энциклопедия оригами для детей и взрослых». С. Ю. Афонькин, Е.Ю.Афонькина.-С-Пб. «Кристалл» ,2000г.
6. «Оригами. Волшебный квадрат». С. Ю. Афонькин, Е.Ю.Афонькина. Москва, «Аким».2002г.
2. «Оригами. Орнаменты, кусудамы, многогранники». Весновская О.В. Чебоксары, 2003 г.
3.«Правильные многоугольники в оригами». Белим С.Н, Белим С.В. Омск. 2003 г.
4. «Задачи по геометрии, решаемые методами оригами». Белим С.Н. М.: изд. «Аким». 1998г.
5. «Энциклопедия оригами для детей и взрослых». С. Ю. Афонькин, Е.Ю.Афонькина.-С-Пб. «Кристалл» ,2000г.
6. «Оригами. Волшебный квадрат». С. Ю. Афонькин, Е.Ю.Афонькина. Москва, «Аким».2002г.