ShareSlide^ru

Презентация, доклад по математике на тему Многогранники

Содержание

1. Презентация по математике на тему Многогранники
2. Поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, называется многогранником.Понятие многогранника
3. Выпуклые и невыпуклые многогранники
4. Призма
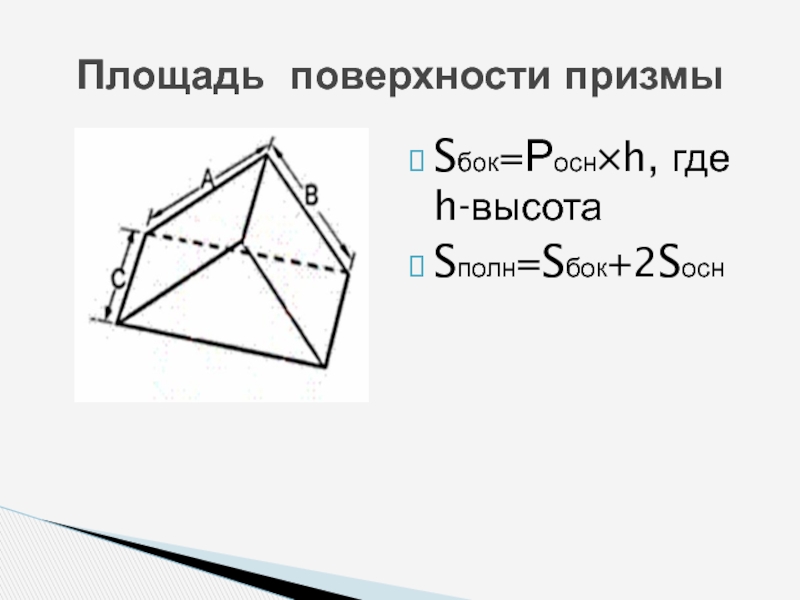
5. Sбок=Росн×h, где h-высотаSполн=Sбок+2SоснПлощадь поверхности призмы
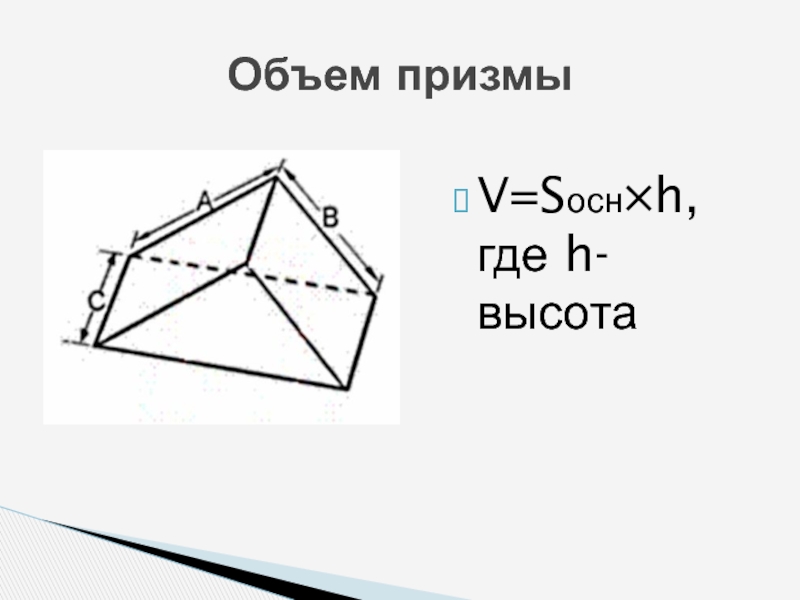
6. V=Sосн×h, где h-высотаОбъем призмы
7. Пирамида
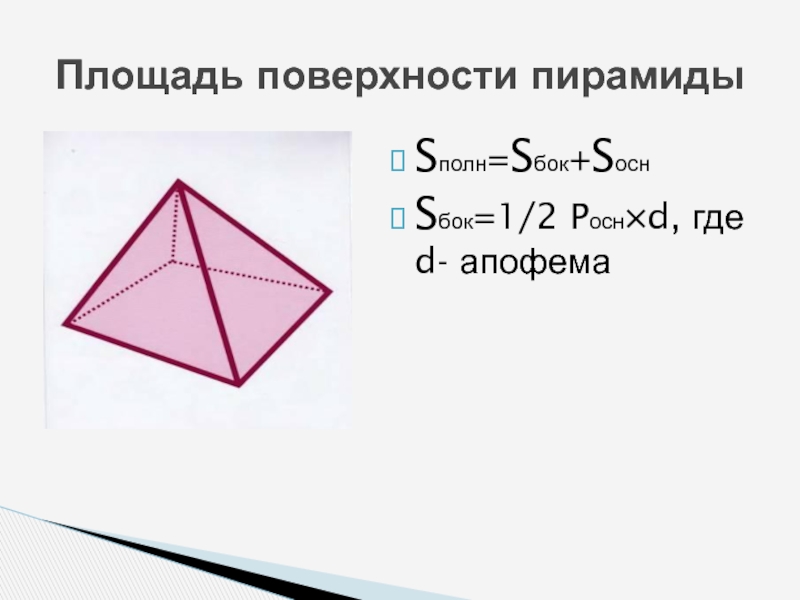
8. Sполн=Sбок+SоснSбок=1/2 Pосн×d, где d- апофемаПлощадь поверхности пирамиды
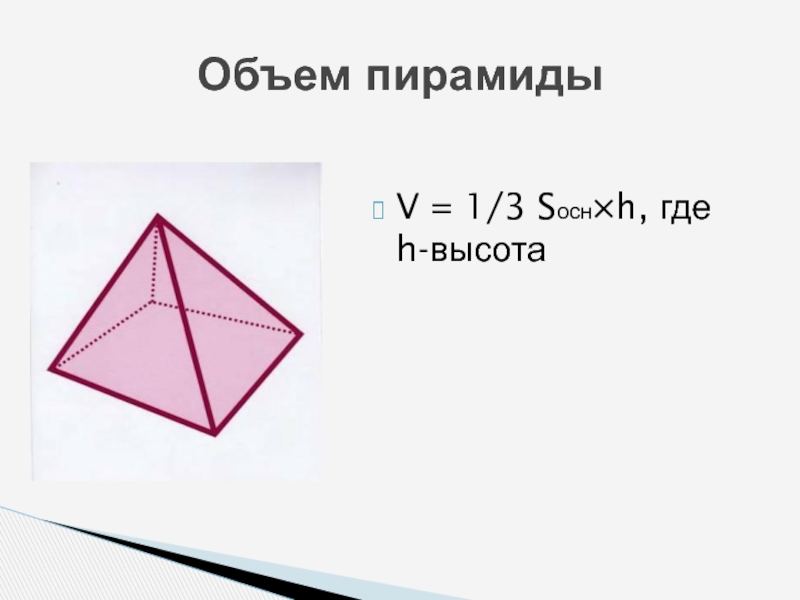
9. V = 1/3 Sосн×h, где h-высотаОбъем пирамиды
10. Прямоугольный параллелепипед
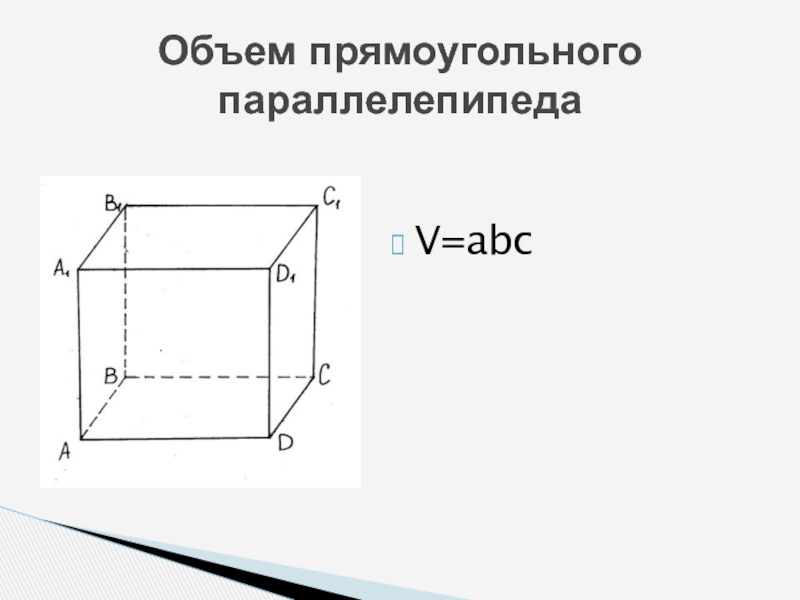
11. Объем прямоугольного параллелепипедаV=abc
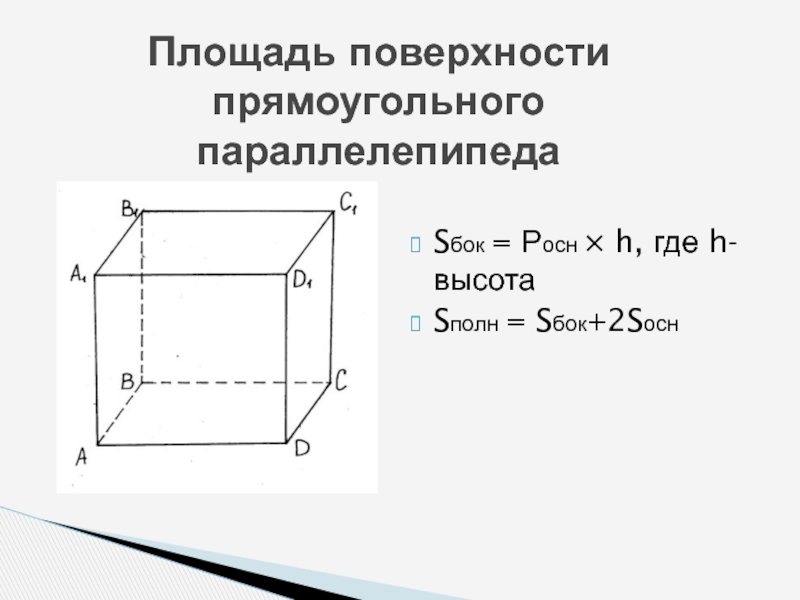
12. Площадь поверхности прямоугольного параллелепипедаSбок = Росн × h, где h-высотаSполн = Sбок+2Sосн
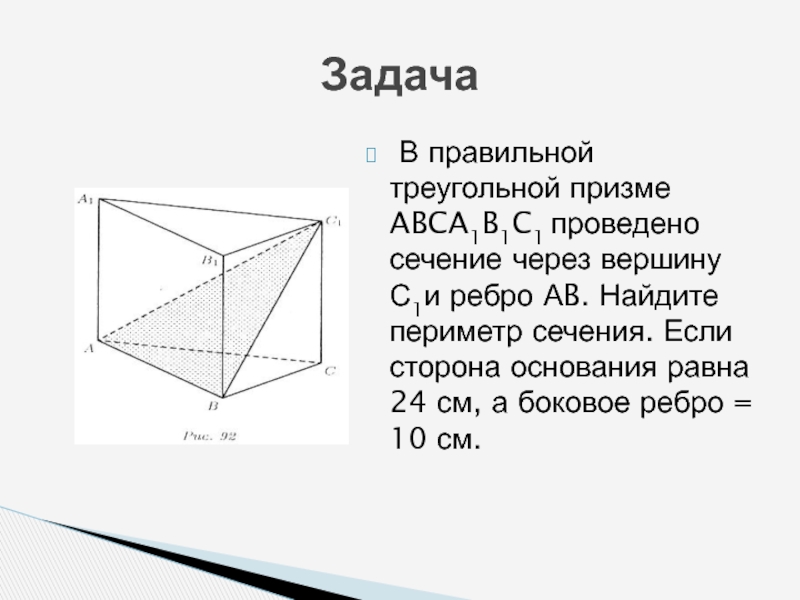
13. Задача В правильной треугольной призме ABCA1B1C1 проведено
14. Сечение ABC1 - равнобедренный треугольник, так какBC1

Поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, называется многогранником.Понятие многогранника

Главная
Геометрия
Презентация по математике на тему Многогранники

Слайд 1Многогранники
Выполнила:
учитель математики
МКОУ «Гремяченская СОШ»
Денисенко Л.А.

Многогранники Выполнила:учитель математикиМКОУ «Гремяченская СОШ» Денисенко Л.А.

Слайд 2Поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, называется многогранником.
Понятие

многогранника

Поверхность, составленная из многоугольников и ограничивающая некоторое геометрическое тело, называется многогранником.Понятие многогранника

Слайд 3Выпуклые и невыпуклые многогранники

Выпуклые и невыпуклые многогранники

Слайд 4Призма

Призма

Слайд 5Sбок=Росн×h, где h-высота
Sполн=Sбок+2Sосн

Площадь поверхности призмы

Sбок=Росн×h, где h-высотаSполн=Sбок+2SоснПлощадь поверхности призмы

Слайд 6V=Sосн×h, где h-высота

Объем призмы

V=Sосн×h, где h-высотаОбъем призмы

Слайд 7Пирамида

Пирамида

Слайд 8Sполн=Sбок+Sосн
Sбок=1/2 Pосн×d, где d- апофема

Площадь поверхности пирамиды

Sполн=Sбок+SоснSбок=1/2 Pосн×d, где d- апофемаПлощадь поверхности пирамиды

Слайд 9V = 1/3 Sосн×h, где h-высота

Объем пирамиды

V = 1/3 Sосн×h, где h-высотаОбъем пирамиды

Слайд 10Прямоугольный параллелепипед

Прямоугольный параллелепипед

Слайд 11Объем прямоугольного параллелепипеда
V=abc

Объем прямоугольного параллелепипедаV=abc

Слайд 12Площадь поверхности прямоугольного параллелепипеда
Sбок = Росн × h, где h-высота
Sполн =

Sбок+2Sосн

Площадь поверхности прямоугольного параллелепипедаSбок = Росн × h, где h-высотаSполн = Sбок+2Sосн

Слайд 13Задача
В правильной треугольной призме ABCA1B1C1 проведено сечение через вершину С1и

ребро АB. Найдите периметр сечения. Если сторона основания равна 24 см, а боковое ребро = 10 см.

Задача В правильной треугольной призме ABCA1B1C1 проведено сечение через вершину С1и ребро АB. Найдите периметр сечения. Если

Слайд 14Сечение ABC1 - равнобедренный треугольник, так как
BC1 = AC1
как диагонали боковых

граней (рис. 92). В правильной треугольной призме боковые ребра перпендикулярны основанию. Поэтому треугольник BCC1 -— прямоугольный и по теореме Пифагора

Таким образом, периметр сечения равен

Ответ. 76 см.

Сечение ABC1 - равнобедренный треугольник, так какBC1 = AC1как диагонали боковых граней (рис. 92). В правильной треугольной

Скачать презентацию

Что такое shareslide.ru?

Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.

Для правообладателей

Обратная связь

Email: Нажмите что бы посмотреть