- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Урок геометрии в 11 классе Площадь сферы
Содержание
- 1. Урок геометрии в 11 классе Площадь сферы
- 2. Мы с вами живем на планете Земля,
- 3. Если мы очистим яблоко, поверхность какой пощади можно покрыть его кожурой?
- 4. Сколько краски потребуется для того, чтобы покрасить какой-либо шарик?
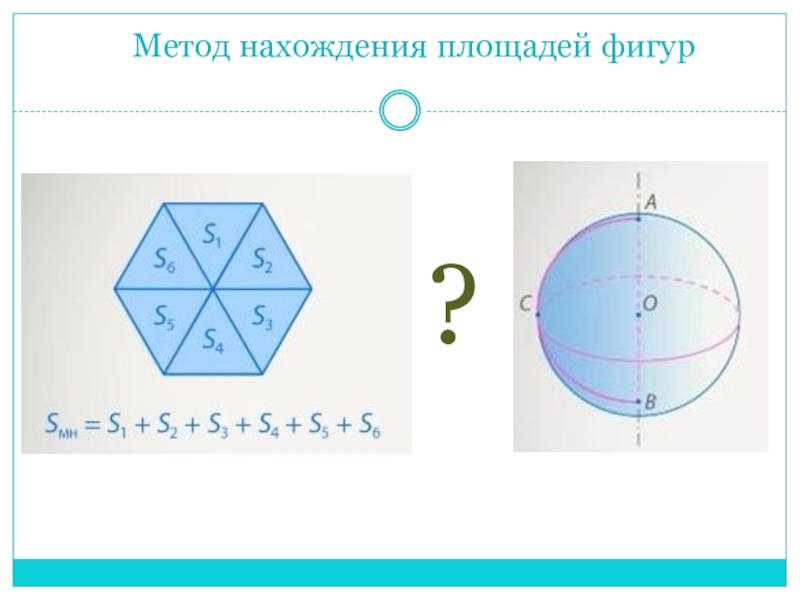
- 5. Метод нахождения площадей фигур ?
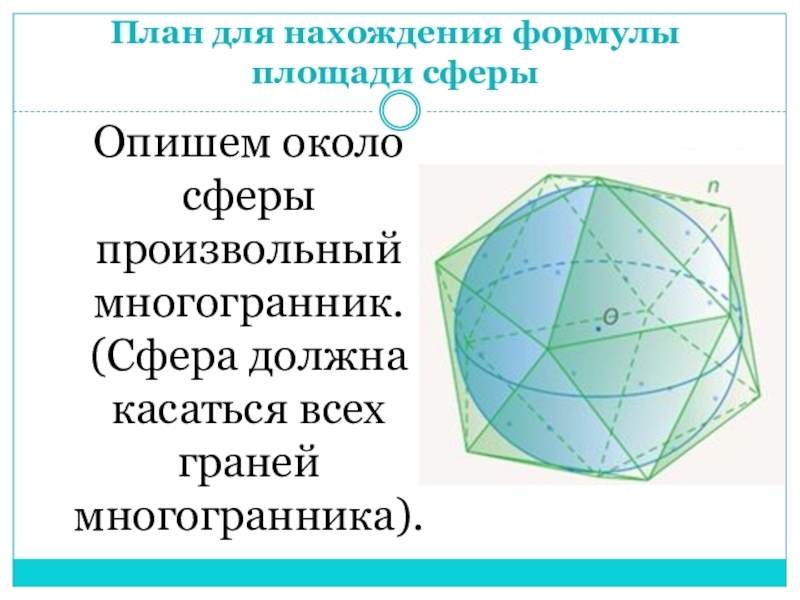
- 6. План для нахождения формулы площади сферыОпишем около сферы произвольный многогранник. (Сфера должна касаться всех граней многогранника).
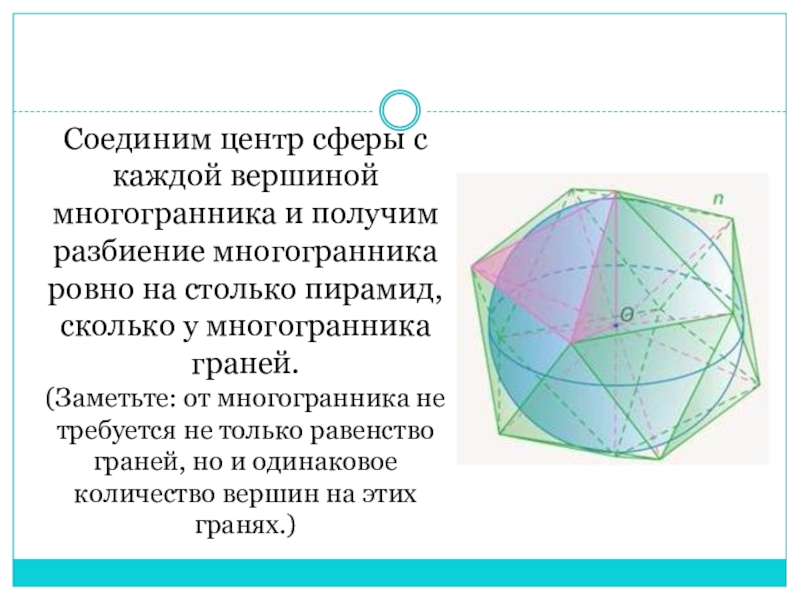
- 7. Соединим центр сферы с каждой вершиной многогранника
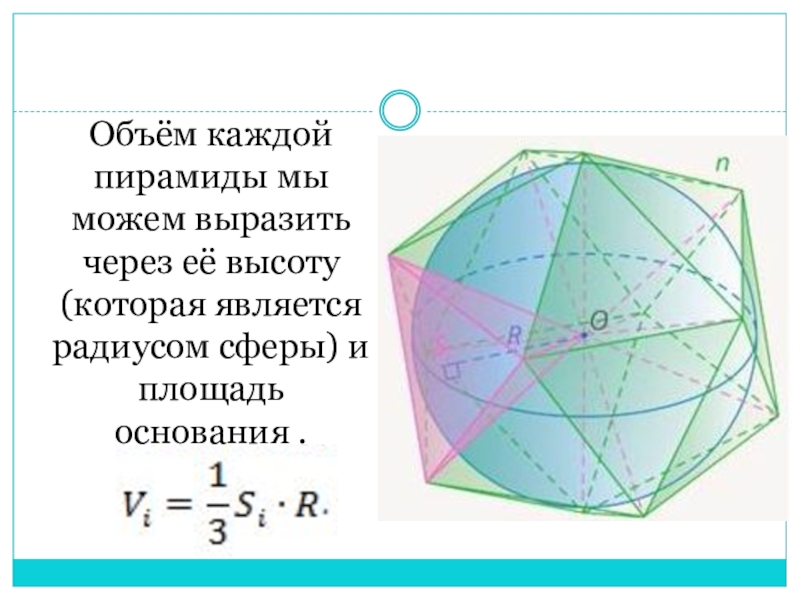
- 8. Объём каждой пирамиды мы можем выразить через её высоту (которая является радиусом сферы) и площадь основания .
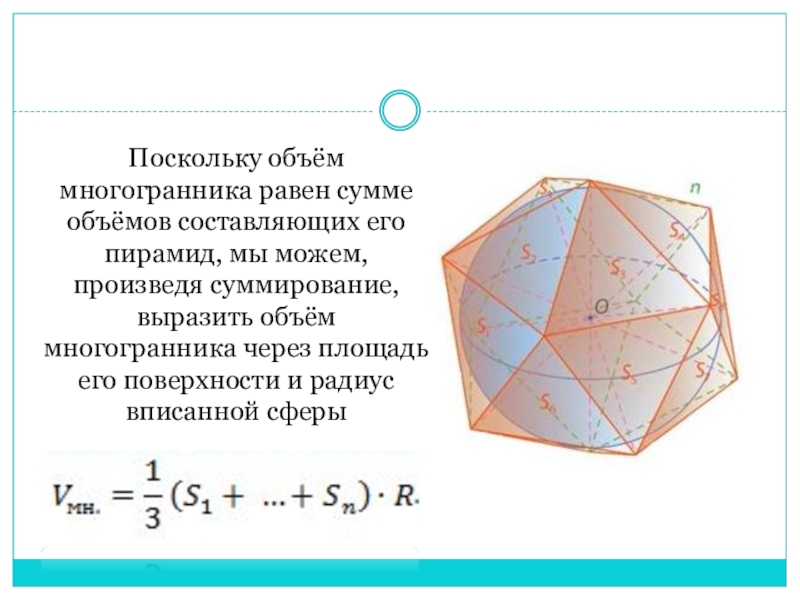
- 9. Поскольку объём многогранника равен сумме объёмов составляющих
- 10. А теперь станем неограниченно увеличивать количество граней
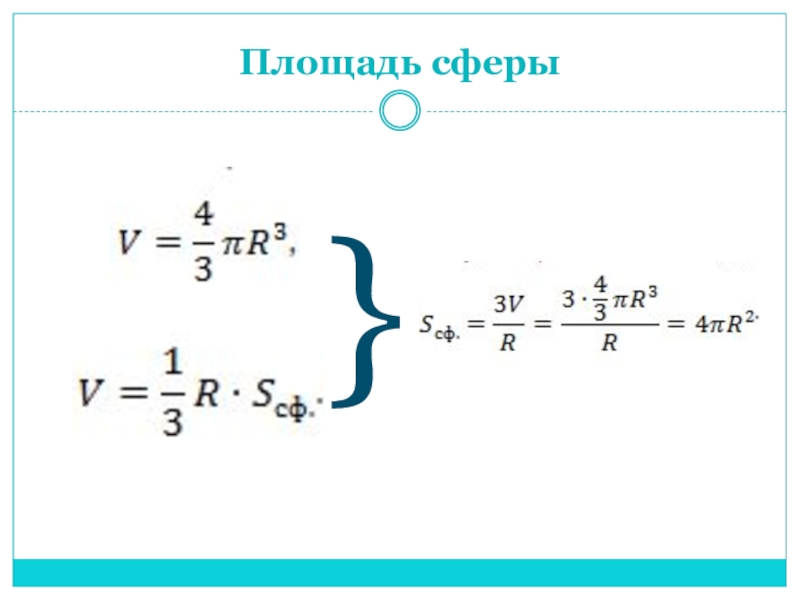
- 11. Площадь сферы}
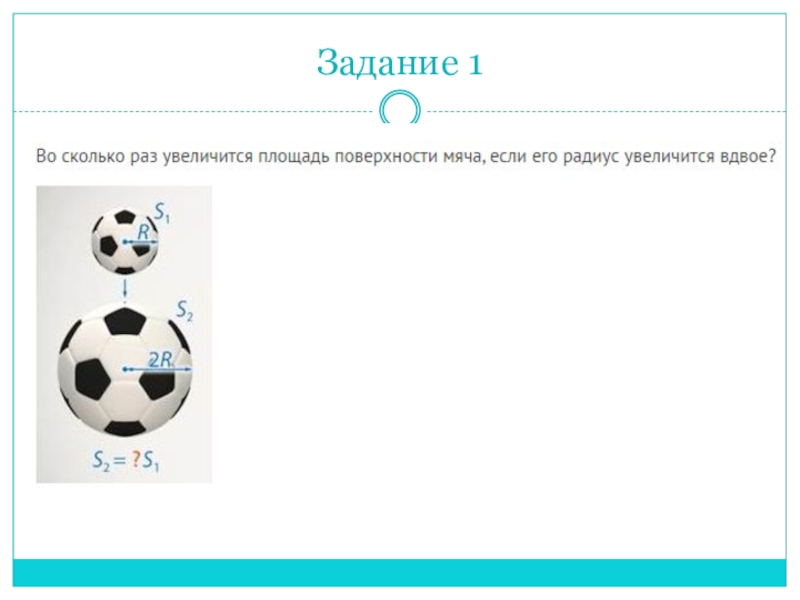
- 12. Задание 1
- 13. Заданий 2
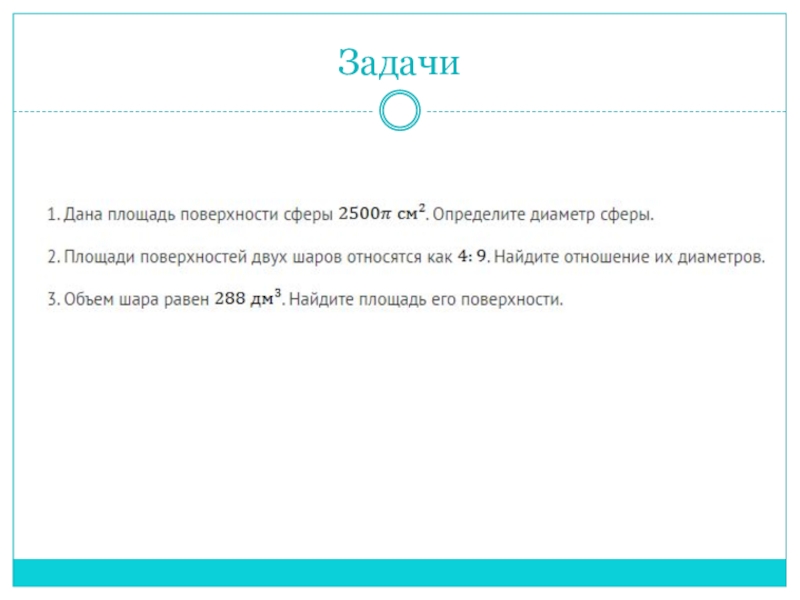
- 14. Задачи
Мы с вами живем на планете Земля, которая, с некоторыми допущениями, имеет форму шара. А сколько места на поверхности этой планеты?
Слайд 2Мы с вами живем на планете Земля, которая, с некоторыми допущениями,
имеет форму шара. А сколько места на поверхности этой планеты?
Слайд 6План для нахождения формулы площади сферы
Опишем около сферы произвольный многогранник. (Сфера
должна касаться всех граней многогранника).
Слайд 7Соединим центр сферы с каждой вершиной многогранника и получим разбиение многогранника
ровно на столько пирамид, сколько у многогранника граней.
(Заметьте: от многогранника не требуется не только равенство граней, но и одинаковое количество вершин на этих гранях.)
Слайд 8Объём каждой пирамиды мы можем выразить через её высоту (которая является
радиусом сферы) и площадь основания .
Слайд 9Поскольку объём многогранника равен сумме объёмов составляющих его пирамид, мы можем,
произведя суммирование, выразить объём многогранника через площадь его поверхности и радиус вписанной сферы
Слайд 10А теперь станем неограниченно увеличивать количество граней многогранника, одновременно уменьшая размеры
самой большой из них. Тогда в пределе многогранник перейдёт в шар, а зависимость между его объёмом и площадью поверхности станет зависимостью между объёмом шара и площадью поверхности сферы.