- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему: Правильные многогранники
Содержание
- 1. Презентация по математике на тему: Правильные многогранники
- 2. Цель урока: ознакомление студентов с правильными многогранниками,
- 3. Мир многогранниковМногогранники окружают нас в повседневной жизни
- 4. Правильные многогранникиСколько же их существует? Рассмотрим развертку
- 5. Теперь перейдем к квадратным граням. Развертка из
- 6. Многогранник называется правильным, если все его грани
- 7. огоньтетраэдрикосаэдр октаэдр гексаэдрвселеннаядодекаэдрводаземлявоздухНачиная с 7 века до
- 8. Выпуклые правильные многогранники принято называть Платоновы
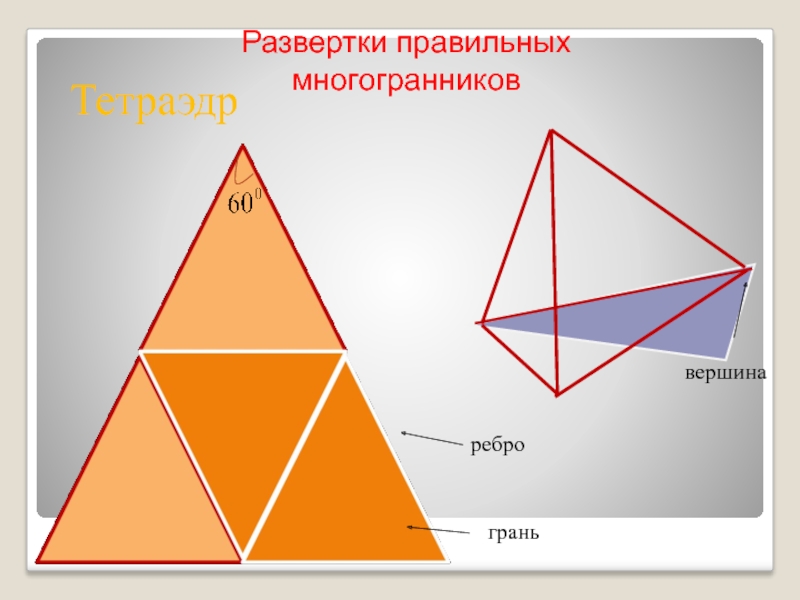
- 9. вершинареброграньТетраэдрРазвертки правильных многогранников
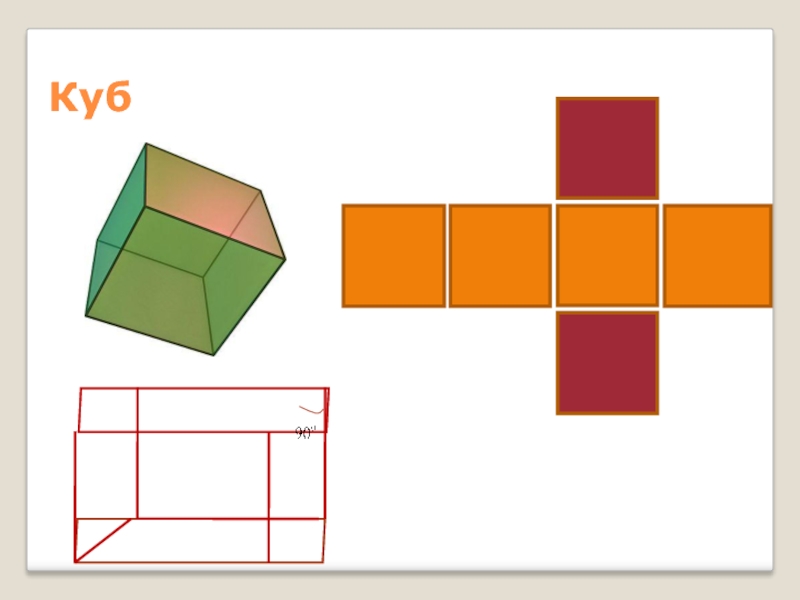
- 10. Куб
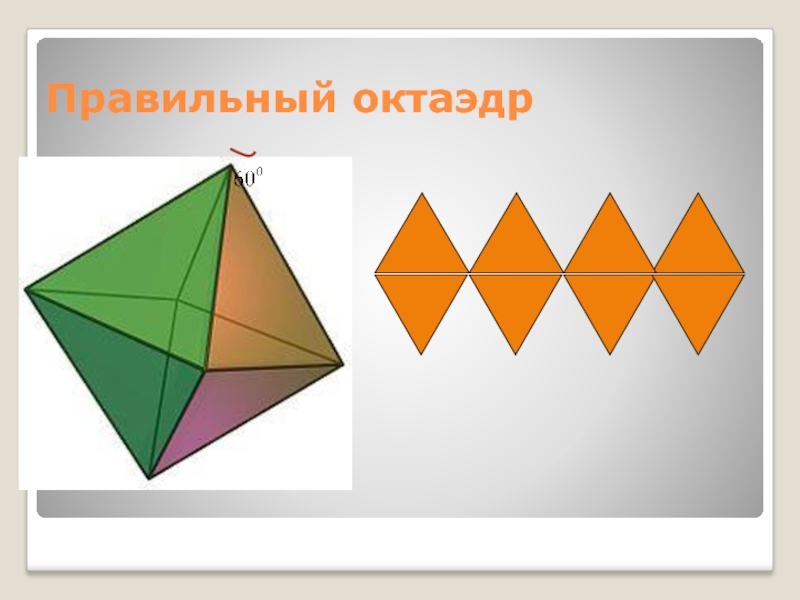
- 11. Правильный октаэдр
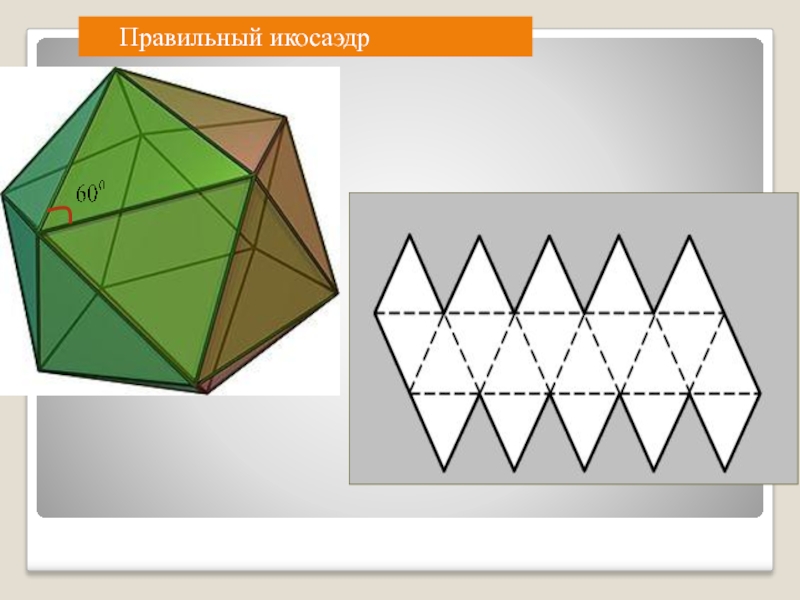
- 12. Правильный икосаэдр
- 13. Слайд 13
- 14. Тетраэдр446Куб8612Октаэдр6812Икосаэдр122030Додекаэдр20123022222 В+Г-Р = 2формула Эйлера
- 15. Число =В+Г-Р называется эйлеровой характеристикой многогранника. Согласно
- 16. Сколько граней, ребер и вершин имеет n-угольная
- 17. n+2; 3n; 2nНетНетОдноЧетыреКубПрямоугольный параллелепипедТреугольная призма; пять гранейДодекаэдрВысотаОтветы на вопросы
- 18. Материалы:Литература .Атанасян Л.С. Геометрия: Учеб. для 10-11
Слайд 1Тема урока:
Правильные многогранники
ГБПОУ РМ «Рузаевский политехнический техникум»
Преподаватель математики Курочкина В.М.
Слайд 2Цель урока: ознакомление студентов с правильными многогранниками, их характеристиками
Задачи:
Обучающие:
Ввести понятие
Рассмотреть свойства правильных многогранников.
Развивающие:
Формирование пространственных представлений.
Формирование умения обобщать, систематизировать, видеть закономерности.
Развитие монологической речи.
Воспитательные:
Воспитание эстетического чувства.
Воспитание умения слушать.
Формирование интереса к предмету.
Оборудование:
экран, проектор, компьютер
Слайд 3Мир многогранников
Многогранники окружают нас в
повседневной жизни ежедневно:
спичечный коробок,
книга,
различные архитектурные сооружения.
Слайд 4Правильные многогранники
Сколько же их существует?
Рассмотрим развертку вершины многогранника. Каждая вершина
Сначала рассмотрим случай, когда грани многогранника - равносторонние треугольники. Поскольку внутренний угол равностороннего треугольника равен 60°, три таких угла дадут в развертке 180°. Если теперь склеить развертку в многогранный угол, получится тетраэдр - многогранник, в каждой вершине которого встречаются три правильные треугольные грани. Если добавить к развертке вершины еще один треугольник, в сумме получится 240°. Это развертка вершины октаэдра. Добавление пятого треугольника даст угол 300° - мы получаем развертку вершины икосаэдра. Если же добавить еще один, шестой треугольник, сумма углов станет равной 360° - эта развертка, очевидно, не может соответствовать ни одному выпуклому многограннику.
Слайд 5Теперь перейдем к квадратным граням. Развертка из трех квадратных граней имеет
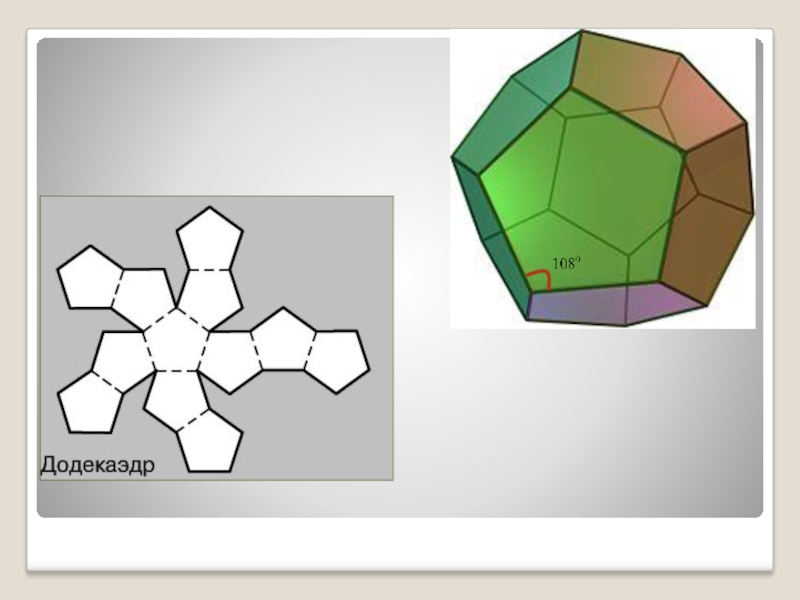
Три пятиугольные грани дают угол развертки 3*108°=324 - вершина додекаэдра. Если добавить еще один пятиугольник, получим больше 360° - поэтому останавливаемся.
Для шестиугольников уже три грани дают угол развертки 3*120°=360°, поэтому правильного выпуклого многогранника с шестиугольными гранями не существует. Если же грань имеет еще больше углов, то развертка будет иметь еще больший угол. Значит, правильных выпуклых многогранников с гранями, имеющими шесть и более углов, не существует.
Слайд 6 Многогранник называется правильным, если все его грани – правильные многоугольники и
Существует пять видов правильных многогранников:
Тетраэдр – состоит из четырех правильных треугольников, в каждой вершине сходится по три ребра.
Куб – состоит из шести квадратов, в каждой вершине сходится по три ребра.
Октаэдр – состоит из восьми правильных треугольников, в каждой вершине сходится по четыре ребра.
Икосаэдр - состоит из 20 правильных треугольников, в каждой вершине сходится по пять ребер.
Додекаэдр - состоит из 12 правильных пятиугольников, в каждой вершине сходится по три ребра.
Сделаем вывод:
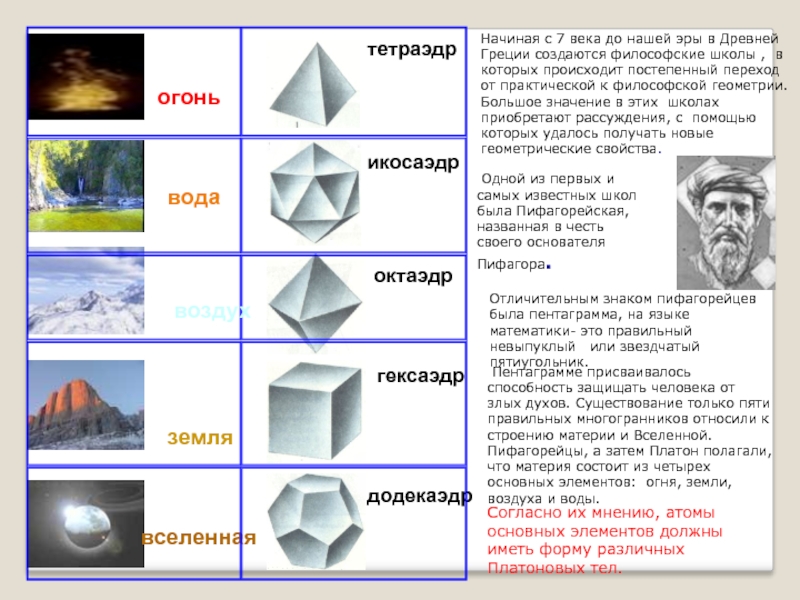
Слайд 7 огонь
тетраэдр
икосаэдр
октаэдр
гексаэдр
вселенная
додекаэдр
вода
земля
воздух
Начиная с 7 века до нашей эры в Древней
Одной из первых и самых известных школ была Пифагорейская, названная в честь своего основателя Пифагора.
Отличительным знаком пифагорейцев была пентаграмма, на языке математики- это правильный невыпуклый или звездчатый пятиугольник.
Пентаграмме присваивалось способность защищать человека от злых духов. Существование только пяти правильных многогранников относили к строению материи и Вселенной. Пифагорейцы, а затем Платон полагали, что материя состоит из четырех основных элементов: огня, земли, воздуха и воды.
Согласно их мнению, атомы основных элементов должны иметь форму различных Платоновых тел.
Слайд 8
Выпуклые правильные многогранники принято называть Платоновы тела.
Древнегреческий философ Платон
Они были известны задолго до Платона. При раскопках была найдена модель додекаэдра, служившая детской игрушкой более 2500 лет назад.
Слайд 15Число =В+Г-Р называется эйлеровой характеристикой многогранника. Согласно теореме Эйлера, для выпуклого
Слайд 16Сколько граней, ребер и вершин имеет n-угольная призма?
Может ли боковая грань
Может ли в основании правильной пирамиды лежать прямоугольный треугольник?
Сколько боковых ребер у пирамиды могут быть перпендикулярны основанию?
Сколько диагоналей имеет параллелепипед?
Как называется иначе правильная четырехугольная призма, все ребра которой равны?
Каким многогранником является кирпич?
Какая призма имеет меньшее число граней и сколько их?
Какой правильный многогранник имеет 12 граней?
Как называется расстояние между основаниями призмы?
Вопросы по теме
Слайд 17n+2; 3n; 2n
Нет
Нет
Одно
Четыре
Куб
Прямоугольный параллелепипед
Треугольная призма; пять граней
Додекаэдр
Высота
Ответы на вопросы
Слайд 18Материалы:
Литература .
Атанасян Л.С. Геометрия: Учеб. для 10-11 кл. общеобразоват. учреждений.
/
2. Саакян С.М. Изучение темы «Многогранники» в курсе 10 класса. / С.М. Саакян, В.Ф. Бутузов.
// Математика в школе. – 2000. - № 2.
3.Шарыгин И.Ф.: «Наглядная геометрия» /И.Ф. Шарыгин, Л.Н. Ерганжиева -М.: МИРОС,1992.- 41с.
2. Интернет- ссылки
http://ru.wikipedia.org/wiki/Додекаэдр
http://ru.wikipedia.org/wiki/Октаэдр
http://ru.wikipedia.org/wiki/Икосаэдр
http://ru.wikipedia.org/wiki/Эйлер,_Леонард
http://mkesher.chat.ru/cub.htm
http://vergesso.my1.ru/photo/2-0-1