Презентация, доклад на тему Учебная презентация по теме Применение подобия

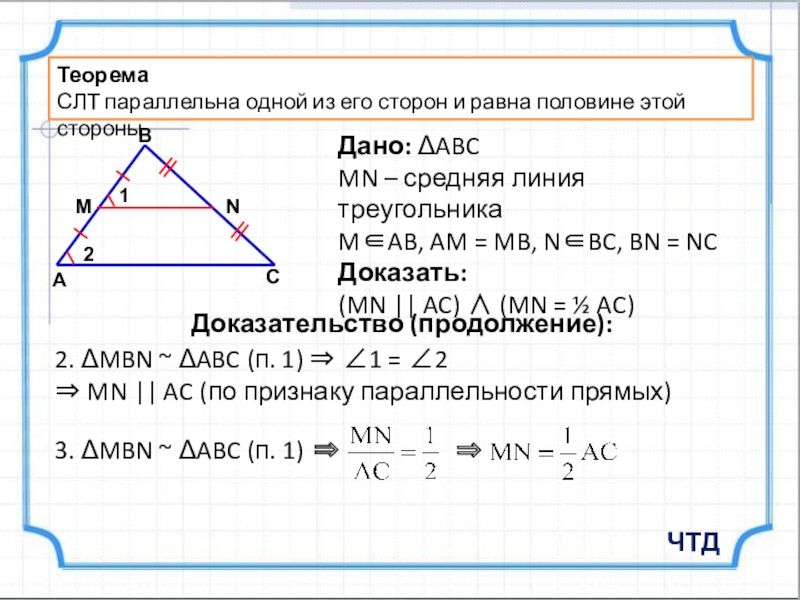
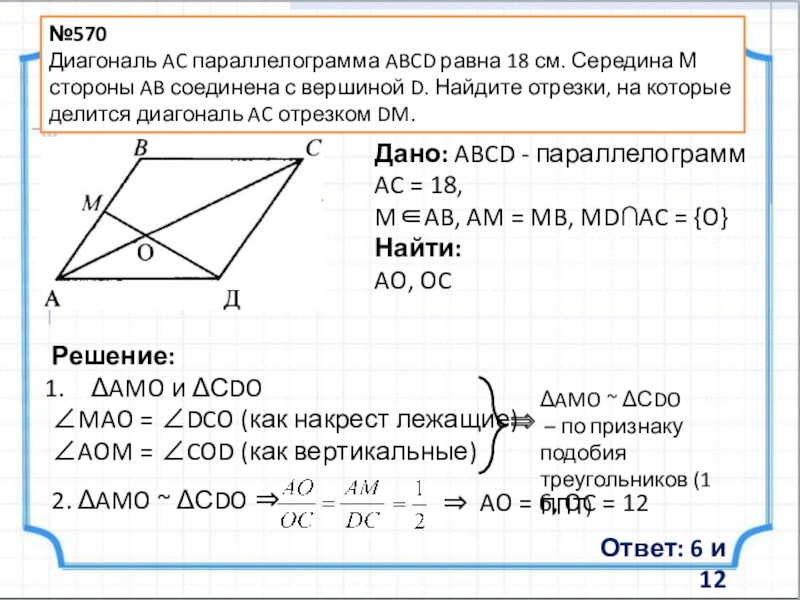
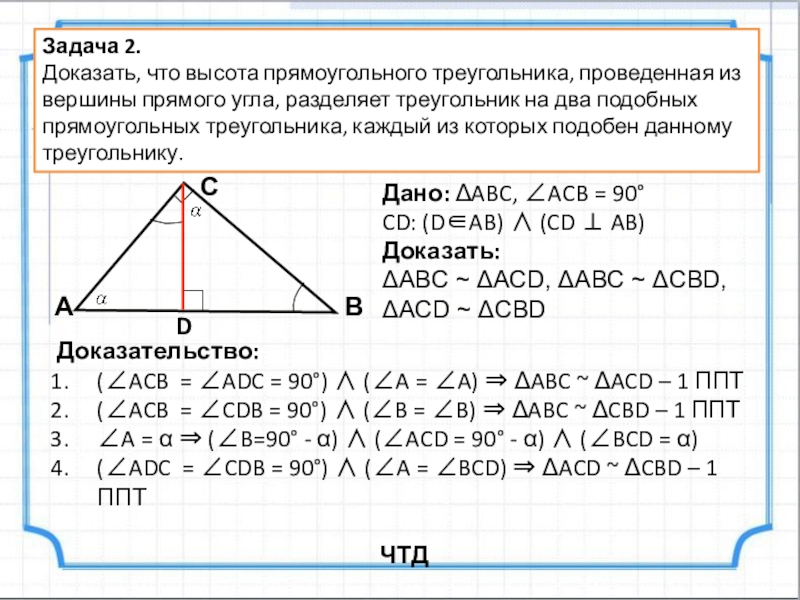
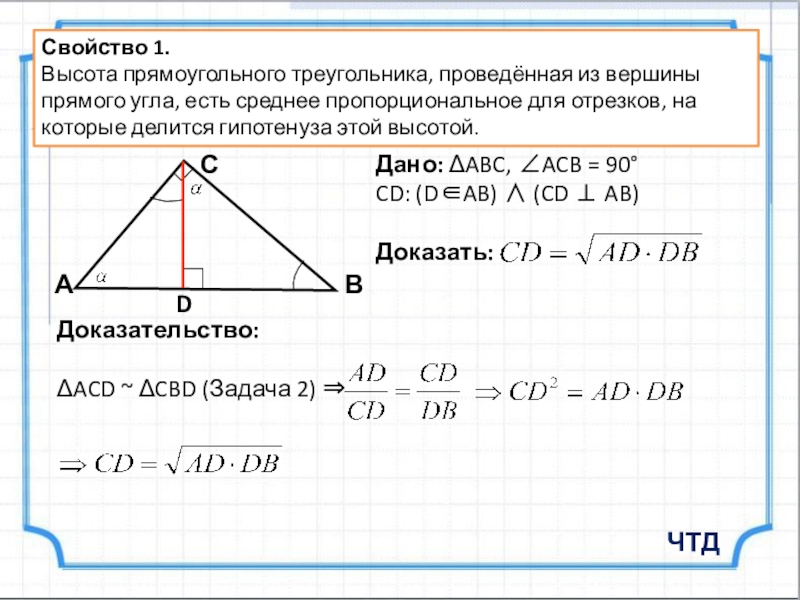
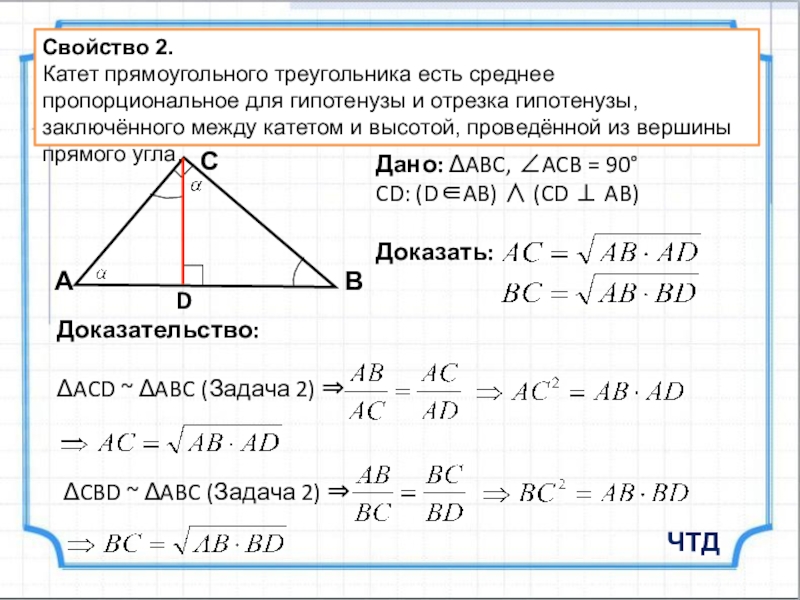
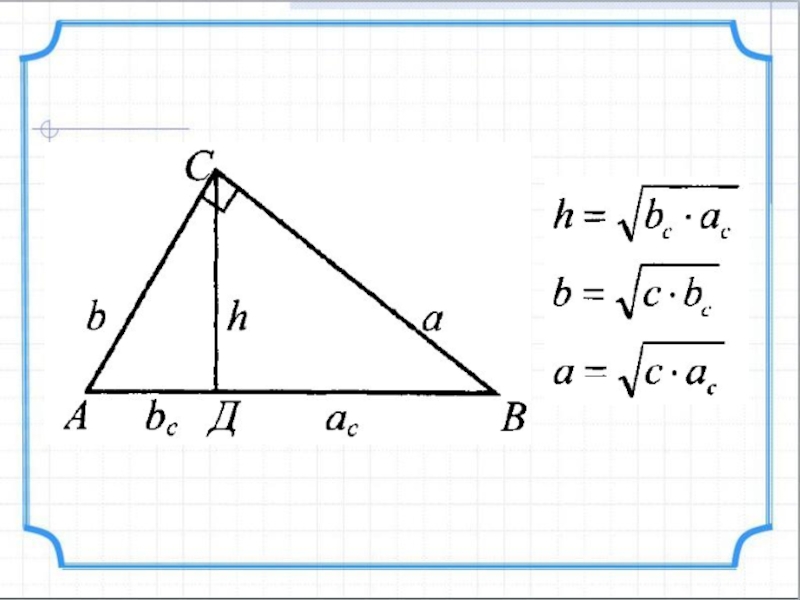
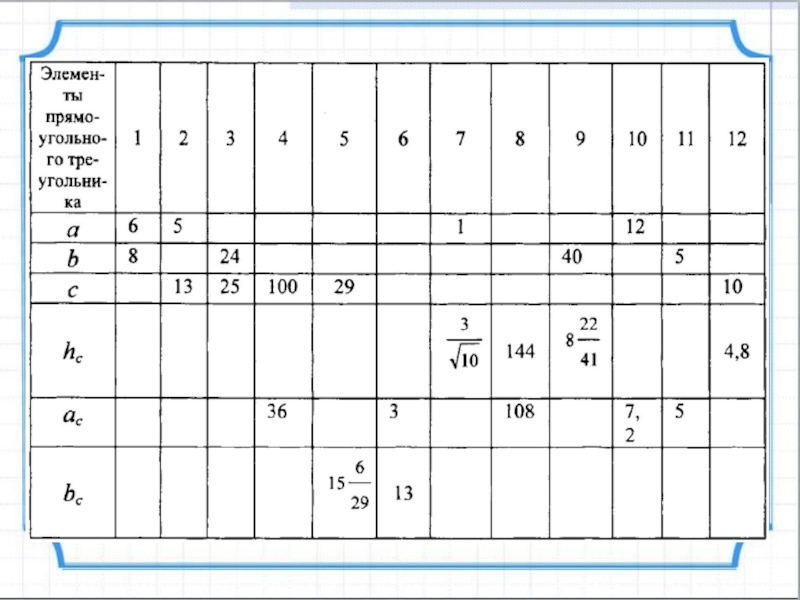
Дано: ABC
MN – средняя линия треугольника
MAB, AM = MB, NBC, BN = NC
Доказать:
(MN || AC)  (MN = ½ AC)

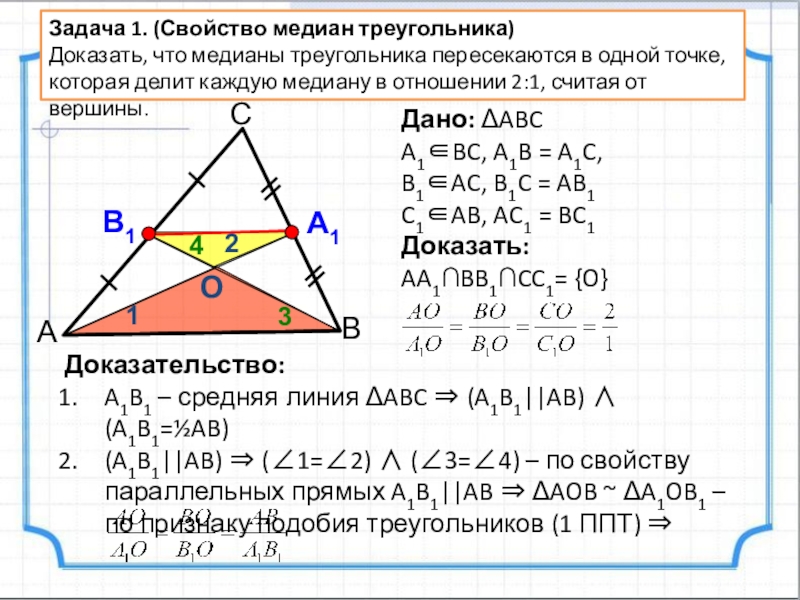
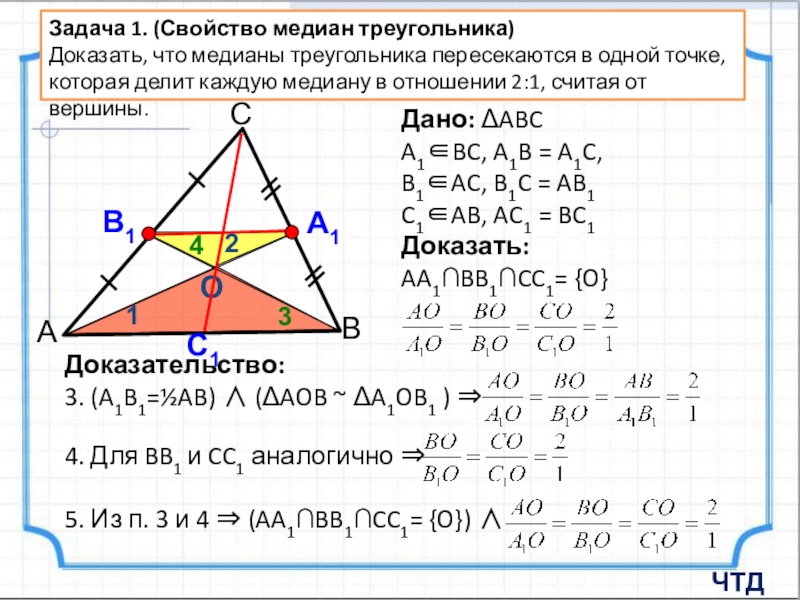
Доказательство:

- Отрезок, соединяющий середины двух его сторон.

1. MBN и ABC
B = B

- По условию



MBN ~ ABC – по признаку подобия треугольников (2 ППТ)

1

2

Доказательство (продолжение):



2. MBN ~ ABC (п. 1)  1 = 2
 MN || AC (по признаку параллельности прямых)

1

2

3. MBN ~ ABC (п. 1)



ЧТД

Доказательство:
(MAD, AM = MD)  (NAB, AN = NB)  MN – средняя линия ABD  (MN || BD)  (MN = ½ BD)
(PBC, BP = PC)  (QDC, DQ = QC)  PQ – средняя линия BDC  (QP || BD)  (QP = ½ BD)
(MN || BD)  (QP || BD) – п.1, 2  (QP || MN)
(MN = ½ BD)  (QP = ½ BD) – п.1, 2  (QP = MN)
(QP || MN)  (QP = MN)  MNPQ – параллелограмм

ЧТД

А

С

В

Дано: ABC
A1BC, A1B = A1C,
B1AC, B1C = AB1
C1AB, AC1 = BC1
Доказать:
AA1BB1CC1= {O}

Доказательство:
A1B1 – средняя линия ABC  (A1B1||AB)  (A1B1=½AB)
(A1B1||AB)  (1=2)  (3=4) – по свойству параллельных прямых A1B1||AB  AOB ~ A1OB1 – по признаку подобия треугольников (1 ППТ) 

А

С

В

Доказательство:
3. (A1B1=½AB)  (AOB ~ A1OB1 ) 

Дано: ABC
A1BC, A1B = A1C,
B1AC, B1C = AB1
C1AB, AC1 = BC1
Доказать:
AA1BB1CC1= {O}

4. Для BB1 и CC1 аналогично 

5. Из п. 3 и 4  (AA1BB1CC1= {O}) 

ЧТД

С1

Дано: ABCD - параллелограмм
AC = 18,
MAB, AM = MB, MDAC = {O}
Найти:
AO, OC

Решение:
AMO и СDO
MAO = DCO (как накрест лежащие)
AOM = COD (как вертикальные)



AMO ~ СDO
– по признаку подобия треугольников (1 ППТ)

2. AMO ~ СDO 



AO = 6, OC = 12

Ответ: 6 и 12

# Отрезок длиной 6 см является средним пропорциональным
между отрезками с длинами 9 см и 4 см, т.к. 9 : 6 = 6 : 4.

а : х = х : в  х2 = а  в 

1. Является ли отрезок длиной 8 см средним пропорциональным между отрезками с длинами 16 см и 4 см ?

2. Является ли отрезок длиной 9 см средним пропорциональным
между отрезками с длинами 15 см и 6 см ?

да

нет

да

х – среднее геометрическое между а и в

Дано: ABC, ACB = 90
CD: (DAB)  (CD  AB)
Доказать:
ABC ~ ACD, ABC ~ CBD, ACD ~ CBD

Доказательство:
(ACB = ADC = 90)  (A = A)  ABC ~ ACD – 1 ППТ
(ACB = CDB = 90)  (B = B)  ABC ~ CBD – 1 ППТ
A =   (B=90 - )  (ACD = 90 - )  (BCD = )
(ADC = CDB = 90)  (A = BCD)  ACD ~ CBD – 1 ППТ

ЧТД

Дано: ABC, ACB = 90
CD: (DAB)  (CD  AB)

Доказать:

Доказательство:

ACD ~ CBD (Задача 2) 

ЧТД

Дано: ABC, ACB = 90
CD: (DAB)  (CD  AB)

Доказать:

Доказательство:

ACD ~ ABC (Задача 2) 

CBD ~ ABC (Задача 2) 

ЧТД