- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Учебная презентация по теме Касательная к окружности
Содержание
- 1. Учебная презентация по теме Касательная к окружности
- 2. I. Взаимное расположение прямой и окружностиВыясним, сколько
- 3. II. Прямая не проходит через центр окружностиДано:
- 4. Дано: ω (O, r) – окружность с
- 5. Дано: ω (O, r) – окружность с
- 6. Дано: ω (O, r) – окружность с
- 7. II. Касательная у окружностиПрямая, имеющая с окружностью
- 8. Касательные, проходящие через одну точкуТеорема (свойство):Отрезки касательных
- 9. Теорема (признак касательной)Если прямая проходит через конец
- 10. ЗадачаЧерез данную точку А окружности с центром
- 11. № 636Через концы хорды AB, равной радиусу
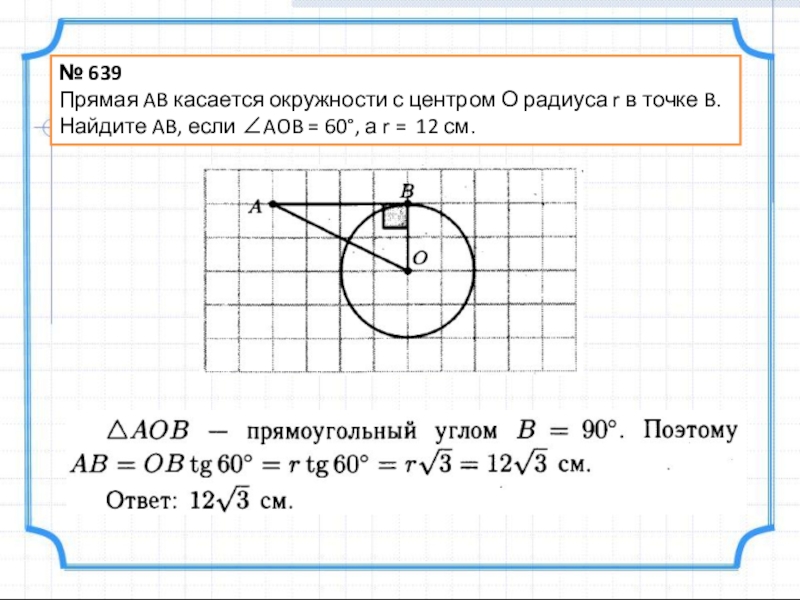
- 12. № 639Прямая AB касается окружности с центром
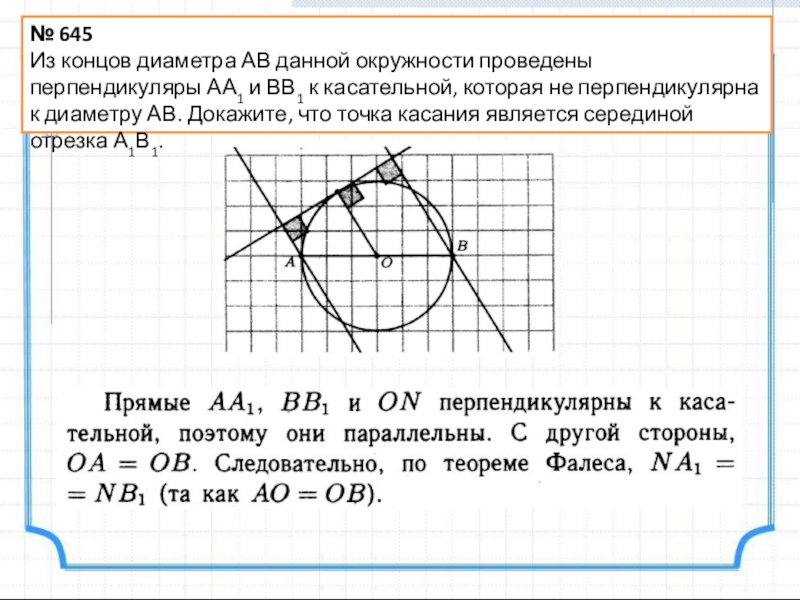
- 13. № 645Из концов диаметра АВ данной окружности
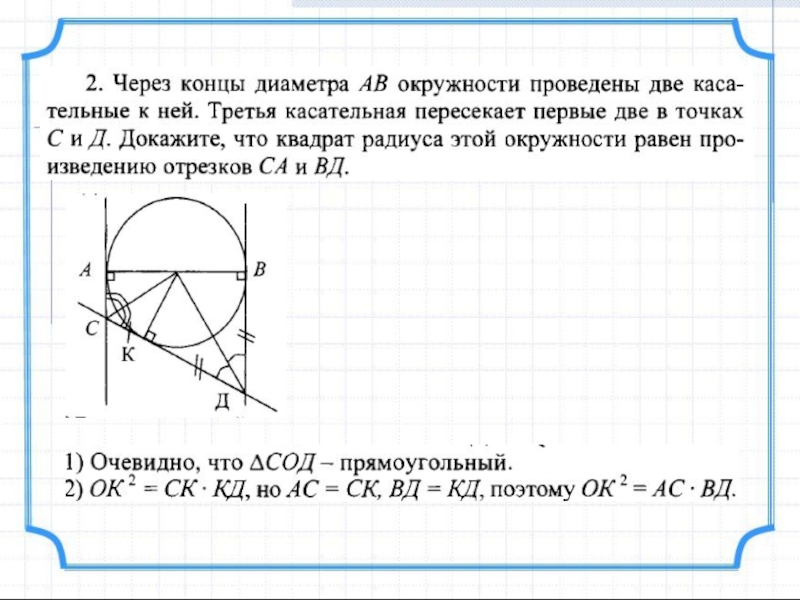
- 14. Слайд 14
- 15. Слайд 15
- 16. IV. Самостоятельная работа
- 17. Домашнее задание*70-71634, 638, 640
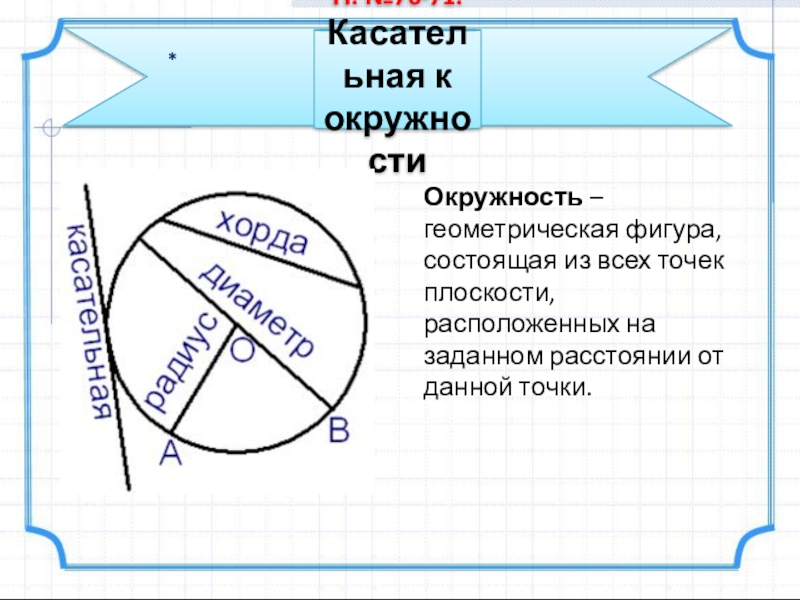
Слайд 1Окружность –
геометрическая фигура, состоящая из всех точек плоскости, расположенных на
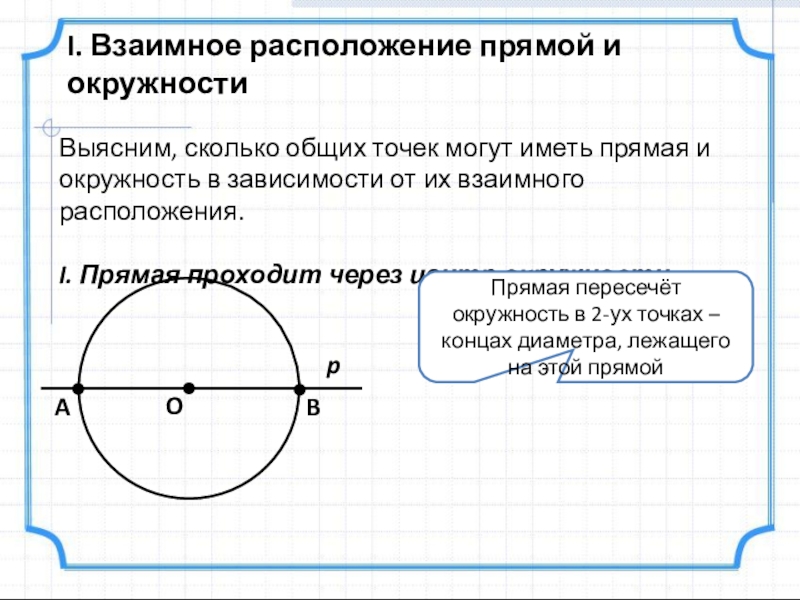
Слайд 2I. Взаимное расположение прямой и окружности
Выясним, сколько общих точек могут иметь
I. Прямая проходит через центр окружности
p
Прямая пересечёт окружность в 2-ух точках – концах диаметра, лежащего на этой прямой
Слайд 3II. Прямая не проходит через центр окружности
Дано:
ω (O, r) –
прямая p: O ∉ p,
OH ⊥ p, |OH| = d
p
1.
d < r
Слайд 4Дано:
ω (O, r) – окружность с центром в т. О
прямая p: O ∉ p,
OH ⊥ p, |OH| = d
p
1.
d < r
Докажем, что прямая p и окружность не имеют других общих точек.
Метод от противного:
Пусть ∃ т. C: (С∈ω) ∧ (С ∈ p)
ΔOAC: (OD – медиана)∧(D∈AC)
⇒OD ⊥ p
Т.О. из точки О проведены 2 перпендикуляра к прямой p - Противоречие
d < r ⇒ прямая и окружность имеют две общие точки
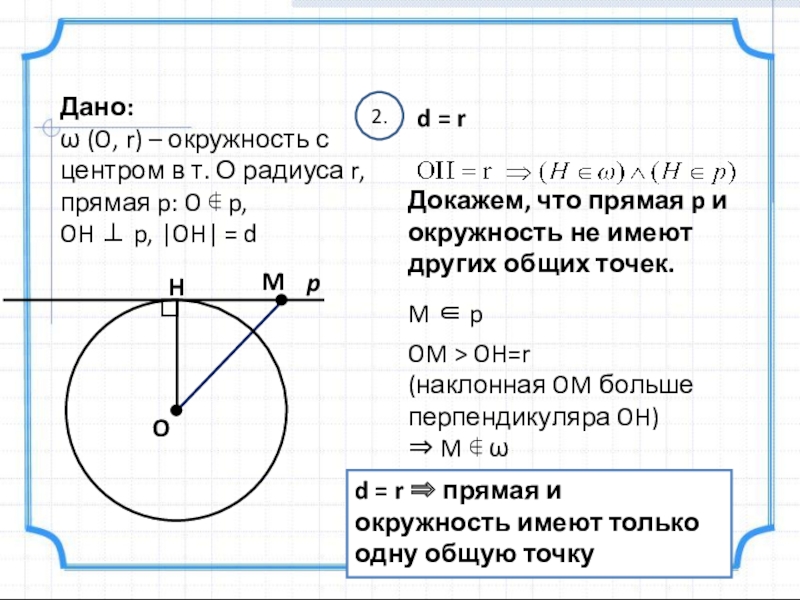
Слайд 5Дано:
ω (O, r) – окружность с центром в т. О
прямая p: O ∉ p,
OH ⊥ p, |OH| = d
2.
d = r
Докажем, что прямая p и окружность не имеют других общих точек.
M ∈ p
OM > OH=r
(наклонная OM больше перпендикуляра OH)
⇒ M ∉ ω
d = r ⇒ прямая и окружность имеют только одну общую точку
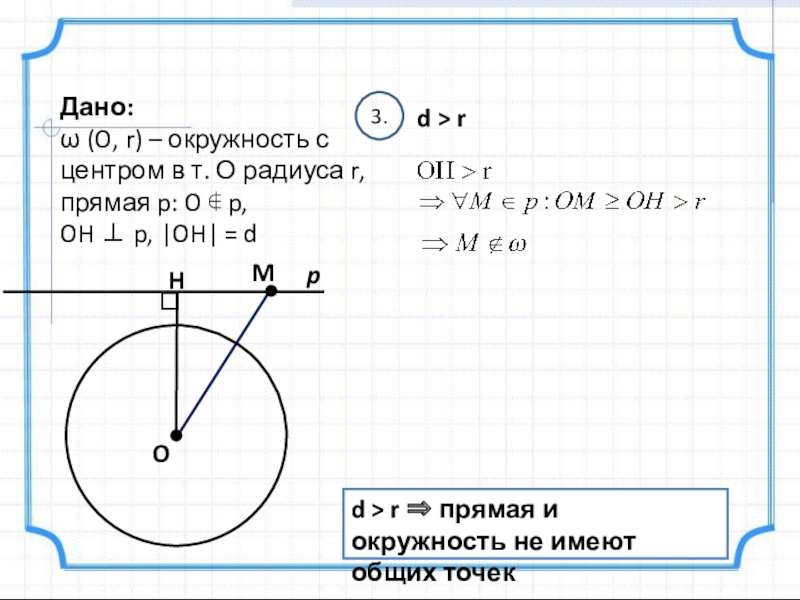
Слайд 6Дано:
ω (O, r) – окружность с центром в т. О
прямая p: O ∉ p,
OH ⊥ p, |OH| = d
3.
d > r
d > r ⇒ прямая и окружность не имеют общих точек
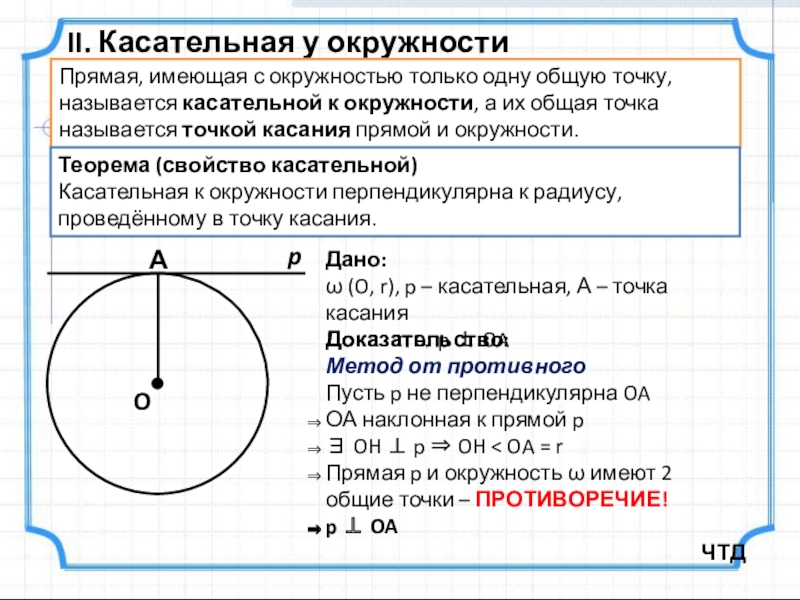
Слайд 7II. Касательная у окружности
Прямая, имеющая с окружностью только одну общую точку,
Теорема (свойство касательной)
Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
Дано:
ω (O, r), p – касательная, А – точка касания
Доказать: p ⊥ OA
Доказательство:
Метод от противного
Пусть p не перпендикулярна OA
ОА наклонная к прямой p
∃ OH ⊥ p ⇒ OH < OA = r
Прямая p и окружность ω имеют 2 общие точки – ПРОТИВОРЕЧИЕ!
p ⊥ OA
ЧТД
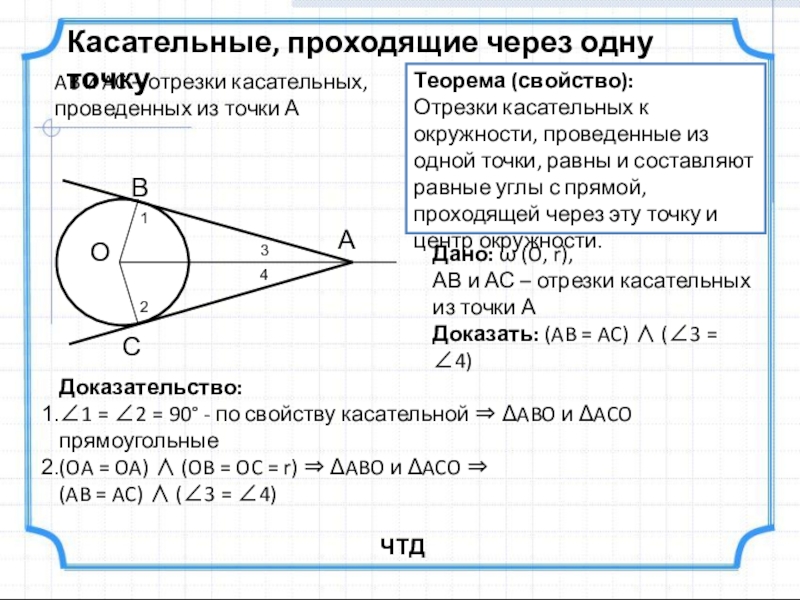
Слайд 8Касательные, проходящие через одну точку
Теорема (свойство):
Отрезки касательных к окружности, проведенные из
О
В
С
А
1
2
3
4
AB и AC – отрезки касательных, проведенных из точки А
Дано: ω (O, r),
АВ и АС – отрезки касательных из точки А
Доказать: (AB = AC) ∧ (∠3 = ∠4)
Доказательство:
∠1 = ∠2 = 90° - по свойству касательной ⇒ ΔABO и ΔACO прямоугольные
(OA = OA) ∧ (OB = OC = r) ⇒ ΔABO и ΔACO ⇒
(AB = AC) ∧ (∠3 = ∠4)
ЧТД
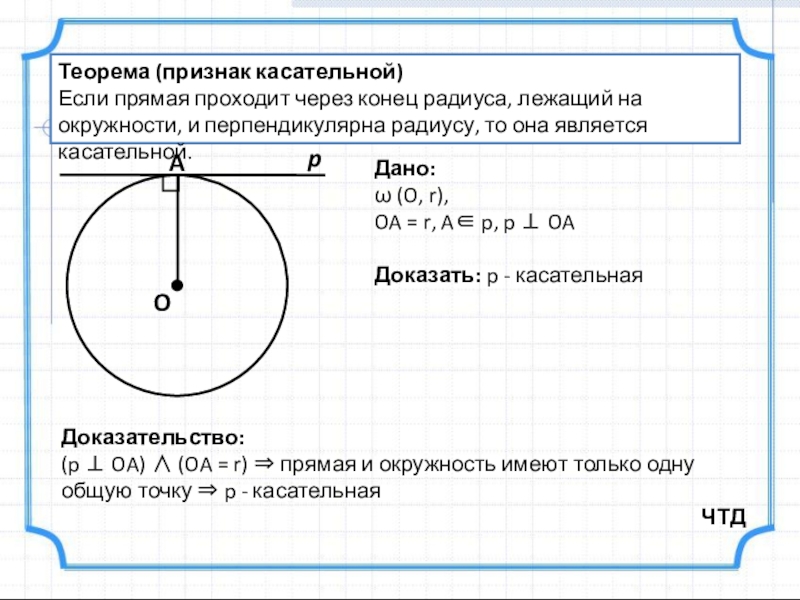
Слайд 9Теорема (признак касательной)
Если прямая проходит через конец радиуса, лежащий на окружности,
Дано:
ω (O, r),
OA = r, A∈ p, p ⊥ OA
Доказать: p - касательная
Доказательство:
(p ⊥ OA) ∧ (OA = r) ⇒ прямая и окружность имеют только одну общую точку ⇒ p - касательная
ЧТД
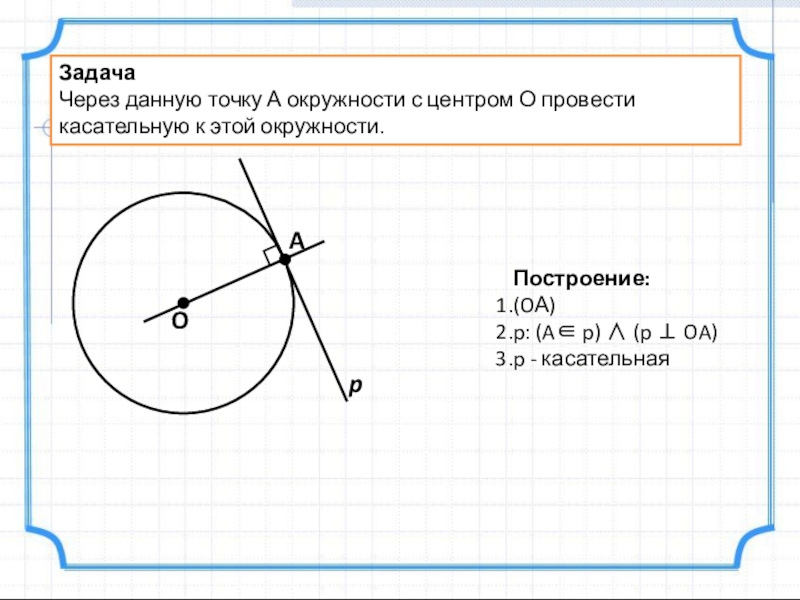
Слайд 10Задача
Через данную точку А окружности с центром О провести касательную к
Построение:
(OА)
p: (A∈ p) ∧ (p ⊥ OA)
p - касательная
Слайд 11№ 636
Через концы хорды AB, равной радиусу окружности, проведены две касательные,
III. Решение задач