- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Творческий проект учащихся к бинарному уроку Сечения многогранников. Построение сечений многогранников в программе Флипчарт. Оформление отчета выполненной работы в Word”
Содержание
- 1. Творческий проект учащихся к бинарному уроку Сечения многогранников. Построение сечений многогранников в программе Флипчарт. Оформление отчета выполненной работы в Word”
- 2. Цель проекта:Исследование сечений многогранников и анализ полученных результатов.
- 3. метод следов Методы построения сечений многогранников
- 4. Слайд 4
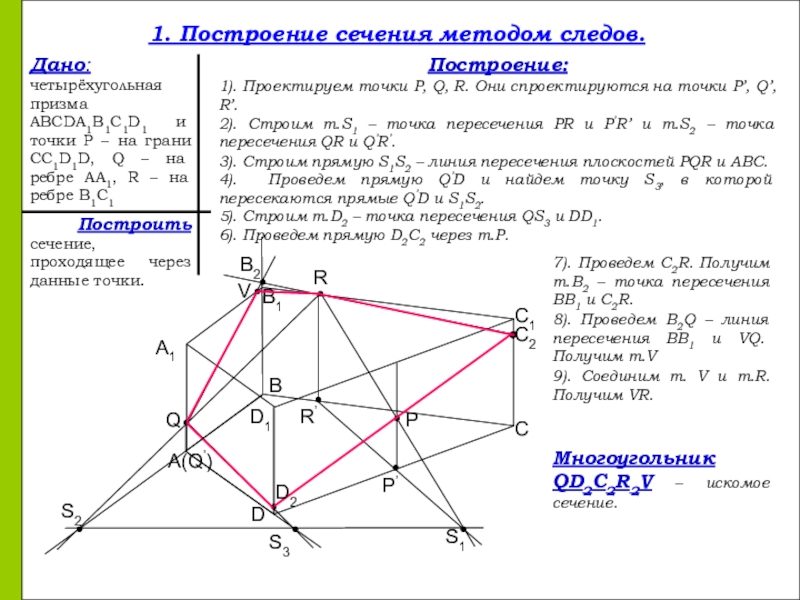
- 5. A1(Q’)QRPC1C2CDD1BB1R’P’S1S2S3VB21. Построение сечения методом следов.Дано: четырёхугольная призма
- 6. Метод внутреннего проектированияСущность метода внутреннего проектирования
- 7. AA1BB1CC1DD1FF1NPMU1UVV1KQ2. Построение сечения методом вспомогательного сечения (внутреннего
- 8. Комбинированный методСущность этого метода состоит в
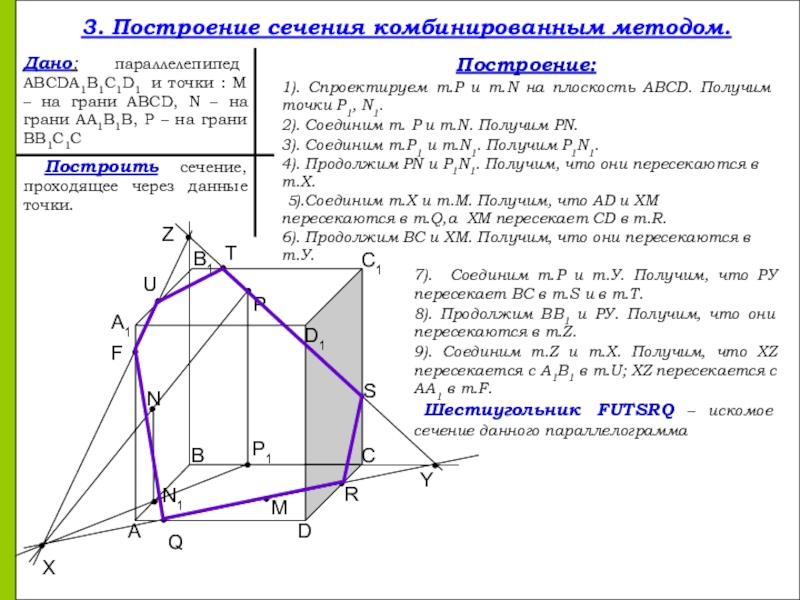
- 9. AA1BB1CC1DD1XNPYFUTZMN1QRSP13. Построение сечения комбинированным методом.Дано: параллелепипед ABCDA1B1C1D1
- 10. ВыводыПостроение сечений многогранников можно осуществлять на основании
Слайд 1Творческий проект по теме
«Методы построения сечений многогранников»
Выполнили:
Закирова Айгерим,
Шевляков Олег,
Жайсанбаев Сабыр.
Слайд 4
Слайд 5
A1
(Q’)
Q
R
P
C1
C2
C
D
D1
B
B1
R’
P’
S1
S2
S3
V
B2
1. Построение сечения методом следов.
Дано: четырёхугольная призма ABCDA1B1C1D1 и точки Р
Построить сечение, проходящее через данные точки.
Построение:
1). Проектируем точки P, Q, R. Они спроектируются на точки P’, Q’, R’.
2). Строим т.S1 – точка пересечения PR и P’R’ и т.S2 – точка пересечения QR и Q’R’.
3). Строим прямую S1S2 – линия пересечения плоскостей PQR и ABC.
4). Проведем прямую Q’D и найдем точку S3, в которой пересекаются прямые Q’D и S1S2.
5). Строим т.D2 – точка пересечения QS3 и DD1.
6). Проведем прямую D2C2 через т.Р.
7). Проведем С2R. Получим т.В2 – точка пересечения ВВ1 и С2R.
8). Проведем В2Q – линия пересечения ВВ1 и VQ. Получим т.V
9). Соединим т. V и т.R. Получим VR.
Многоугольник QD2C2R2V – искомое сечение.
D2
A
Слайд 6Метод внутреннего
проектирования
Сущность метода внутреннего проектирования заключается в нахождении по известным
Слайд 7
A
A1
B
B1
C
C1
D
D1
F
F1
N
P
M
U1
U
V
V1
K
Q
2. Построение сечения методом вспомогательного сечения (внутреннего проектирования).
Дано: призма ABCDFA1B1C1D1F1, точки
Построить сечение, проходящее через данные точки.
Построение:
1). Соединим т.P и т.N. Получим PN.
2). Соединим т.N и т.M. Получим NM.
3). Cсоединим т.P и т.М.
4). Спроектируем точки Р, N, M. Они спроектируются на точки С, D, F.
5). Соединим т.D и т.В. Получим, что DB и CF пересекаются в т.U1.
6). Спроектируем т.U1 на плоскость PNM. Получим т.U.
7). Спроектируем BD на плоскость PNM. Получим NQ.
8). Соединим т.D и т.A. Получим, что DA и CF пересекаются в т.V1.
9). Спроектируем т.V1 на плоскость PNM. Получим т.V.
10). Соединим т.V и т.N. Получим VN.
11). Спроектируем AD на плоскость PNM. Получим отрезок NK, который наложится на отрезок NV, т.е. NK является продолжением NV.
Пятиугольник KQPNM – искомое сечение данного куба.
Слайд 8
Комбинированный метод
Сущность этого метода состоит в том,
что на некоторых
сечения применяется метод следов
или метод внутреннего проецирования,
а на других этапах построения этого
сечения осуществляется с
использованием
теорем о параллельности в
пространстве и других.
Слайд 9
A
A1
B
B1
C
C1
D
D1
X
N
P
Y
F
U
T
Z
M
N1
Q
R
S
P1
3. Построение сечения комбинированным методом.
Дано: параллелепипед ABCDA1B1C1D1 и точки : М
Построить сечение, проходящее через данные точки.
Построение:
1). Спроектируем т.Р и т.N на плоскость ABCD. Получим точки P1, N1.
2). Соединим т. Р и т.N. Получим PN.
3). Соединим т.P1 и т.N1. Получим P1N1.
4). Продолжим PN и P1N1. Получим, что они пересекаются в т.X.
5).Соединим т.Х и т.М. Получим, что AD и XM пересекаются в т.Q,а ХМ пересекает CD в т.R.
6). Продолжим ВС и ХМ. Получим, что они пересекаются в т.У.
7). Соединим т.Р и т.У. Получим, что РУ пересекает ВС в т.S и в т.Т.
8). Продолжим ВВ1 и РУ. Получим, что они пересекаются в т.Z.
9). Соединим т.Z и т.Х. Получим, что XZ пересекается с А1B1 в т.U; XZ пересекается с AA1 в т.F.
Шестиугольник FUTSRQ – искомое сечение данного параллелограмма
Слайд 10Выводы
Построение сечений многогранников можно осуществлять на основании аксиом стереометрии и теорем
Сечения многогранников могут быть разными фигурами-многоугольниками, а так же точкой и отрезком.
Вместе с тем, существуют определенные методы построения плоских сечений многогранников. Наиболее эффективными являются следующие три метода:
- метод следов;
- метод внутреннего проецирования;
- комбинированный метод.