- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Теорема Пифагора
Содержание
- 1. Теорема Пифагора
- 2. Слайд 2
- 3. Свет истины рассеется не скоро, Но, воссияв,
- 4. Обычно открытие этого утверждения приписывают древнегреческому философу
- 5. ЦЕЛЬ ИССЛЕДОВАНИЯ.Узнать, кто такой был Пифагор и какое отношение он имеет к этой теореме.
- 6. Проблемные вопросы.1) Существуют ли другие доказательства этой
- 7. ХОД ИССЛЕДОВАНИЯ.Про жизнь Пифагора достоверно почти ничего
- 8. После одиннадцати лет обучения в Египте Пифагор
- 9. Пифагор организовал в греческой колонии на юге
- 10. ремы. Многим известен сонетВ настоящее время известно,
- 11. Древнекитайское доказательство.На древнекитайском чертеже четыре равных прямоугольных
- 12. Доказательство простейшее. Это доказательство получается в простейшем случае
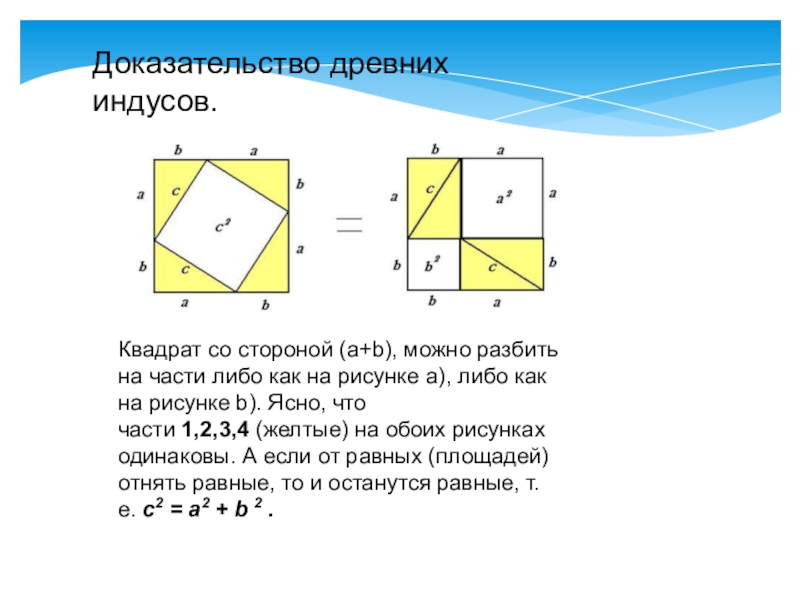
- 13. Доказательство древних индусов. Квадрат со стороной (a+b),
- 14. Применение теоремы Пифагора.Применение теоремы ПифагораЗадачи практические старинные.Для
- 15. На берегу реки рос тополь одинокий.Вдруг ветра
- 16. 800 м600 м Мальчик прошёл от дома по
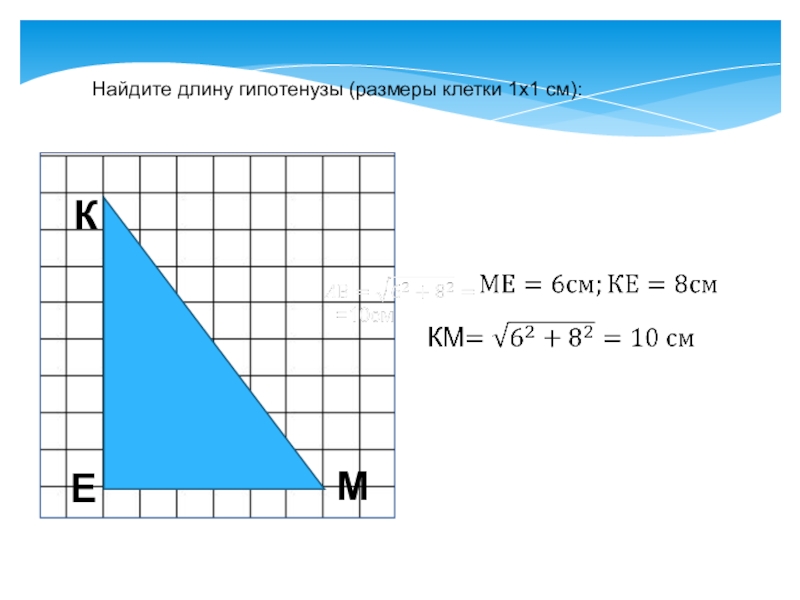
- 17. Найдите длину гипотенузы (размеры клетки 1х1 см): КЕМ
- 18. Теорема Пифагора настолько известна, что трудно представить
- 19. ЛИТЕРАТУРА1. Учебник “Геометрия 7–9” , Л.С. Атанасян2.
Слайд 1
Теорема Пифагора.
Работу выполнила
ученица 8-го класса А
Милосердова Т.В.
Слайд 2
В этом учебном году мы познакомились с интересной теоремой, известной, как оказалось с древнейших времён:
«Квадрат, построенный на гипотенузе прямоугольного треугольника равновелик сумме квадратов построенных на катетах».
Слайд 3Свет истины рассеется не скоро, Но, воссияв, рассеется навряд И, как тысячелетия назад, Не
Адельберт фон Шамиссо.
Слайд 4Обычно открытие этого утверждения приписывают древнегреческому философу и математику Пифагору (VI
П
Слайд 6
Проблемные вопросы.
1) Существуют ли другие доказательства этой теоремы?
2) Каково значение этой
3) Какую роль сыграл Пифагор в развитии математики?
4) Какие задачи можно решить с помощью этой теоремы?
Слайд 7ХОД ИССЛЕДОВАНИЯ.
Про жизнь Пифагора достоверно почти ничего не известно, но с
Пифагор родился в 570 году до н. э на острове Самос. Отцом Пифагора был Мнесарх – резчик по драгоценным камням. Мнесарх, по словам Апулея, «славился среди мастеров своим искусством вырезать геммы», но стяжал скорее славу, чем богатство. Имя матери Пифагора не сохранилось.
Пифагор имел красивую внешность, носил длинную бороду, а на голове золотую диадему. Пифагор - это не имя, а прозвище, которое философ получил за то, что всегда говорил верно и убедительно, как греческий оракул. (Пифагор - "убеждающий речью".) В 550 году до н. э Пифагор принимает решение и отправляется в Египет. Итак, перед Пифагором открывается неизвестная страна и неведомая культура. Многое поражало и удивляло Пифагора в этой стране, и после некоторых наблюдений за жизнью египтян Пифагор понял, что путь к знаниям, охраняемым кастой жрецов, лежит через религию.
Слайд 8После одиннадцати лет обучения в Египте Пифагор отправляется на родину, где
Именно в Кротоне начинается самый славный период в жизни Пифагора.
Слайд 9
Пифагор организовал в греческой колонии на юге Апенинского полуострова религиозно-этическое братство,
Система морально-этических правил, завещанная Пифагором своим ученикам, была собрана в своеобразный моральный кодекс пифагорейцев «Золотые
стихи», которые пользовались большой популярностью в эпоху Античности, эпоху Средневековья и эпоху Возрождения. Пифагорейская система занятий состояла из трёх разделов:
· учения о числах – арифметике,
· учения о фигурах – геометрии,
· учения о строении Вселенной – астрономии.
Система образования, заложенная Пифагором, просуществовала много веков.
Слайд 10ремы. Многим известен сонет
В настоящее время известно, что эта теорема не
Как мы видим, история математики почти не сохранила достоверных конкретных данных о жизни Пифагора и его математической деятельности, но легенды говорят, что именно Пифагор дал полноценное научное доказательство этой теоремы. Рассмотрим различные доказательства этой теоремы.з
Слайд 11Древнекитайское доказательство.
На древнекитайском чертеже четыре равных прямоугольных треугольника с катетами a , b и гипотенузой с
a2 + 2ab +b2 = c2 + 2ab
a2 +b2 = c2
Слайд 12Доказательство простейшее.
Это доказательство получается в простейшем случае равнобедренного прямоугольного треугольника.
Вероятно, с
В самом деле, достаточно просто посмотреть на мозаику равнобедренных прямоугольных треугольников, чтобы убедиться в справедливости теоремы.
Например, для треугольника АВС: квадрат, построенный на гипотенузе АС, содержит 4 исходных треугольника, а квадраты, построенные на катетах, - по два. Теорема доказана.
Слайд 13
Доказательство древних индусов.
Квадрат со стороной (a+b), можно разбить на части
Слайд 14
Применение теоремы Пифагора.
Применение теоремы Пифагора
Задачи практические старинные.
Для крепления мачты нужно установить
4
Случися некому человеку к стене лестницу прибрати, стены же тоя высота есть 117 стоп. И обреете лестницу долготью 125 стоп.
И ведати хочет, колико стоп сея лестницы нижний конец от стены отстояти имать."
Слайд 15На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Задача индийского математика XII века Бхаскары .
Слайд 16
800 м
600 м
Мальчик прошёл от дома по направлению на восток 800
Современные задачи.
Слайд 18
Теорема Пифагора настолько известна, что трудно представить себе человека, не слышавшего
Теорема Пифагора - одна из главных и, можно сказать, самая главная теорема геометрии. Значение ее состоит в том, что из нее или с ее помощью можно вывести большинство теорем геометрии.
Заслуга же Пифагора состояла в том, что он дал полноценное научное доказательство этой теоремы.
Интересна личность самого учёного, память о котором неслучайно сохранила эта теорема. Пифагор – замечательный оратор, учитель и воспитатель, организатор своей школы, ориентированной на гармонию музыки и чисел, добра и справедливости, на знания и здоровый образ жизни. Он вполне может служить примером для нас, далёких потомков.
Результаты исследования.
Слайд 19ЛИТЕРАТУРА
1. Учебник “Геометрия 7–9” , Л.С. Атанасян
2. .Войтикова Н.В. «Теорема Пифагора»
3. В. Литцман .Теорема Пифагора, М. 1960.
4. А.В. Волошинов «Пифагор» М. 1993.
5. Л. Ф. Пичурин «За страницами учебника алгебры» М. 1990.
6. http://ru.wikipedia.org/wiki/Теорема_Пифагора
7. http://th-pif.narod.ru/history.htm