- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Тема : Разные способы доказательства теоремы Пифагора
Содержание
- 1. Тема : Разные способы доказательства теоремы Пифагора
- 2. Теорема Пифагора и способы ее доказательстваСодержание:ВведениеИстория открытия
- 3. Слайд 3
- 4. Слайд 4
- 5. Слайд 5
- 6. Доказательство теоремы Пифагора по косинусуПостроим из прямого
- 7. Опустим высоту на гипотенузу C .Площадь треугольника-S
- 8. ВЕКТОРНОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫПусть АВС - прямоугольный треугольник
- 9. Доказательство теоремы Пифагора по БасхариЭто прямоугольный треугольникИллюстрирует
- 10. Доказательство теоремы Пифагора методом Гофмана и МёльманнаМетод
- 11. Доказательство теоремы Пифагора методом
- 12. Наиболее привычный способ доказательства теоремы Пифагора.Это равнобедренный
- 13. ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО МЕТОДОМ ГАРФИЛДА Дано: ABC-прямоугольный треугольникДоказать:
- 14. ДОКАЗАТЕЛЬСТВА МЕТОДОМ ДОСТРОЕНИЯСущность этого метода состоит в
- 15. На рисунке Пифагорова фигура достроена до
- 16. Теперь докажем, что фигуры, вычитаемые в первом
- 17. Рис. 11 иллюстрирует еще одно более оригинальное доказательство,
- 18. Доказательство теоремы Пифагора по ЕвклидуAJ- высота, опущенная
- 19. S треугольника ABD=1/2 Sпрямоугольника BJLD, т.к. у
- 20. ПИФАГОРОВЫ ТРОЙКИПифагоровы тройки – это наборы из трёх
- 21. ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРАТеорема Пифагора издавна применялась в
- 22. ЗАКЛЮЧЕНИЕВ заключении еще раз хочется сказать о
- 23. СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ1. Атанасян Л.С., Бутузов Б.Л.,
Слайд 1МУНИЦИПАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ЛАГОЛОВСКАЯ ОСНОВНАЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА
СЕКЦИЯ: МАТЕМАТИКА
Тема : «Разные
теоремы Пифагора»
Участники проекта:
1.Беляков Андрей-ученик 9 класса
2.Алексеева Наталья-ученица 9 класса
Руководитель проекта:
Кондратьева Л.А.-учитель математики
д. Лаголово
Ломоносовский район
2014 год
Слайд 2Теорема Пифагора и способы ее доказательства
Содержание:
Введение
История открытия теоремы Пифагора
Биография Пифагора
Доказательство теоремы
Доказательство теоремы Пифагора по площади
Векторное доказательство теоремы Пифагора
Доказательство теоремы Пифагора по Басхари
Доказательство теоремы Пифагора методом Гофмана и Мёльманна
Наиболее привычный способ доказательства теоремы Пифагора
Геометрическое доказательство методом Гарфилда
Доказательство теоремы Пифагора методом достроения
Доказательство теоремы Пифагора по Евклиду
Пифагоровы тройки
Применение теоремы Пифагора
Заключение
Список использованной литературы
Слайд 3
Слайд 4
Слайд 5
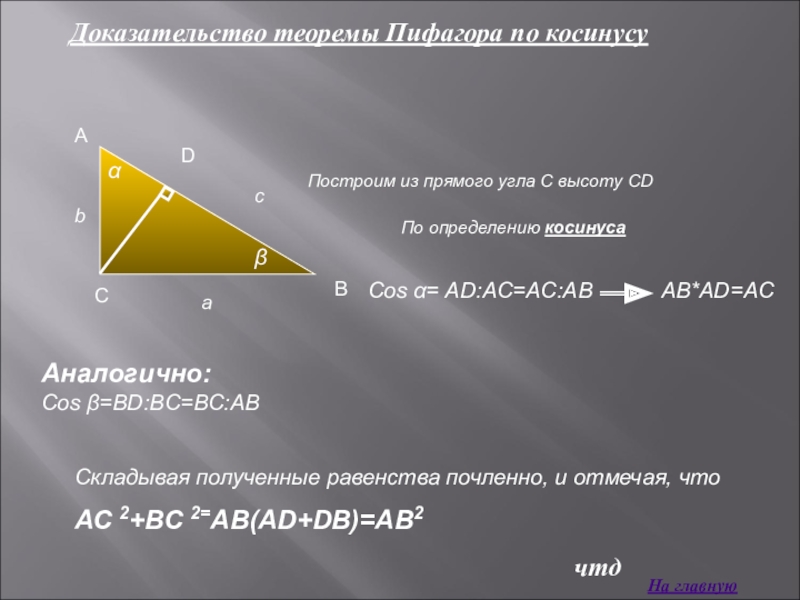
Слайд 6Доказательство теоремы Пифагора по косинусу
Построим из прямого угла С высоту СD
По
Аналогично:
Cos β=BD:BC=BC:AB
Складывая полученные равенства почленно, и отмечая, что
АС 2+BС 2=AB(AD+DB)=AB2
чтд
На главную
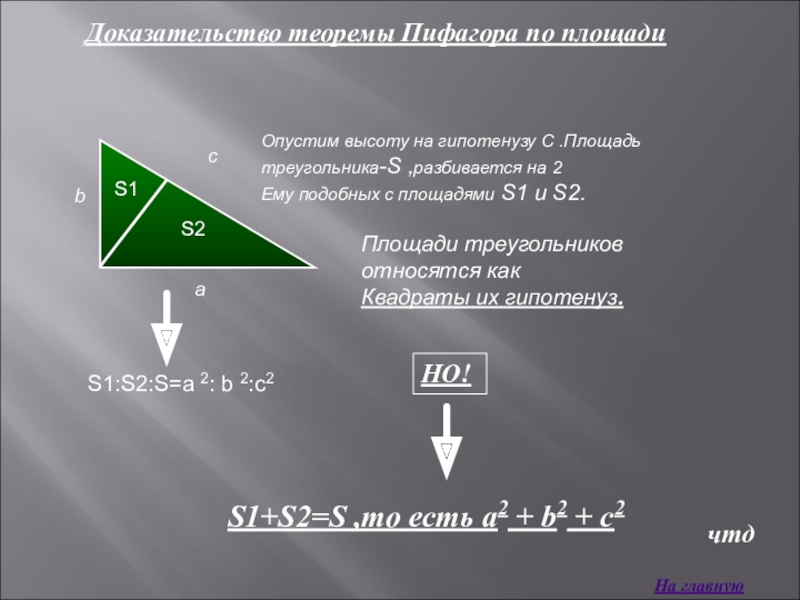
Слайд 7Опустим высоту на гипотенузу C .Площадь треугольника-S ,разбивается на 2
Ему подобных
Площади треугольников относятся как
Квадраты их гипотенуз.
Доказательство теоремы Пифагора по площади
НО!
чтд
На главную
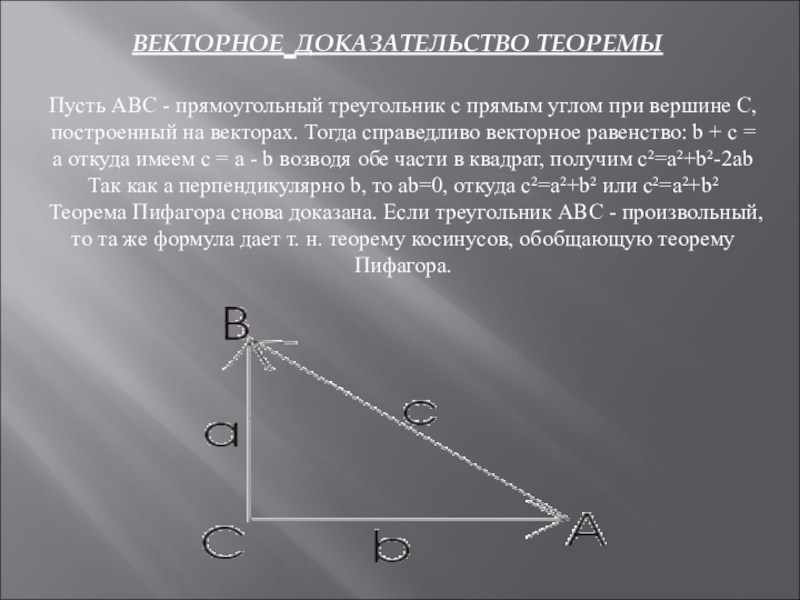
Слайд 8ВЕКТОРНОЕ ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ
Пусть АВС - прямоугольный треугольник с прямым углом при
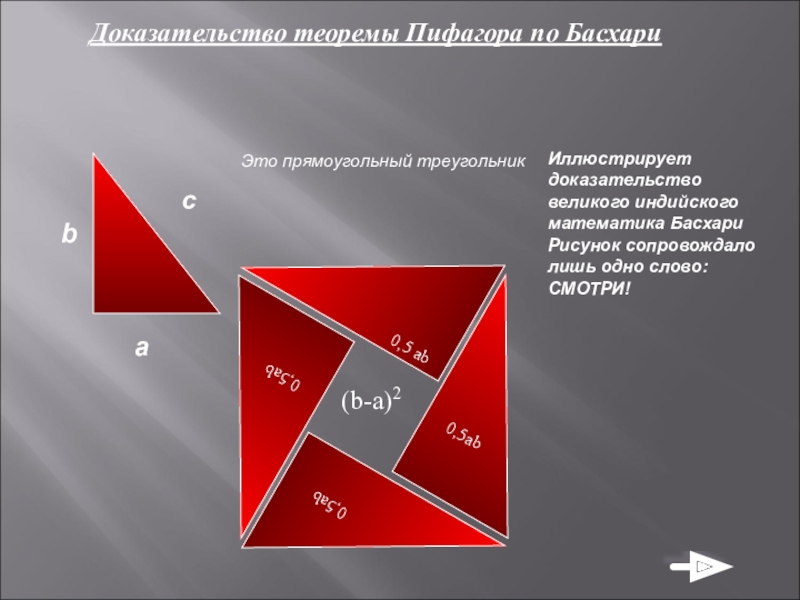
Слайд 9Доказательство теоремы Пифагора по Басхари
Это прямоугольный треугольник
Иллюстрирует доказательство великого индийского математика
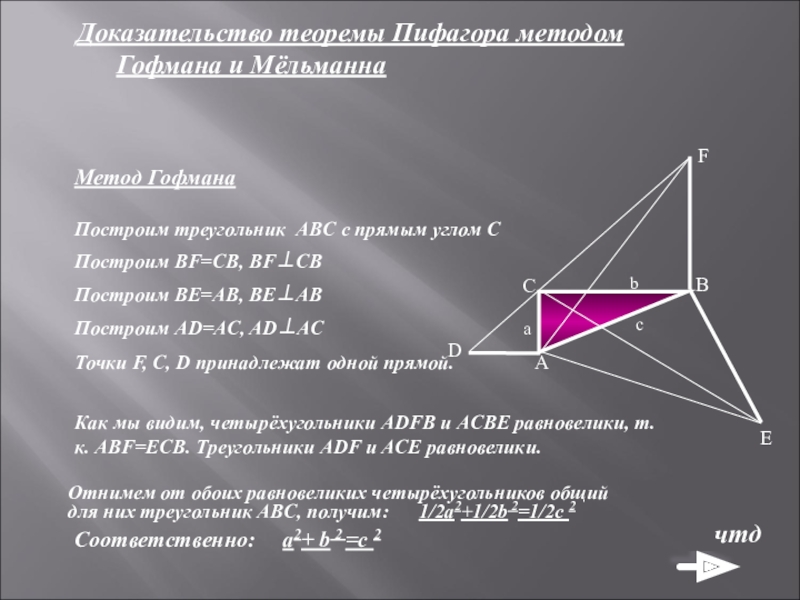
Слайд 10Доказательство теоремы Пифагора методом Гофмана и Мёльманна
Метод Гофмана
Построим треугольник ABC с
Построим BF=CB, BF⊥CB
Построим BE=AB, BE⊥AB
Построим AD=AC, AD⊥AC
Точки F, C, D принадлежат одной прямой.
Как мы видим, четырёхугольники ADFB и ACBE равновелики, т.к. ABF=ЕCB. Треугольники ADF и ACE равновелики.
Отнимем от обоих равновеликих четырёхугольников общий для них треугольник ABC, получим: 1/2а2+1/2b 2=1/2с 2
чтд
Соответственно: а2+ b 2 =с 2
Слайд 11Доказательство теоремы Пифагора методом Гофмана и Мёльманна
Метод
Площадь данного прямоугольника с одной стороны равна 0.5ab, с другой 0.5pr, где p – полупериметр треугольника, r – радиус вписанной в него окружности (r = 0.5(a+b-c)).
Имеем:
0.5ab=0.5pr=0.5(a+b+c)*0.5(a+b-c)
Отсюда следует , что
с2=а2+b2
чтд
На главную
Слайд 12
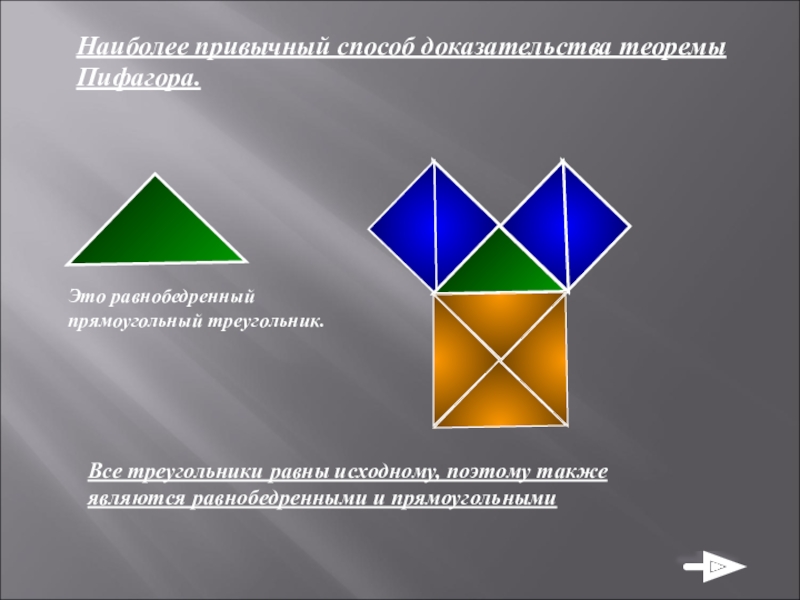
Наиболее привычный способ доказательства теоремы Пифагора.
Это равнобедренный прямоугольный треугольник.
Все треугольники
Слайд 13ГЕОМЕТРИЧЕСКОЕ ДОКАЗАТЕЛЬСТВО
МЕТОДОМ ГАРФИЛДА
Дано: ABC-прямоугольный треугольник
Доказать: BC²=AB²+AC²
Доказательство:
1) Построим отрезок CD равный
2) Площадь фигуры ABED можно найти, если рассматривать её как сумму площадей трёх треугольников: SABED=2×AB×AC/2+BC²/2
3) Фигура ABED является трапецией, значит, её площадь равна:
S ABED=((DE+AB)/2)×AD
4) Если приравнять левые части найденных выражений, то получим:
AB×AC+BC²/2=(DE+AB)(CD+AC)/2
AB×AC+BC²/2= (AC+AB)²/2
AB×AC+BC²/2= AC²/2+AB²/2+AB×AC
BC²=AB²+AC².
Слайд 14ДОКАЗАТЕЛЬСТВА МЕТОДОМ ДОСТРОЕНИЯ
Сущность этого метода состоит в том, что к квадратам,
На рисунке изображена обычная Пифагорова фигура – прямоугольный треугольник ABC
с построенными на его сторонах квадратами. К этой фигуре присоединены треугольники 1 и 2, равные исходному прямоугольному треугольнику.
Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ. Здесь CОEP, прямая EP делит шестиугольник AEDFPB на два равновеликих четырехугольника, прямая CM делит шестиугольник ACBNMQ на два равновеликих четырехугольника; поворот плоскости на 90° вокруг центра A отображает четырехугольник AEPB на четырехугольник ACMQ.
Слайд 15 На рисунке Пифагорова фигура достроена до прямоугольника, стороны которого параллельны
Слайд 16Теперь докажем, что фигуры, вычитаемые в первом случае, равновелики фигурам, вычитаемым
Рисунок иллюстрирует доказательство, приведенное Нассир-эд-Дином (1594 г.). Здесь: PCL – прямая;
KLOA = ACPF = ACED = a2;
LGBO = CBMP = CBNQ = b2;
AKGB = AKLO + LGBO = c2; отсюда c2 = a2 + b2.
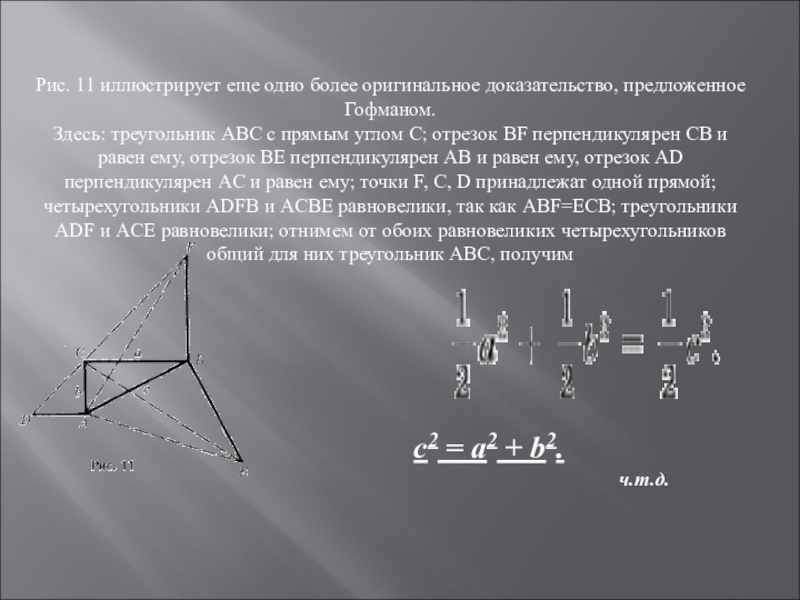
Слайд 17Рис. 11 иллюстрирует еще одно более оригинальное доказательство, предложенное Гофманом. Здесь: треугольник ABC
c2 = a2 + b2.
ч.т.д.
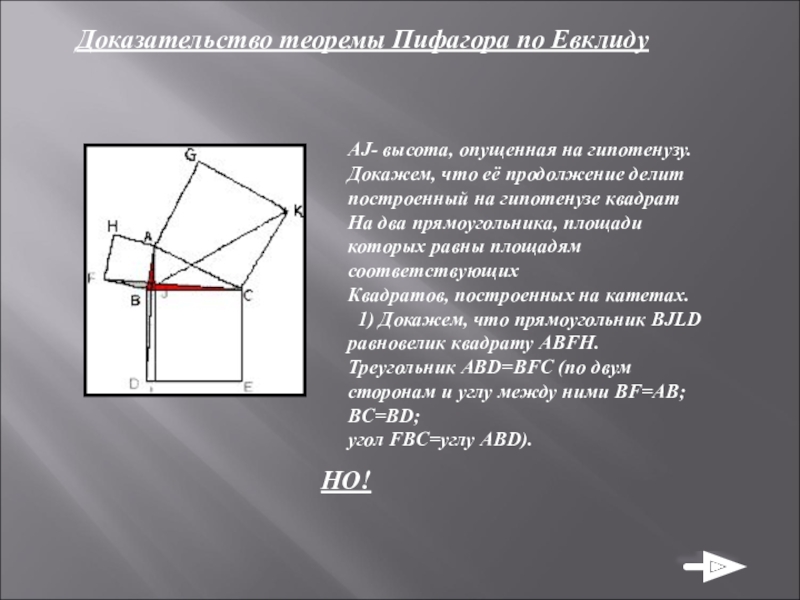
Слайд 18Доказательство теоремы Пифагора по Евклиду
AJ- высота, опущенная на гипотенузу.
Докажем, что её
На два прямоугольника, площади которых равны площадям соответствующих
Квадратов, построенных на катетах.
1) Докажем, что прямоугольник BJLD равновелик квадрату ABFH.
Треугольник ABD=BFC (по двум сторонам и углу между ними BF=AB; BC=BD;
угол FBC=углу ABD).
НО!
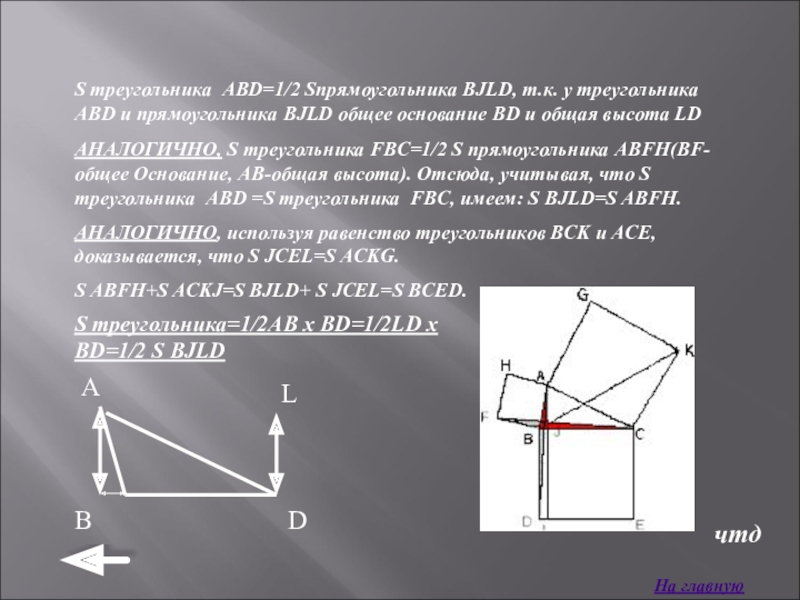
Слайд 19S треугольника ABD=1/2 Sпрямоугольника BJLD, т.к. у треугольника ABD и прямоугольника
АНАЛОГИЧНО, S треугольника FBC=1/2 S прямоугольника ABFH(BF-общее Основание, AB-общая высота). Отсюда, учитывая, что S треугольника ABD =S треугольника FBC, имеем: S BJLD=S ABFH.
АНАЛОГИЧНО, используя равенство треугольников BCK и ACE, доказывается, что S JCEL=S ACKG.
S ABFH+S ACKJ=S BJLD+ S JCEL=S BCED.
S треугольника=1/2AB x BD=1/2LD x BD=1/2 S BJLD
чтд
На главную
Слайд 20ПИФАГОРОВЫ ТРОЙКИ
Пифагоровы тройки – это наборы из трёх натуральных чисел (x, y
Некоторые Пифагоровы тройки: (3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17), (12, 16, 20), (15, 20, 25), (7, 24, 25), (10, 24, 26), (20, 21, 29), (18, 24, 30), (10, 30, 34), (21, 28, 35), (12, 35, 37), (15, 36, 39), (24, 32, 40), (9, 40, 41), (27, 35, 45), (14, 48, 50), (30, 40, 50)… Пифагоровы тройки имеют важное значение в геометрии. Несмотря на то, что в школе на изучение Пифагоровых троек не отводится много времени, в настоящее время знание их необходимо при решении многих математических задач.
Слайд 21ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА
Теорема Пифагора издавна применялась в разных областях науки и
Слайд 22ЗАКЛЮЧЕНИЕ
В заключении еще раз хочется сказать о важности теоремы. В наши
Слайд 23СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
1. Атанасян Л.С., Бутузов Б.Л., Кадомцев С.Б. и др.
2. Глейзер Г., Учебно-методическая газета Математика, №4 2005г.
3. Киселёв А.П. , Геометрия. Часть первая. Планиметрия, Москва,Просвещение,1969г. 4. Остренкова Г., Учебно-методическая газета Математика, №24 2001г. 5. Семёнов Е.Е. «Изучаем геометрию», Москва, Просвещение ,1987г. 6. Скопец З.А. «Геометрические миниатюры» , Москва, Просвещение,1990г. 7. Ткачева М.В. Домашняя математика , Москва, Просвещение ,1994г.
8. Интернет-источники: http://bankreferatov.ru/ http://kvant.ru/ http://th-pif.narod.ru/formul.html