- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Смежные и вертикальные углы.
Содержание
- 1. Смежные и вертикальные углы.
- 2. Давай вспомним!Что такое угол?
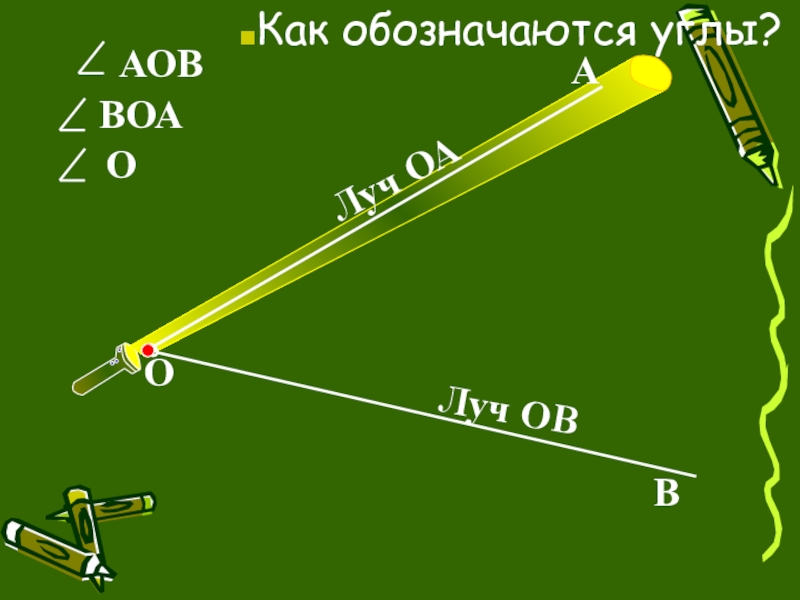
- 3. АОВОВВОААОЛуч ОАЛуч ОВКак обозначаются углы?
- 4. Для измерения углов используют транспортир .Какой инструмент можно использовать для измерения углов?
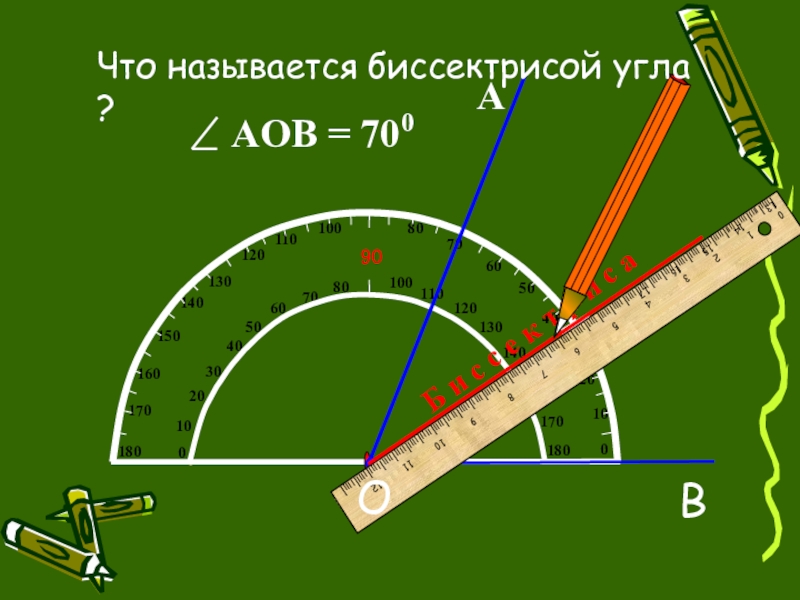
- 5. АБ и с с е к т р и с а Что называется биссектрисой угла ?BO
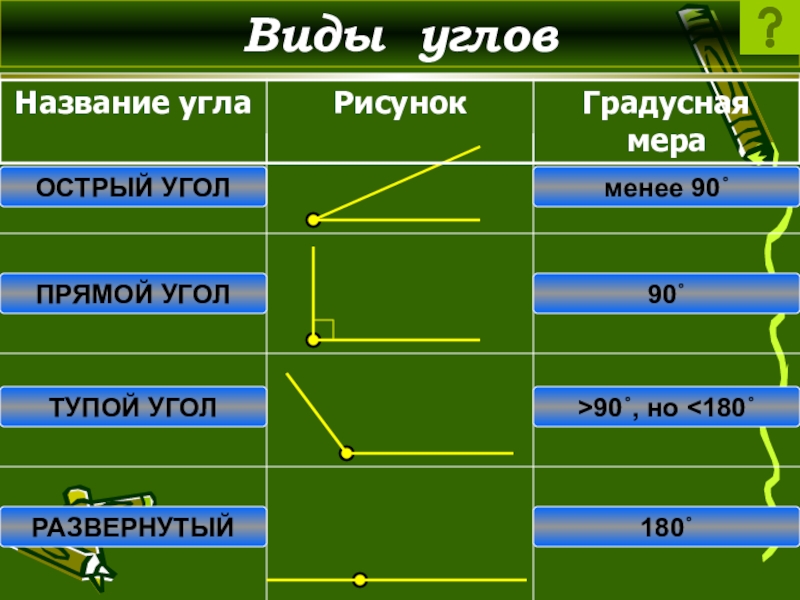
- 6. Виды угловОСТРЫЙ УГОЛПРЯМОЙ УГОЛТУПОЙ УГОЛРАЗВЕРНУТЫЙменее 90˚90˚>90˚, но
- 7. Какой угол образует клюв вороны, когда: "Ворона
- 8. К вашим знаниям об углах сегодня добавится еще два вида: Смежные и вертикальные углы.
- 9. ПланОпределение смежных угловПостроение смежных угловСвойство смежных угловПример
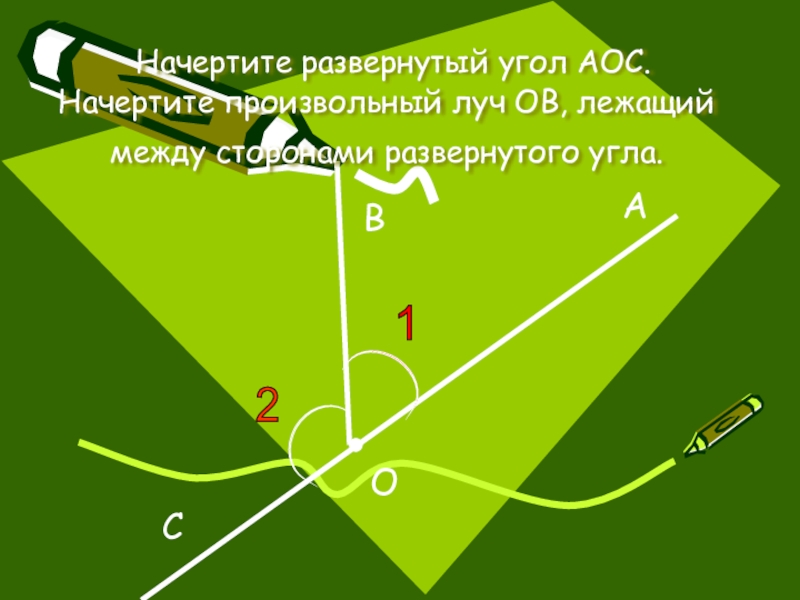
- 10. 1 ABCO Начертите развернутый угол АОС. Начертите произвольный луч ОB, лежащий между сторонами развернутого угла.
- 11. Определение смежных угловОпределение. Два угла называются смежными,
- 12. Построение смежных углов
- 13. АОВ С Угол
- 14. 1. Одну из сторон угла продолжить за
- 15. Одну из сторон угла продолжить за его
- 16. Cвойство смежных углов1. Сколько углов изображено на
- 17. Теорема. Сумма смежных углов равна
- 18. Решение:
- 19. Пример оформления решения задачиОдин из смежных углов
- 20. Начертите произвольный ∠AOB. Постройте лучи OC и
- 21. CDПостроить угол.2.Продлить каждую сторону угла за его вершину.
- 22. Теорема. Вертикальные углы равны.Дано: ∠AOD и ∠COB
- 23. Образец оформления решения задачиПри пересечении двух прямых
- 24. Обучающая самостоятельная работа2. Начертите угол МОК. Постройте
- 25. 12назадПорешаем?
- 26. Задания для самопроверки13Задача 2. Один из четырех
- 27. Козьма ПрутковОтыщи сему начало, и ты многое поймешь 16
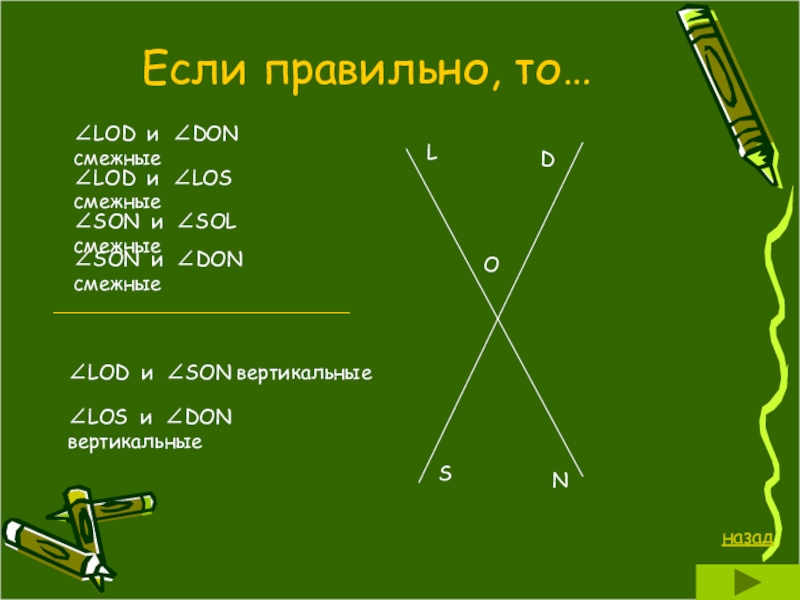
- 28. Если правильно, то…
Слайд 4Для измерения углов используют транспортир .
Какой инструмент можно использовать для измерения
Слайд 7Какой угол образует клюв вороны, когда: "Ворона сыр во рту держала?"
А когда "Ворона каркнула во все воронье горло?"
Слайд 9План
Определение смежных углов
Построение смежных углов
Свойство смежных углов
Пример оформления задачи
Вертикальные углы
Свойство вертикальных
Построение вертикальных углов
Пример оформления задачи
Приложения
Домашнее задание
2
Слайд 10
1
A
B
C
O
Начертите развернутый угол АОС. Начертите произвольный луч ОB, лежащий
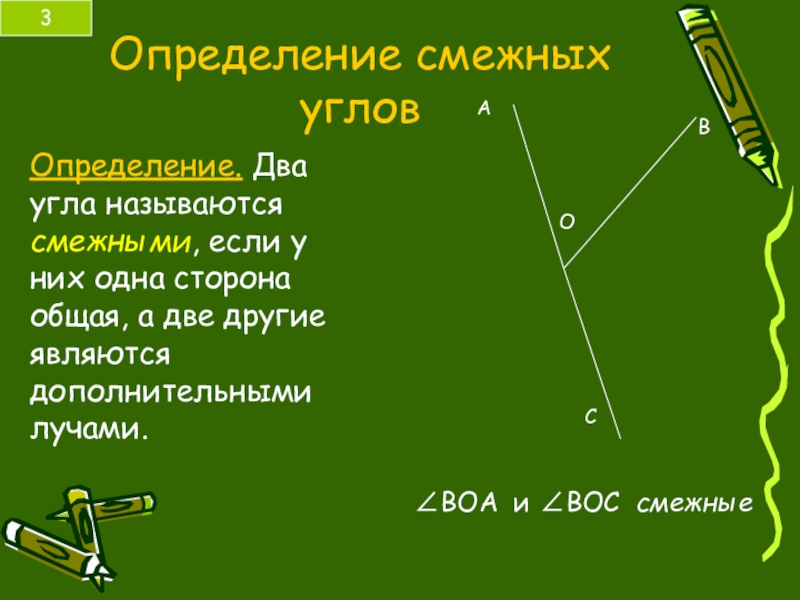
Слайд 11Определение смежных углов
Определение. Два угла называются смежными, если у них одна
3
∠ВОА и ∠ВОС смежные
Слайд 13А
О
В
С
Угол смежный для острого
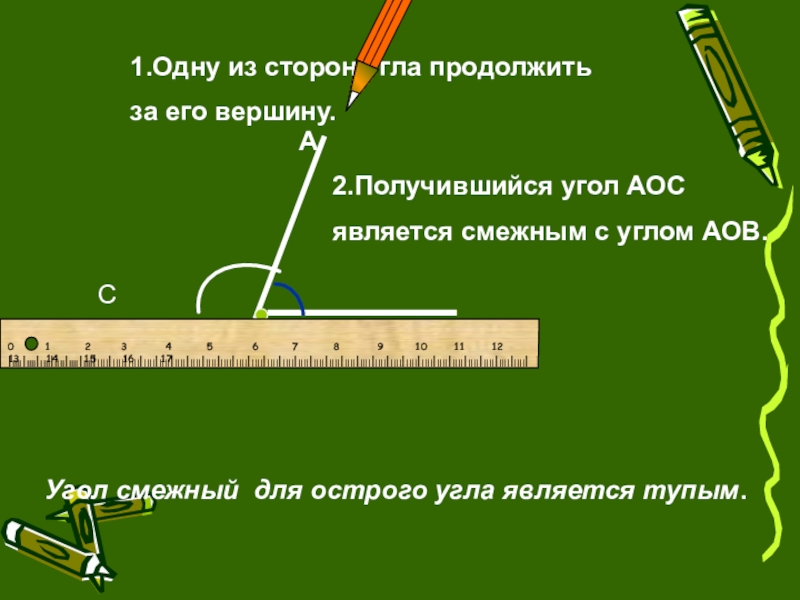
1.Одну из сторон угла продолжить
за его вершину.
2.Получившийся угол АОС
является смежным с углом АОВ.
Слайд 141. Одну из сторон угла продолжить за его вершину.
2. Получившийся угол
А
В
С
О
Угол смежный для тупого угла является острым.
Слайд 15
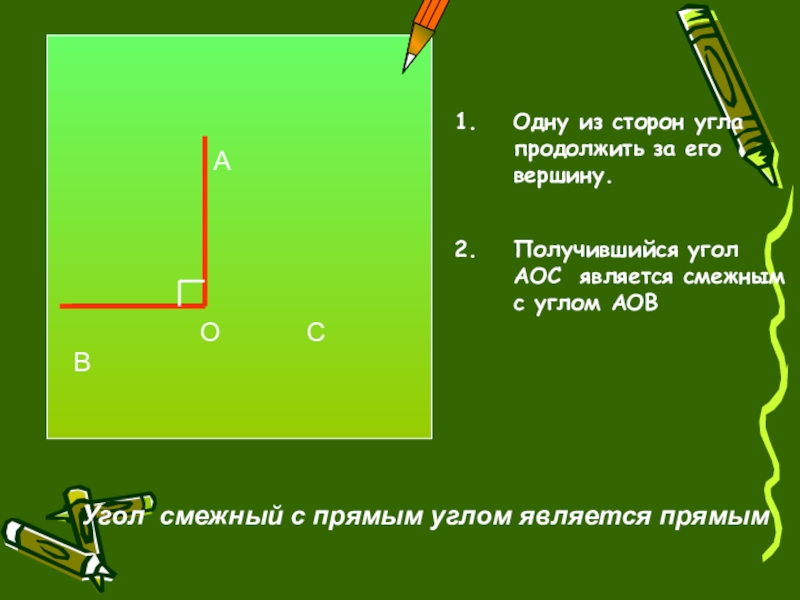
Одну из сторон угла продолжить за его вершину.
Получившийся угол АОС
А
В
О
С
Угол смежный с прямым углом является прямым
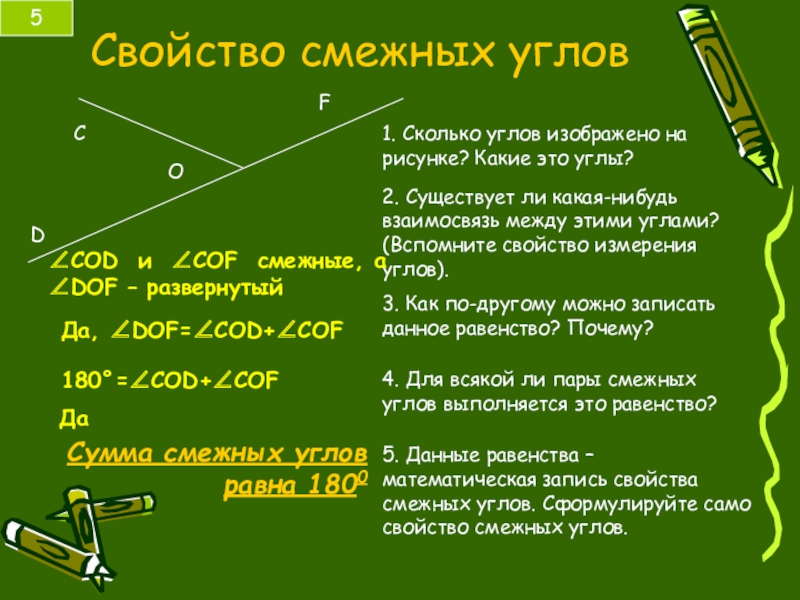
Слайд 16Cвойство смежных углов
1. Сколько углов изображено на рисунке? Какие это углы?
2.
3. Как по-другому можно записать данное равенство? Почему?
4. Для всякой ли пары смежных углов выполняется это равенство?
5. Данные равенства – математическая запись свойства смежных углов. Сформулируйте само свойство смежных углов.
Да
Сумма смежных углов равна 1800
5
∠СOD и ∠COF смежные, а
∠DOF – развернутый
Да, ∠DOF=∠COD+∠COF
180°=∠СOD+∠COF
Слайд 17
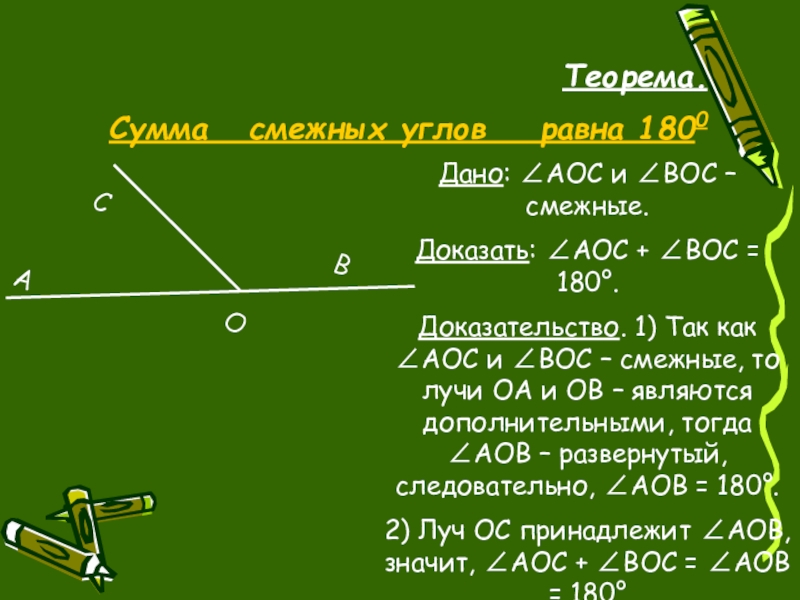
Теорема.
Сумма смежных углов равна 1800
Дано: ∠AOC и ∠BOC
Доказать: ∠AOC + ∠BOC = 180°.
Доказательство. 1) Так как ∠AOC и ∠BOC – смежные, то лучи ОА и ОВ – являются дополнительными, тогда ∠AOB – развернутый, следовательно, ∠AOB = 180°.
2) Луч OC принадлежит ∠AOB, значит, ∠AOC + ∠BOC = ∠AOB = 180°
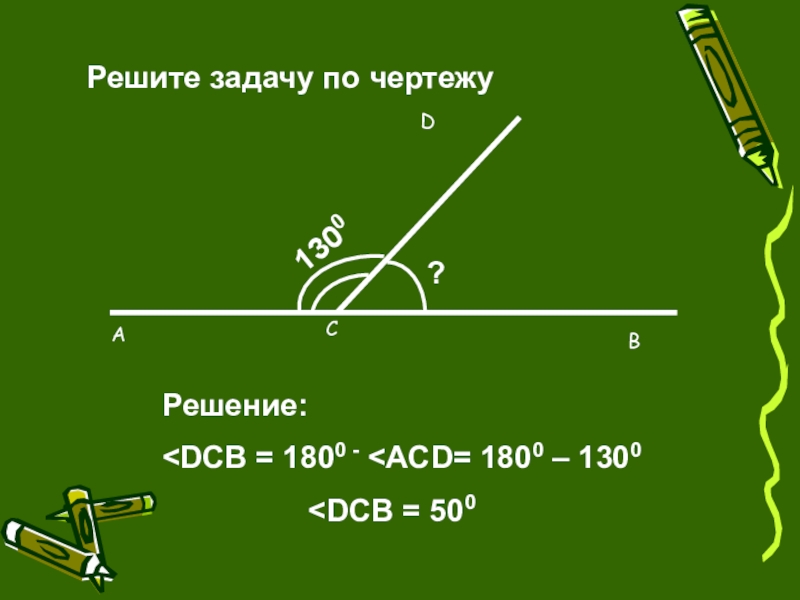
Слайд 19Пример оформления решения задачи
Один из смежных углов на 320 больше другого.
Решение:
6
Ответ: 740, 1060
∠KOM и ∠KON смежные,
∠KOM - ∠KON = 32°.
Дано:
Найти:
∠KOM , ∠KON .
Пусть ∠КОN = x, тогда ∠КОM = x+32°.
По свойству смежных углов: ∠KOM + ∠KON = 180°.
Значит, х +32°+х =180°,
2х = 180°- 32°,
2х = 148°,
х = 148°:2,
х = 74°.
∠КОN = 74°, тогда ∠КОM = 74° +32°=106°.
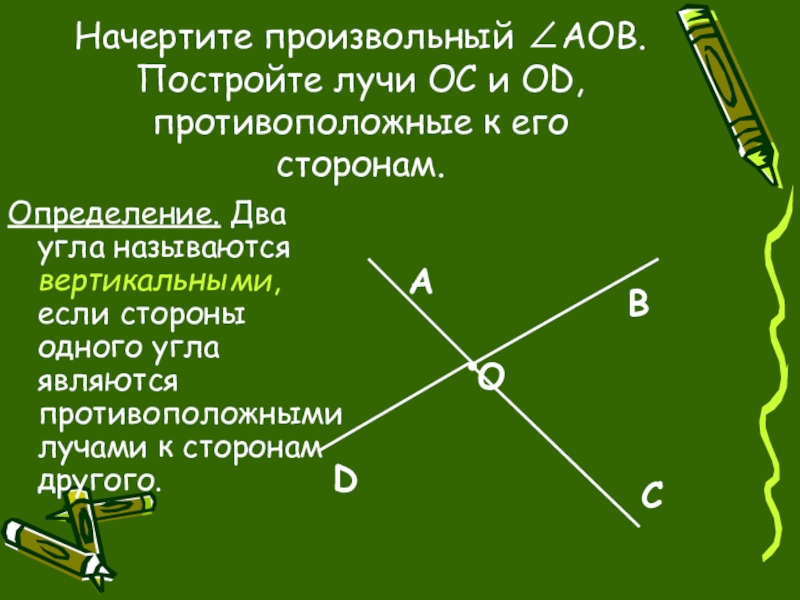
Слайд 20Начертите произвольный ∠AOB. Постройте лучи OC и OD, противоположные к его
В
С
D
Определение. Два угла называются вертикальными, если стороны одного угла являются противоположными лучами к сторонам другого.
Слайд 22
Теорема. Вертикальные углы равны.
Дано: ∠AOD и ∠COB – вертикальные.
Доказать: ∠AOD=∠COB
Доказательство. Каждый
и ∠COВ + ∠AOB = 180°. Имеем: ∠AOD = 180° – ∠AOB и ∠COB = 180° – ∠AOB, значит, ∠AOD = ∠COB
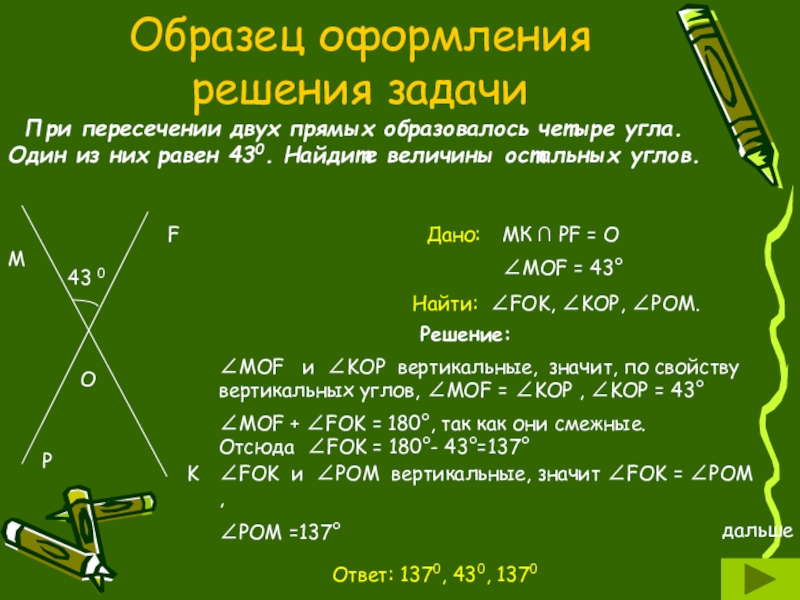
Слайд 23Образец оформления решения задачи
При пересечении двух прямых образовалось четыре угла. Один
Дано:
Найти:
Решение:
Ответ: 1370, 430, 1370
МК ∩ PF = О
∠МОF = 43°
∠FOK, ∠KOP, ∠POM.
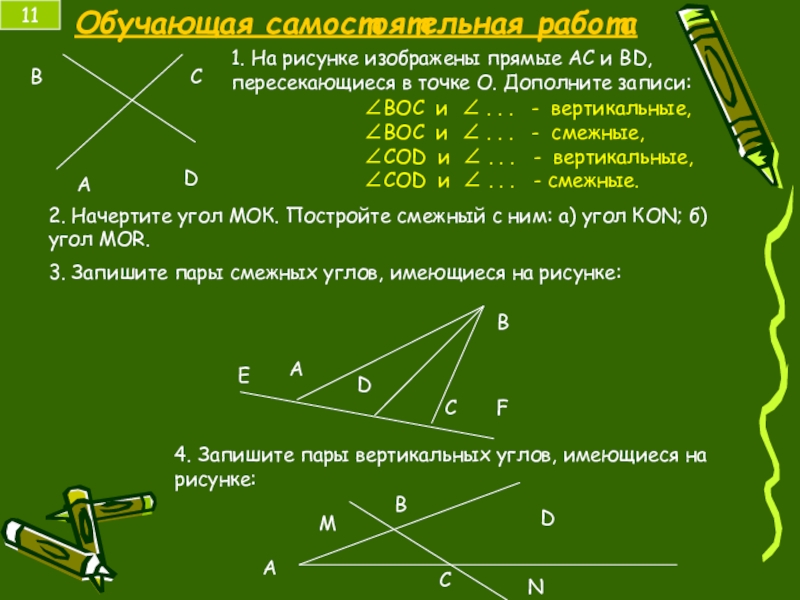
Слайд 24Обучающая самостоятельная работа
2. Начертите угол МОК. Постройте смежный с ним: а)
3. Запишите пары смежных углов, имеющиеся на рисунке:
4. Запишите пары вертикальных углов, имеющиеся на рисунке:
11
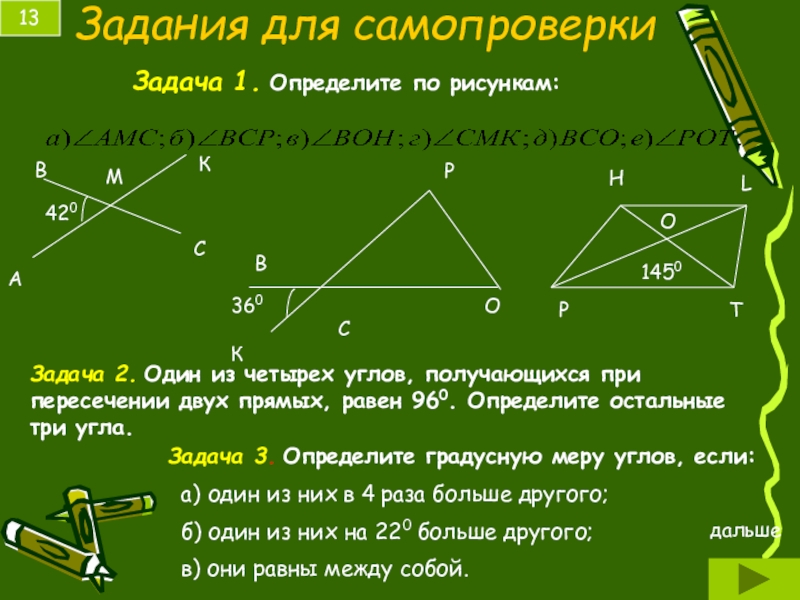
Слайд 26Задания для самопроверки
13
Задача 2. Один из четырех углов, получающихся при пересечении
Задача 3. Определите градусную меру углов, если:
а) один из них в 4 раза больше другого;
б) один из них на 220 больше другого;
в) они равны между собой.