- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Работы учащихся. Информационная презентация по теме: Золотое сечение ученицы 9 класса
Содержание
- 1. Работы учащихся. Информационная презентация по теме: Золотое сечение ученицы 9 класса
- 2. Золотое
- 3. Практическое знакомство с золотым сечением начинают с
- 4. Другой пример золотого сечения был обнаружен в
- 5. У нас есть прямоугольник: обозначим его буквой
- 6. Допустим возьмём пример из жизни:
- 7. Первый способ — по данной стороне S с
- 8. Третий способ. В данный круг вписать правильный пятиугольник.
- 9. СПАСИБО ЗА ВНИМАНИЕ
- 10. Золотое сечениеПодготовила Шабанова Ксения, ученица 8 В класса
Золотое сечение – это такое пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами,
Слайд 2 Золотое сечение – это такое
пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или другими словами, меньший отрезок так относится к большему, как больший ко всему
a : b= b : c или с : b= b : а.
Рис. 1.Геометрическое изображение золотой пропорции
a : b= b : c или с : b= b : а.
Рис. 1.Геометрическое изображение золотой пропорции
Слайд 3Практическое знакомство с золотым сечением начинают с деления
отрезка прямой в
золотой пропорции с помощью циркуля и линейки.
Рис. 2. Деление отрезка прямой по золотому сечению.
BC= 1/2 AB; CD= BC
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции. Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE= 0,618..., если АВ принять за единицу, ВЕ= 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям. Свойства золотого сечения описываются уравнением:
x2 – x – 1= 0
Рис. 2. Деление отрезка прямой по золотому сечению.
BC= 1/2 AB; CD= BC
Из точки В восставляется перпендикуляр, равный половине АВ. Полученная точка С соединяется линией с точкой А. На полученной линии откладывается отрезок ВС, заканчивающийся точкой D. Отрезок AD переносится на прямую АВ. Полученная при этом точка Е делит отрезок АВ в соотношении золотой пропорции. Отрезки золотой пропорции выражаются бесконечной иррациональной дробью AE= 0,618..., если АВ принять за единицу, ВЕ= 0,382... Для практических целей часто используют приближенные значения 0,62 и 0,38. Если отрезок АВ принять за 100 частей, то большая часть отрезка равна 62, а меньшая – 38 частям. Свойства золотого сечения описываются уравнением:
x2 – x – 1= 0
Слайд 4Другой пример золотого сечения был обнаружен в пирамиде Хеопса. В сечении знаменитого
сооружения также заложен принцип золотого сечения.
Сумма двух сторон равнобедренного треугольника ABC относится к его основанию также как сумма всех сторон треугольника к сумме равных сторон. Иными словами:
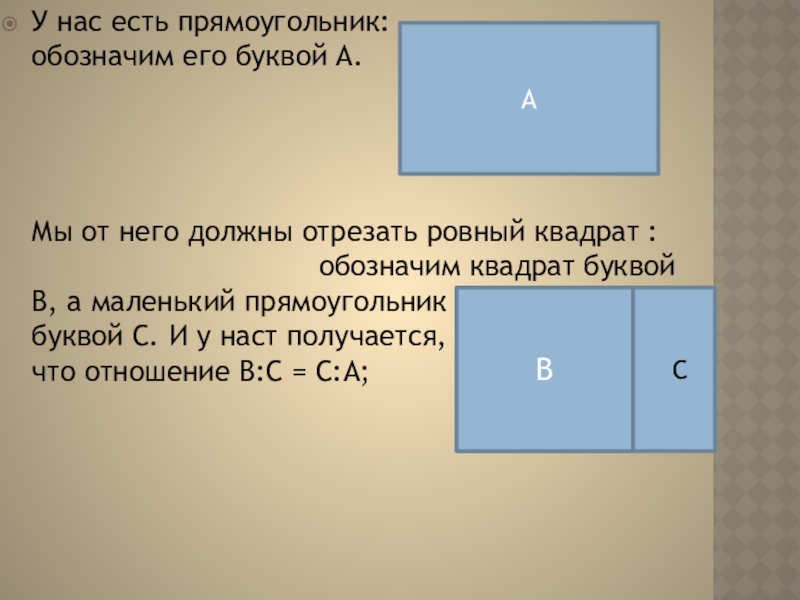
Слайд 5У нас есть прямоугольник: обозначим его буквой A. Мы от него должны отрезать
ровный квадрат :
обозначим квадрат буквой В, а маленький прямоугольник
буквой С. И у наст получается,
что отношение В:С = С:А;
A
С
В
С
Слайд 6 Допустим возьмём пример из жизни: у нас есть скамейка, но мы
не
всегда сядем на неё посередине,
не будем расчитывать я сяду
именно на эту скамейку и именно
посередине .
Мы сядем скраю:
И то место которое у нас останется будет составлять примерно 0,6 от всей скамейки.
Мы сядем скраю:
И то место которое у нас останется будет составлять примерно 0,6 от всей скамейки.
Слайд 7Первый способ — по данной стороне S с помощью транспортира. Проводим прямую и
откладываем на ней AB = S; принимаем эту линию за радиус и этим радиусом из точек A и В описываем дуги: далее с помощью транспортира строим в этих точках углы в 108°, стороны которых пересекутся с дугами в точках С и D; из этих точек радиусом АВ = 5 описываем дуги, которые пересекутся в Е, и прямыми линиями соединяем точки Л, С, Е, D, В.
Полученный пятиугольник — искомый.
Первый способ построения пятиугольника:
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е. Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Второй способ построения пятиугольника:
Первый способ построения пятиугольника:
Второй способ. Проведем окружность радиусом r. Из точки А циркулем проводим дугу радиуса AM до пересечения в точках В и С с окружностью. Соединяем В и С линией, которая пересечет горизонтальную ось в точке Е. Затем из точки Е проводим дугу, которая пересечет горизонтальную линию в точке О. Описываем, наконец, из точки F дугу, которая пересечет окружность в точках Н и К. Отложив по окружности расстояние FO = FH = FK пять раз и соединив точки деления линиями, получим правильный пятиугольник.
Второй способ построения пятиугольника:
Слайд 8Третий способ. В данный круг вписать правильный пятиугольник. Проводим два взаимно перпендикулярных
диаметра АВ и МС. Делим радиус АО точкой Е пополам. Из точки Е, как из центра, проводим дугу окружности радиуса ЕМ и засекаем ею диаметр АВ в точке F. Отрезок MF равен стороне искомого правильного пятиугольника. Раствором циркуля, равным MF, делаем засечки N1, Р1, Q1, К1 и соединяем их прямыми.
Третий способ построения пятиугольника:
Третий способ построения пятиугольника: