- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Симметрия в природе (11 класс)
Содержание
- 1. Презентация по геометрии на тему Симметрия в природе (11 класс)
- 2. Слово «симметрия» от греческого symmetria — соразмерность.
- 3. Словарь иностранных слов «Симметрия - [греч. symmetria]
- 4. Краткий Оксфордский словарь«Симметрия - красота, обусловленная пропорциональностью
- 5. Словарь С.И. Ожегова «Симметрия - соразмерность, пропорциональность
- 6. Осевая симметрия фигурДве точки А и А1
- 7. Осевая симметрия фигурФигура называется симметричной относительно прямой
- 8. Центральная симметрияДве точки А и А1 называются
- 9. Центральная симметрияФигура называется симметричной относительно точки О,
- 10. Симметрия относительно плоскости Две точки А и
- 11. Симметрия относительно плоскости Фигура называется симметричной относительно
- 12. Симметрия относительно плоскости
- 13. Симметрия в природеРадиально-лучевая симметрияБилатеральная симметрия
- 14. Симметрия в природе
- 15. Симметрия в природе
- 16. Симметрия в природе
- 17. Симметрия в природе
- 18. Симметрия в природе
- 19. Симметрия в природе
- 20. Симметрия в природе
- 21. Симметрия в природе
- 22. ВыводВсе, что растет по вертикали, то есть
Слово «симметрия» от греческого symmetria — соразмерность.
Слайд 3Словарь иностранных слов
«Симметрия - [греч. symmetria] - полное зеркальное соответствие
в расположении частей целого относительно средней линии, центра; соразмерность».
![Словарь иностранных слов «Симметрия - [греч. symmetria] - полное зеркальное соответствие в расположении частей целого относительно средней](/img/thumbs/0f0acaad78e5ca974455f4e21be598f0-800x.jpg "Презентация по геометрии на тему Симметрия в природе (11 класс) Словарь иностранных слов «Симметрия - [греч. symmetria] - полное зеркальное соответствие")
Слайд 4Краткий Оксфордский словарь
«Симметрия - красота, обусловленная пропорциональностью частей тела или любого
целого, равновесием, подобием, гармонией, согласованностью».
Слайд 5Словарь С.И. Ожегова
«Симметрия - соразмерность, пропорциональность частей чего-нибудь, расположенных по
обе стороны от середины, центра».
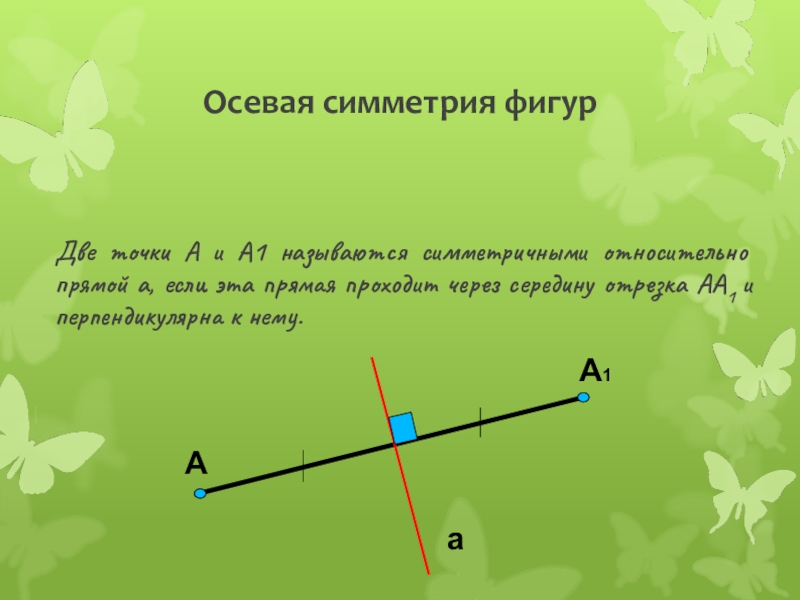
Слайд 6Осевая симметрия фигур
Две точки А и А1 называются симметричными относительно прямой
а, если эта прямая проходит через середину отрезка АА1 и перпендикулярна к нему.
А
А1
а
Слайд 7Осевая симметрия фигур
Фигура называется симметричной относительно прямой а, если для каждой
точки фигуры симметричная ей точка относительно прямой а, также принадлежит этой фигуре.
Слайд 8Центральная симметрия
Две точки А и А1 называются симметричными относительно точки О,
если О – середина отрезка АА1.
О
А
А1
Слайд 9Центральная симметрия
Фигура называется симметричной относительно точки О, если для каждой точки
фигуры симметричная ей точка относительно точки О также принадлежит этой фигуре.
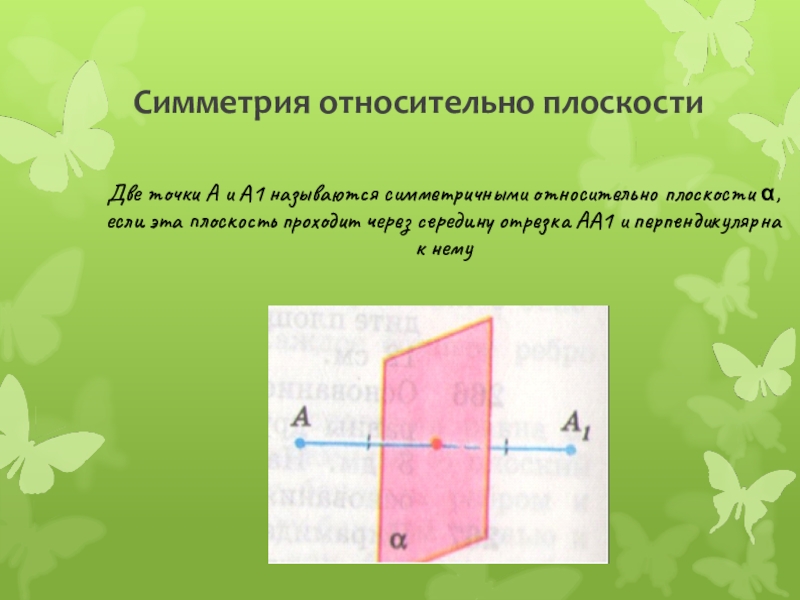
Слайд 10 Симметрия относительно плоскости
Две точки А и А1 называются симметричными относительно
плоскости α, если эта плоскость проходит через середину отрезка АА1 и перпендикулярна к нему
Слайд 11Симметрия относительно плоскости
Фигура называется симметричной относительно плоскости α, если для
каждой точки фигуры симметричная ей точка относительно плоскости, также принадлежит этой фигуре
Слайд 22Вывод
Все, что растет по вертикали, то есть вверх или вниз относительно
земной поверхности, подчиняется радиально-лучевой симметрии в виде веера пересекающихся плоскостей симметрии; все то, что растет горизонтально или наклонно по отношению к земной поверхности подчиняется билатеральной симметрии.
