угол вписанный в окружность.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Угол вписанный в окружность
Содержание
- 1. Презентация по теме Угол вписанный в окружность
- 2. План рассмотрения темы.1. Определение понятий :
- 3. 1. Определение понятий.Угол разбивает плоскость на две
- 4. ООАВ3.Центральным углом в окружности называется плоский
- 5. 2. Доказательство теоремы об угле вписанном в
- 6. Доказательство. Рассмотрим три возможных варианта
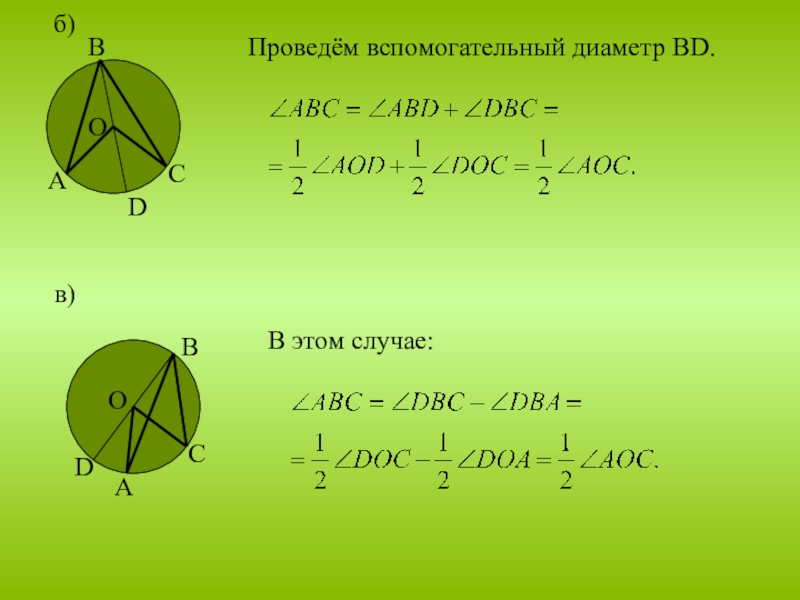
- 7. б) Проведём вспомогательный диаметр ВD.ВСАDОв)В этом случае:ОВСАD
- 8. 3. Следствие доказательства данной теоремы.АВВписанные углы, стороны
План рассмотрения темы.1. Определение понятий : - плоский угол;
Слайд 2План рассмотрения темы.
1. Определение понятий :
- плоский угол;
- дополнительные углы;
- центральный угол;
- дуга окружности;
- градусная мера дуги;
- угол вписанный в окружность.
2. Доказательство теоремы об угле вписанном в окружность.
3. Следствие доказательства данной теоремы.
- дополнительные углы;
- центральный угол;
- дуга окружности;
- градусная мера дуги;
- угол вписанный в окружность.
2. Доказательство теоремы об угле вписанном в окружность.
3. Следствие доказательства данной теоремы.
Слайд 3
1. Определение понятий.
Угол разбивает плоскость на две
части, каждая из
которых называется
плоским углом.
плоским углом.
Плоские углы с общими сторонами
называются дополнительными.
а
b
1.Плоский угол.
2.Дополнительные углы.
Слайд 4
О
О
А
В
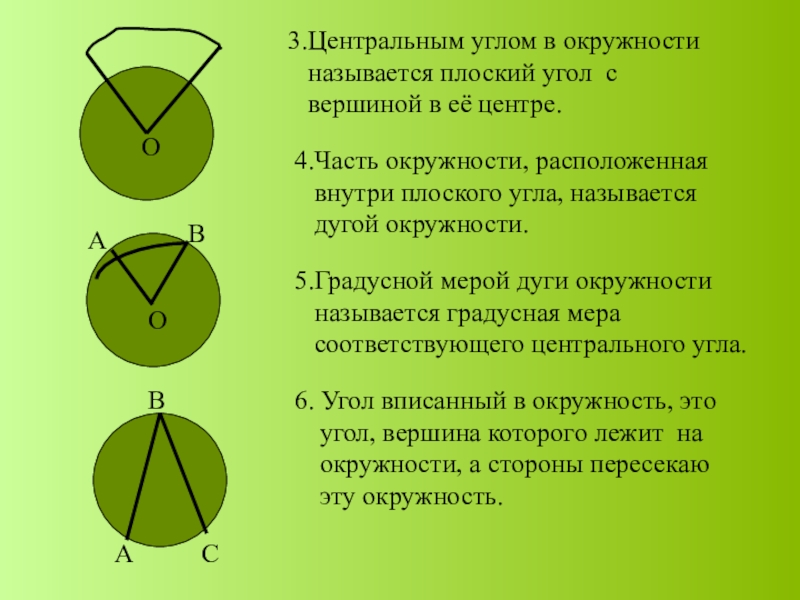
3.Центральным углом в окружности
называется плоский угол с
вершиной в её центре.
4.Часть окружности, расположенная
внутри плоского угла, называется
дугой окружности.
5.Градусной мерой дуги окружности
называется градусная мера
соответствующего центрального угла.
6. Угол вписанный в окружность, это угол, вершина которого лежит на окружности, а стороны пересекаю эту окружность.
А
В
С
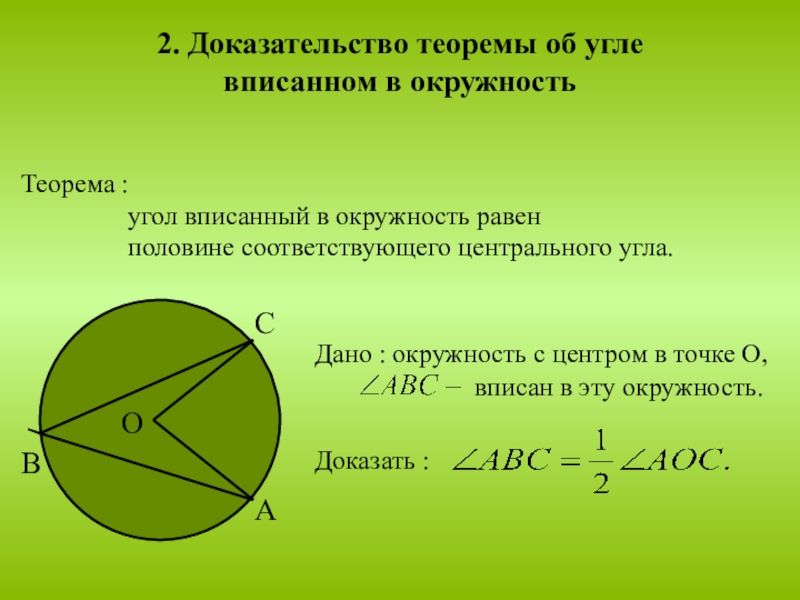
Слайд 52. Доказательство теоремы об угле
вписанном в окружность
Теорема :
угол вписанный в окружность равен
половине соответствующего центрального угла.
половине соответствующего центрального угла.
Дано : окружность с центром в точке О,
Доказать :
В
А
С
О
вписан в эту окружность.
Слайд 6Доказательство.
Рассмотрим три возможных варианта расположения
вписанного угла относительно центра окружности.
а)
В
О
С
А
Сторона угла проходит через центр окружности.
- равнобедренный, т.к. ВО=АО=R.
-внешний для
.
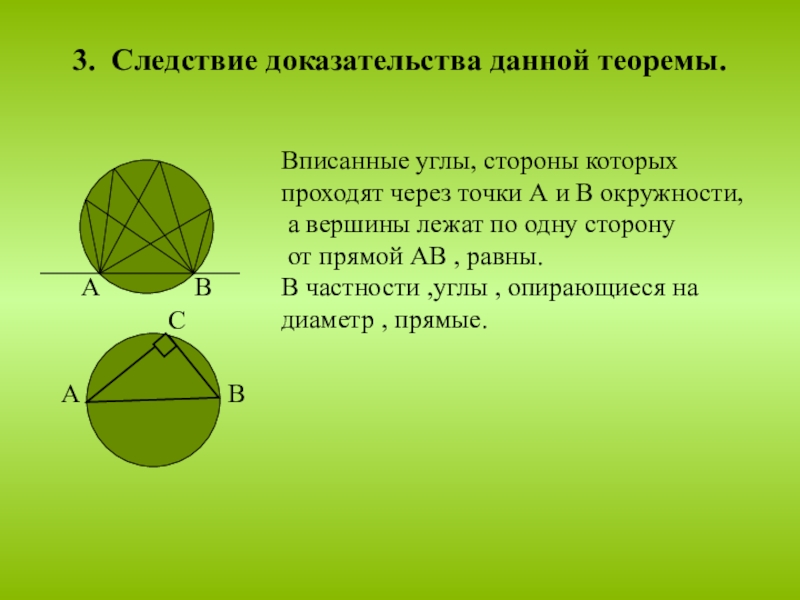
Слайд 83. Следствие доказательства данной теоремы.
А
В
Вписанные углы, стороны которых
проходят через точки
А и В окружности,
а вершины лежат по одну сторону
от прямой АВ , равны.
В частности ,углы , опирающиеся на
диаметр , прямые.
а вершины лежат по одну сторону
от прямой АВ , равны.
В частности ,углы , опирающиеся на
диаметр , прямые.
А
В
С
