- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Задачи по геометрии в вариантах ЕГЭ
Содержание
- 1. Задачи по геометрии в вариантах ЕГЭ
- 2. Задачи по геометрии вариантах ЕГЭ
- 3. Слайд 3
- 4. Из
- 5. Так как АС=ВС, то углы А и
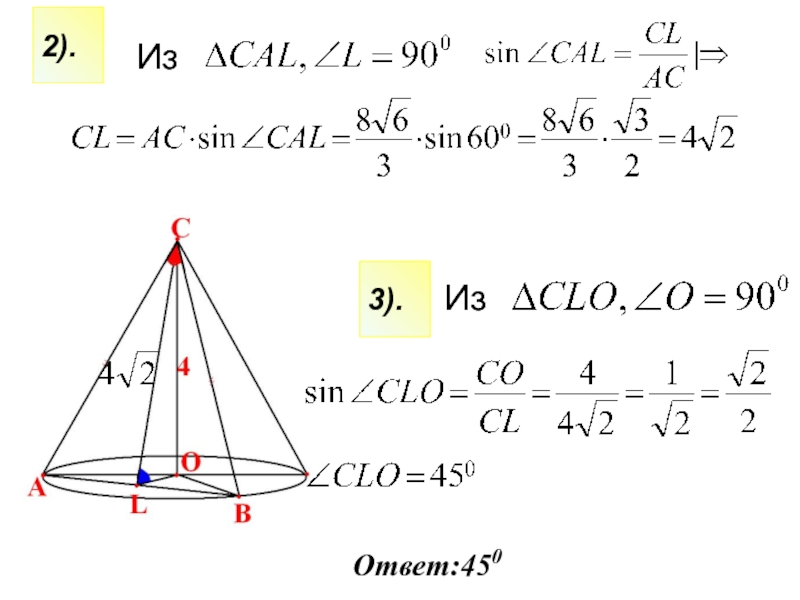
- 6. Из Из 2).3).Ответ:450
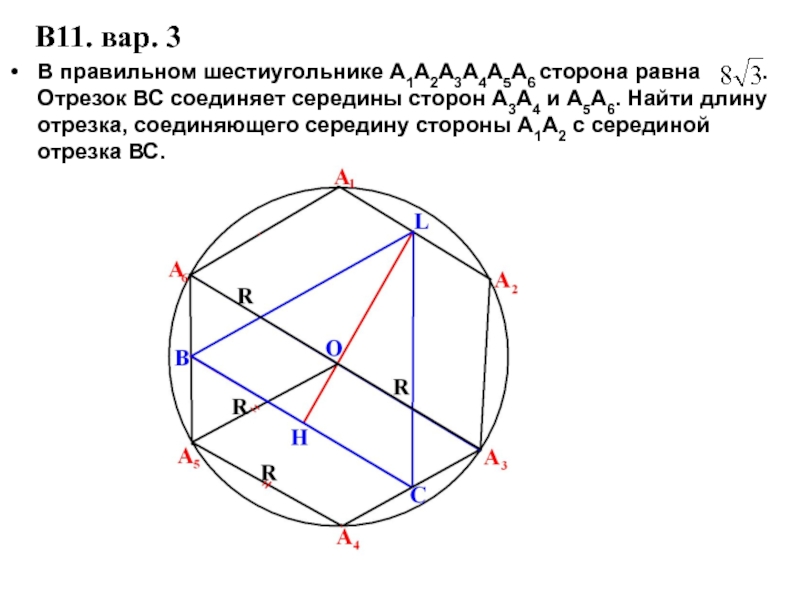
- 7. В11. вар. 3В правильном шестиугольнике А1А2А3А4А5А6 сторона
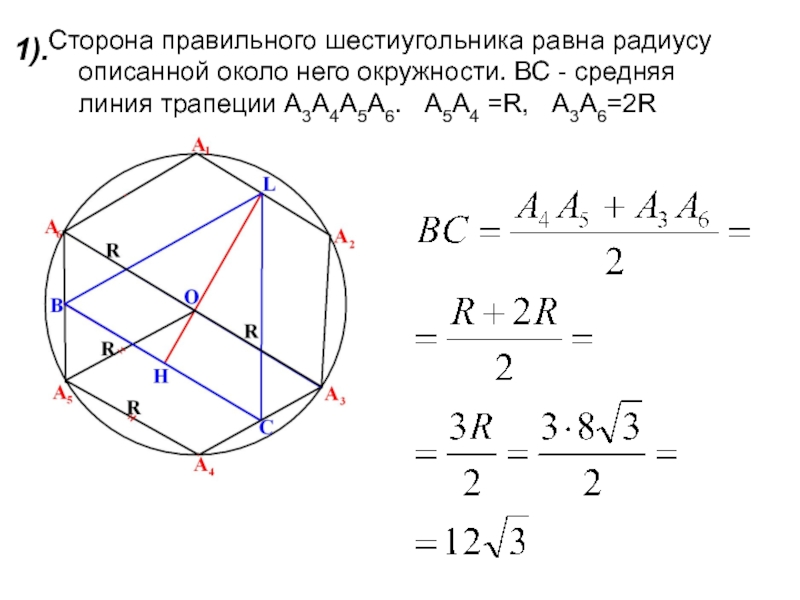
- 8. 1).Сторона правильного шестиугольника равна радиусу описанной около
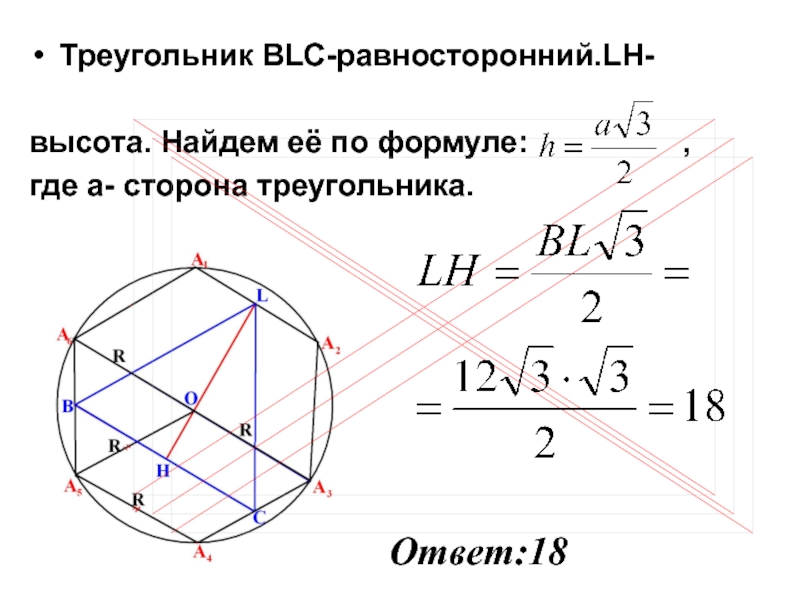
- 9. Треугольник BLC-равносторонний.LH- высота. Найдем её по формуле:
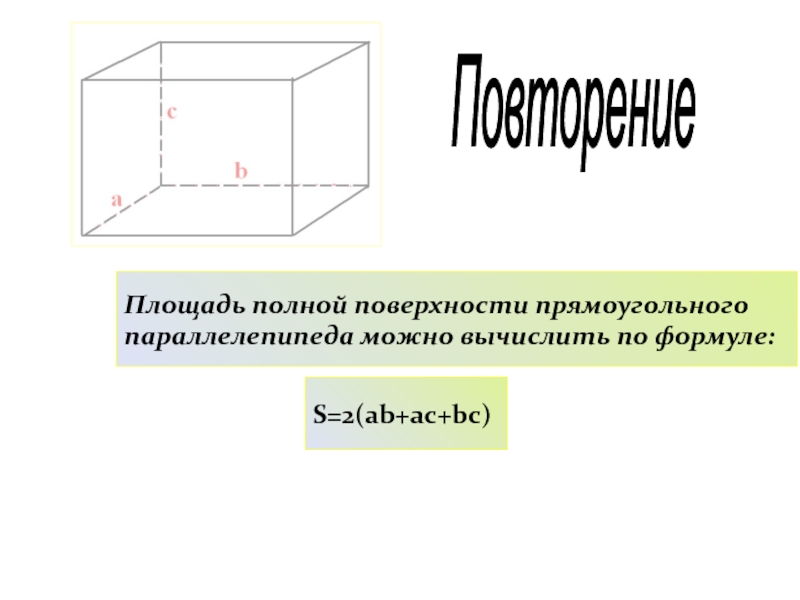
- 10. Площадь полной поверхности прямоугольного параллелепипеда можно вычислить по формуле:S=2(ab+ac+bc)Повторение
- 11. Уравнение плоскости в отрезках:
- 12. Если Ax+By+Cz+D=0 -уравнение плоскости ά, то:Повторение
- 13. 2). (D1B1C):
- 14. Если - острый
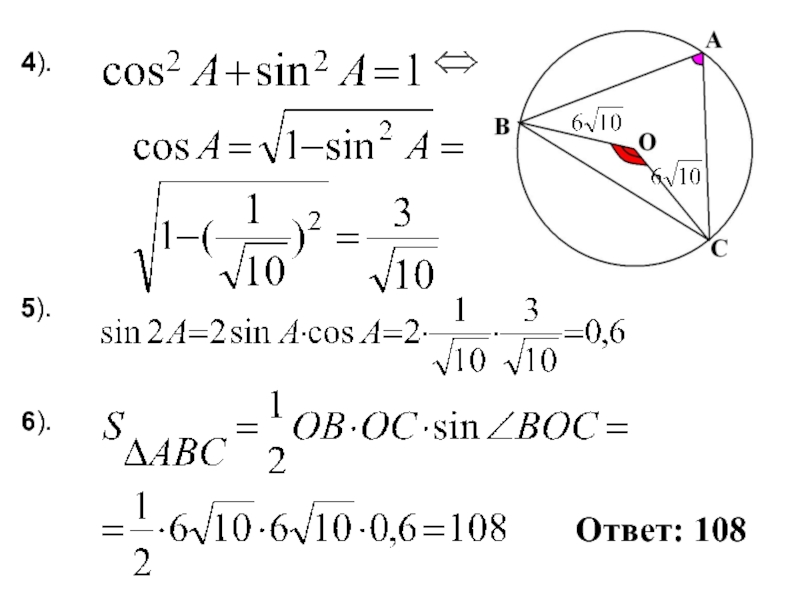
- 15. 2.Градусная мера вписанного угла (ВАС) равна половине
- 16. Площадь треугольника ОВС равна половине произведения его сторон на синус угла между ними.3.Повторение
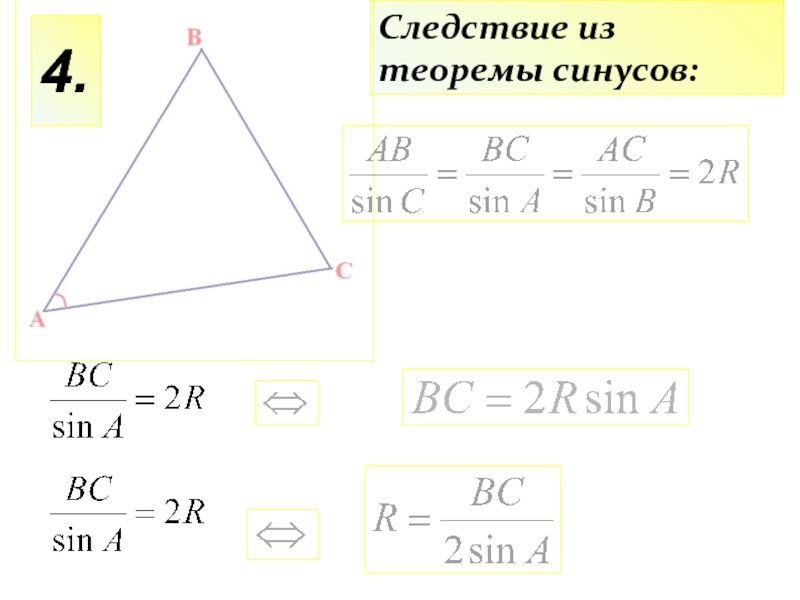
- 17. 4.Следствие из теоремы синусов:
- 18. В
- 19. 6).5).4).Ответ: 108
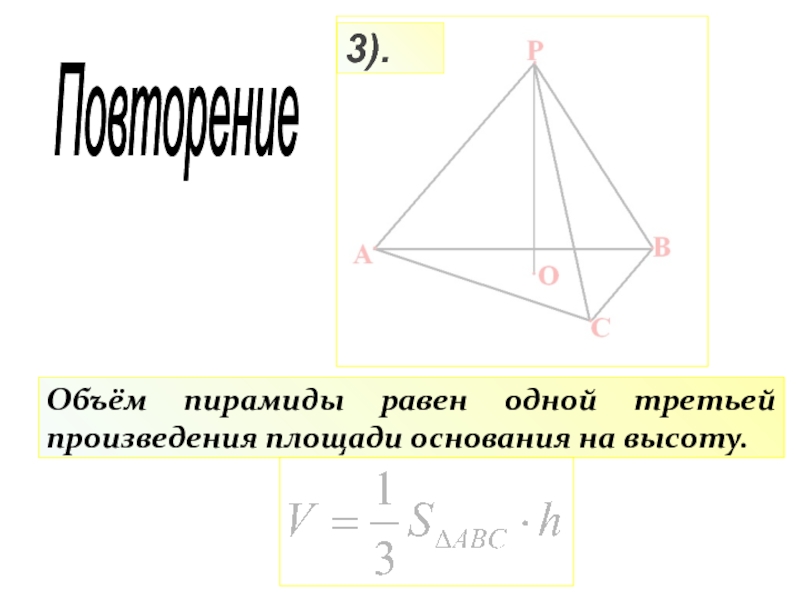
- 20. 3).Объём пирамиды равен одной третьей произведения площади основания на высоту. Повторение
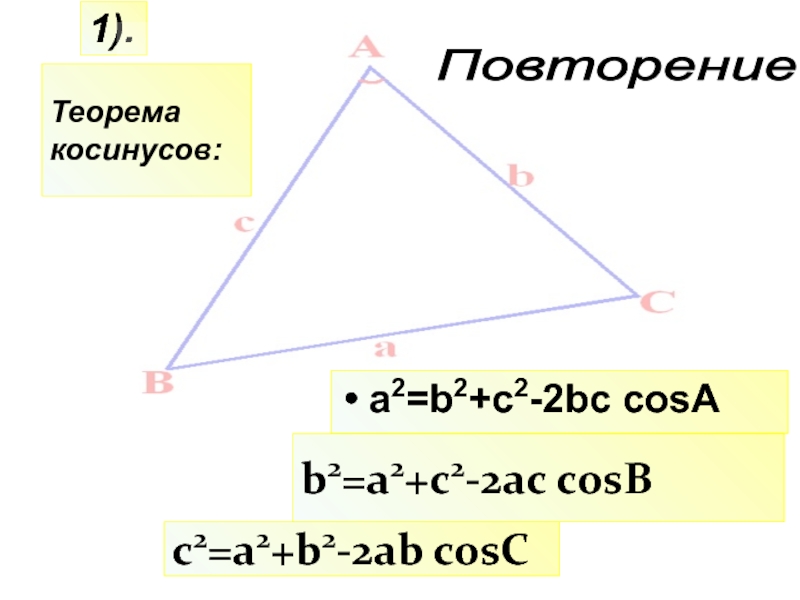
- 21. c2=a2+b2-2ab cosC1).b2=a2+c2-2ac cosBПовторение a2=b2+c2-2bc cosAТеорема косинусов:
- 22. Теорема Пифагора: «В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».c2=a2+b22).Повторение
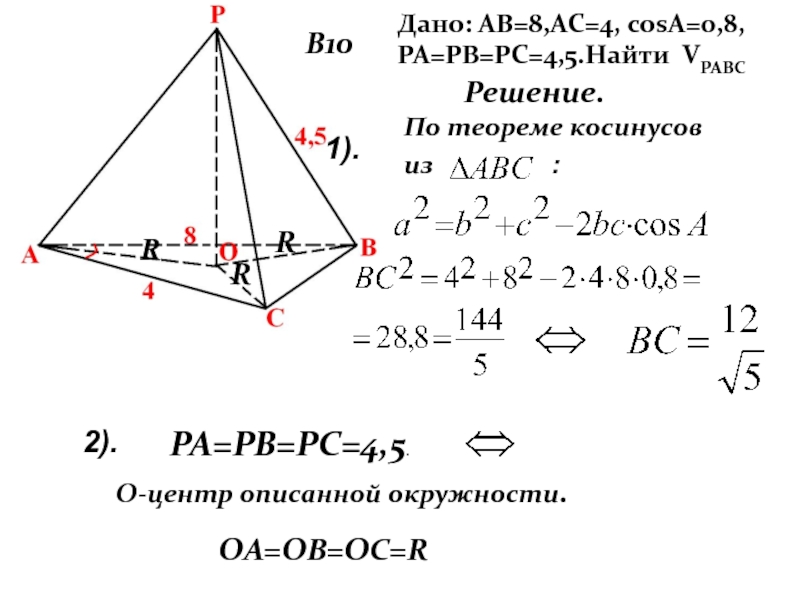
- 23. В10Дано: АВ=8,АС=4, cosA=0,8, РА=РВ=РС=4,5.Найти VРАВС Решение.По теореме
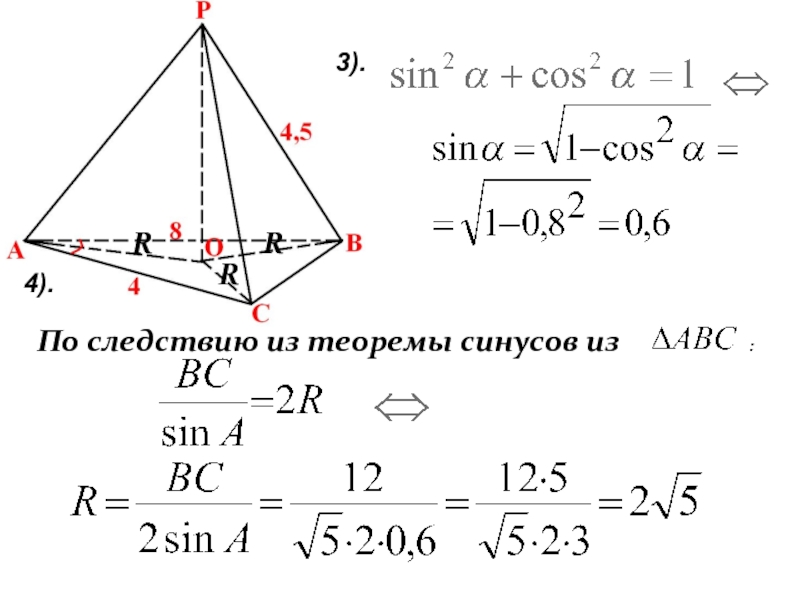
- 24. 4).По следствию из теоремы синусов из
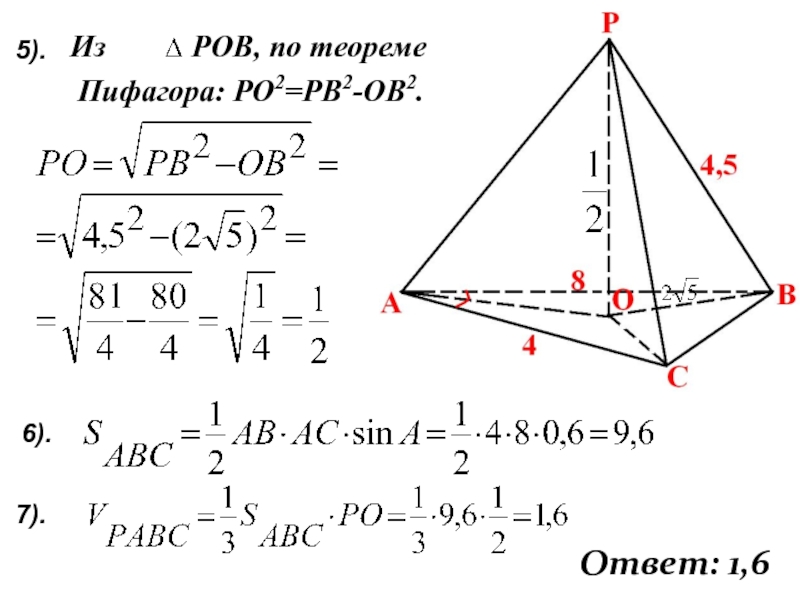
- 25. Из РОВ, по теореме Пифагора: РО2=РВ2-ОВ2.7).Ответ: 1,65).6).
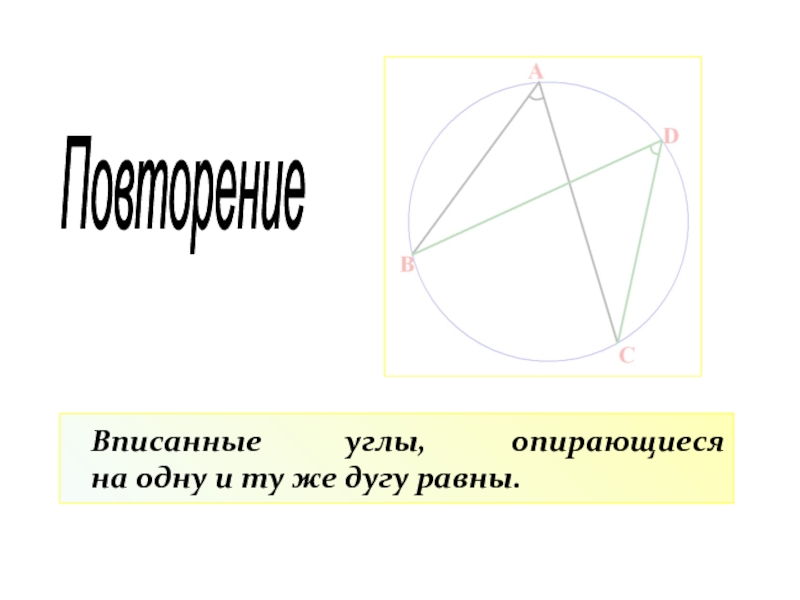
- 26. Вписанные углы, опирающиеся на одну и ту же дугу равны.Повторение
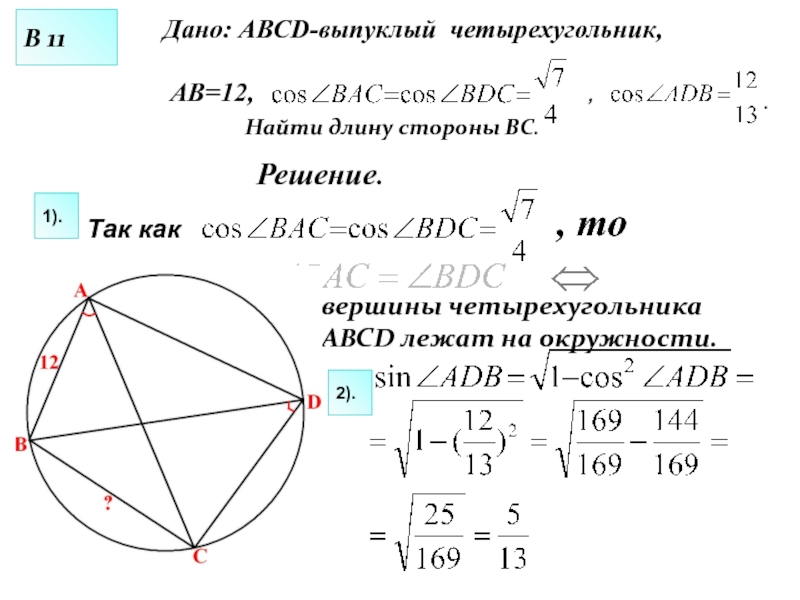
- 27. Дано: АВСD-выпуклый четырехугольник, АВ=12,
- 28. Ответ: 23,4По следствию из теоремы синусов из
- 29. Слайд 29
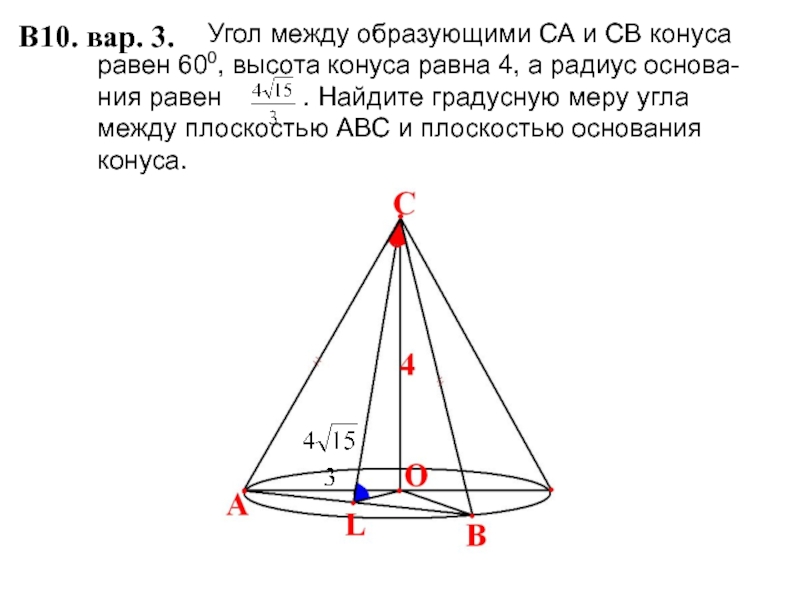
Слайд 3 Угол
В10. вар. 3.
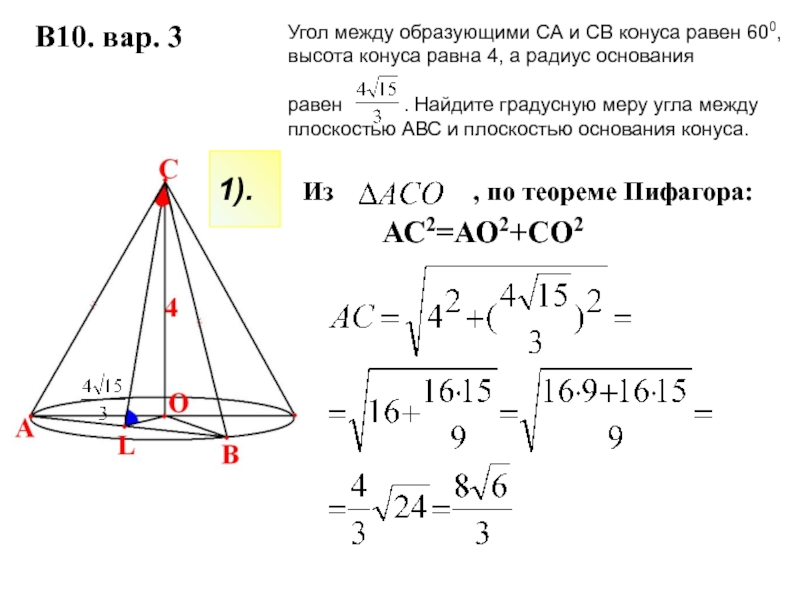
Слайд 4 Из
Угол между образующими СА и СВ конуса равен 600, высота конуса равна 4, а радиус основания
равен . Найдите градусную меру угла между плоскостью АВС и плоскостью основания конуса.
В10. вар. 3
АС2=АО2+СО2
1).
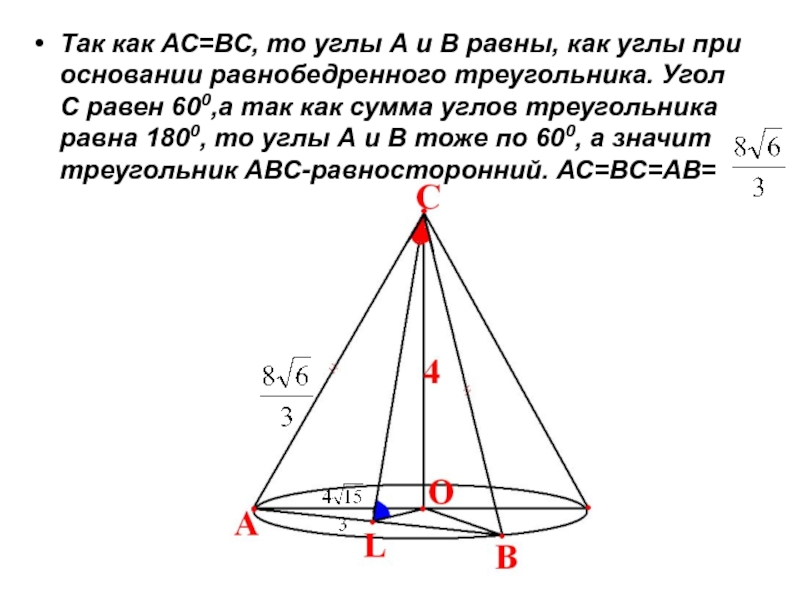
Слайд 5Так как АС=ВС, то углы А и В равны, как углы
Слайд 7В11. вар. 3
В правильном шестиугольнике А1А2А3А4А5А6 сторона равна
Слайд 81).
Сторона правильного шестиугольника равна радиусу описанной около него окружности. ВС -
Слайд 9Треугольник BLC-равносторонний.LH-
высота. Найдем её по формуле:
где а- сторона треугольника.
Ответ:18
Слайд 10Площадь полной поверхности прямоугольного параллелепипеда можно вычислить по формуле:
S=2(ab+ac+bc)
Повторение
Слайд 11Уравнение плоскости в отрезках:
,
где a, b, c –абсцисса, ордината и аппликата
точек пересечения плоскости с осями
координат.
Повторение
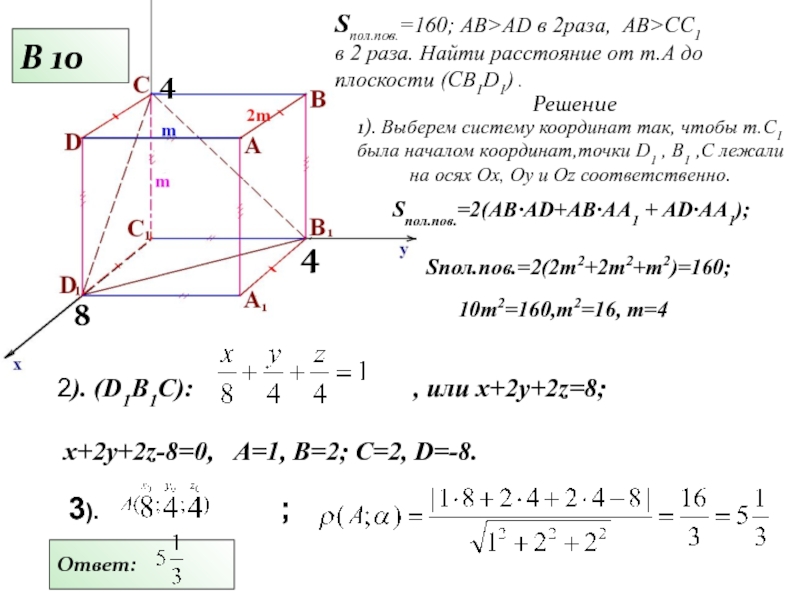
Слайд 132). (D1B1C):
Sпол.пов.=160; АВ>AD в 2раза, AB>CC1
в 2 раза. Найти расстояние от т.А до плоскости (СВ1D1) .
Решение
Sпол.пов.=2(AB·AD+AB·AA1 + AD·AA1);
8
4
3). ;
Ответ:
B 10
Sпол.пов.=2(2m2+2m2+m2)=160;
10m2=160,m2=16, m=4
4
1). Выберем систему координат так, чтобы т.С1 была началом координат,точки D1 , B1 ,C лежали на осях Ох, Оу и Оz соответственно.
Слайд 14Если - острый угол, то
Некоторые тригонометрические тождества:
1.а).
Если - острый угол, то
б).
в).
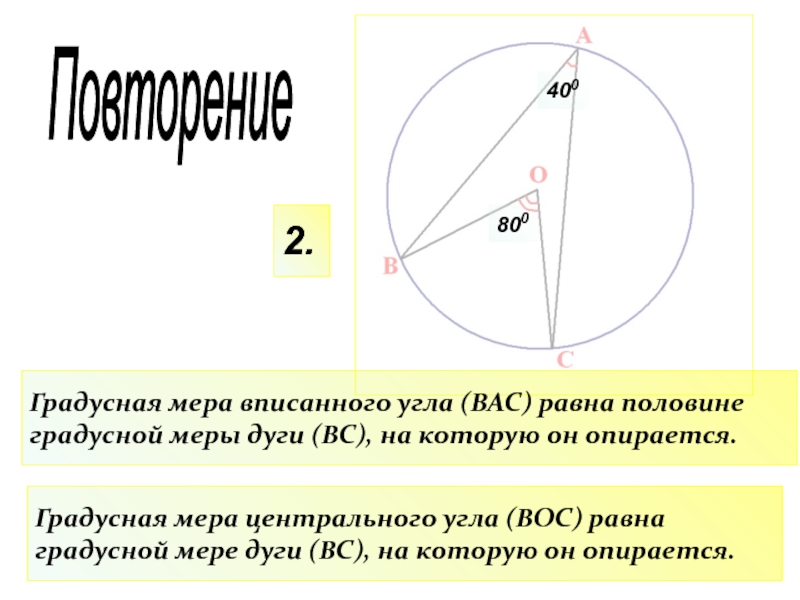
Слайд 152.
Градусная мера вписанного угла (ВАС) равна половине градусной меры дуги (ВС),
Градусная мера центрального угла (ВОС) равна градусной мере дуги (ВС), на которую он опирается.
400
800
Повторение
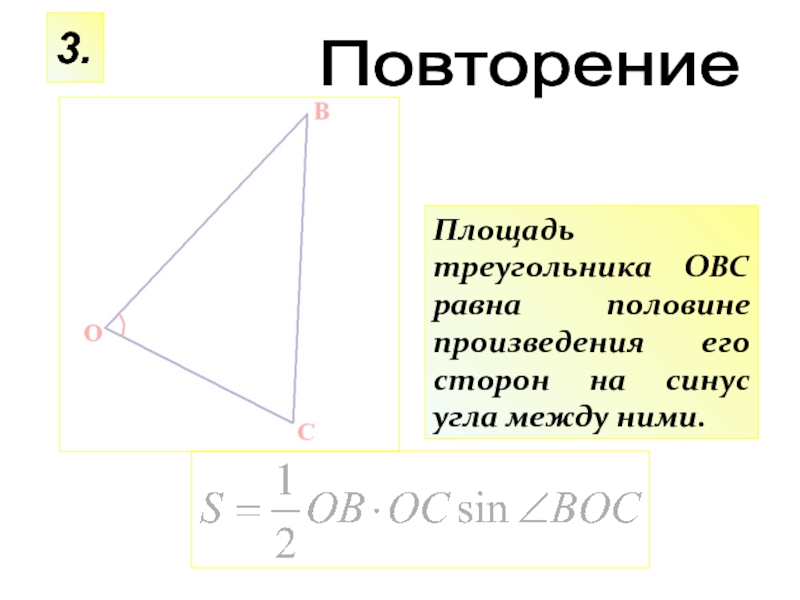
Слайд 16Площадь треугольника ОВС равна половине произведения его сторон на синус угла
3.
Повторение
Слайд 18В ,
По следствию из теоремы синусов:
1).
B 11
Решение.
3).
,как вписанный угол.
-как центральный, следовательно:
2).
12
Слайд 22Теорема Пифагора:
«В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
c2=a2+b2
2).
Повторение
Слайд 23В10
Дано: АВ=8,АС=4, cosA=0,8, РА=РВ=РС=4,5.Найти VРАВС
Решение.
По теореме косинусов
из
2).
1).
РА=РВ=РС=4,5.
OА=OВ=OС=R
O-центр описанной окружности.
R
R
R
Слайд 27Дано: АВСD-выпуклый четырехугольник, АВ=12,
, то
Найти длину стороны ВС.
Решение.
2).
1).
Так как
вершины четырехугольника ABCD лежат на окружности.
В 11
.
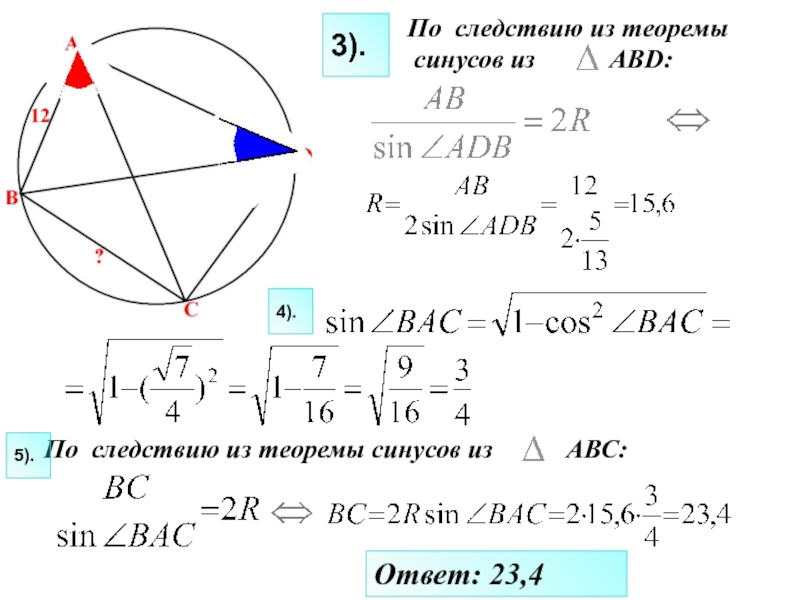
Слайд 28Ответ: 23,4
По следствию из теоремы синусов из
5).
4).
По следствию из теоремы
синусов из АВD:
3).
Слайд 29
I вариант.
В , ВС=6, ctgA=3. Найти , где О- центр описанной около треугольника АВС окружности.
Самостоятельная работа.