- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад к занятиям по геометрии( внеурочка)
Содержание
- 1. Презентация к занятиям по геометрии( внеурочка)
- 2. Цель работы Я выбрала тему
- 3. Историческая справка задач на построение В XVII
- 4. О решении задач на построениеРешение задач на построение состоит из 4 этапов:АнализПостроениеДоказательствоИсследование
- 5. Простейшие задачи на построение с помощью циркуля
- 6. О геометрических построениях с использованием одной линейки
- 7. Теорема Дезарга Если прямые,
- 8. Доказательство теоремы Дезарга Докажем теорему
- 9. Для доказательства принадлежности
- 10. Для Δ SАС
- 11. Модификации теоремы Дезарга
- 12. Теорема 2. Дано: ABC
- 13. Теорема 3. Дано: ABC и
- 14. Теорема 4. Дано: ABC
- 15. Применение теоремы Дезарга для построения
- 16. Решение. Анализ. Пусть задача решена и прямая
- 17. В этой задаче первоначальный рисунок ничего не
- 18. (С /С) ∩ (В/В) = S, S
- 19. Слайд 19
- 20. Слайд 20
- 21. Задача с недоступными элементами
- 22. Задача. Даны
- 23. Так как точки М и L лежат
- 24. Построение: 1.
- 25. Поляра Четыре точки A, B, C,
- 26. Доказательство: Введем систему координат с началом в
- 27. корни x1 и x2 которого равны абсциссам
- 28. Отсюда, учитывая, что
- 29. Но в этом случае
- 30. Вывод В ходе
- 31. Список литературы 1. Л.С. Атанасян «Геометрия 7-9»
Слайд 1
Задачи на построение с помощью одной линейки
Шилина Анна
Учитель: Иванченко И.А.
Слайд 2Цель работы
Я выбрала тему «Задачи на построение»,
Слайд 3Историческая справка задач на построение
В XVII – XIX вв. Леонардо
В XVIII веке швейцарец Ламберт рассматривал некоторые задачи на построение на ограниченном куске плоскости.
Разработкой методов решения задачи на построение математики занимаются еще со времен Древней Греции. Уже математики школы Пифагора (VI в. до н.э.) решили довольно сложную задачу построения правильного пятиугольника.
Слайд 4О решении задач на построение
Решение задач на построение состоит из 4
Анализ
Построение
Доказательство
Исследование
Слайд 5Простейшие задачи на построение с помощью циркуля и линейки
Задача 1. На
Задача 2. Отложить от данного луча угол, равный данному
Задача 3. Построить биссектрису данного угла
Задача 4. Построить прямую, проходящую через данную точку и перпендикулярную к данной прямой
Слайд 6О геометрических построениях с использованием одной линейки
Изучение геометрических
Слайд 7Теорема Дезарга
Если прямые, соединяющие соответственные вершины двух
S
B
A
C
U
A/
B/
C/
V
W
Слайд 8Доказательство теоремы Дезарга
Докажем теорему Дезарга с помощью теоремы
Теорема Менелая. Точки A1 , B1 и C1 , расположенные соответственно на прямых BC, CA, AB и не совпадающие с вершинами треугольника ABC, лежат на одной прямой тогда и только тогда, когда (см. рис.)
AB1 CA1 BC1
* * = -1.
B1C A1B C1A
C1
A
B
A1
C
B1
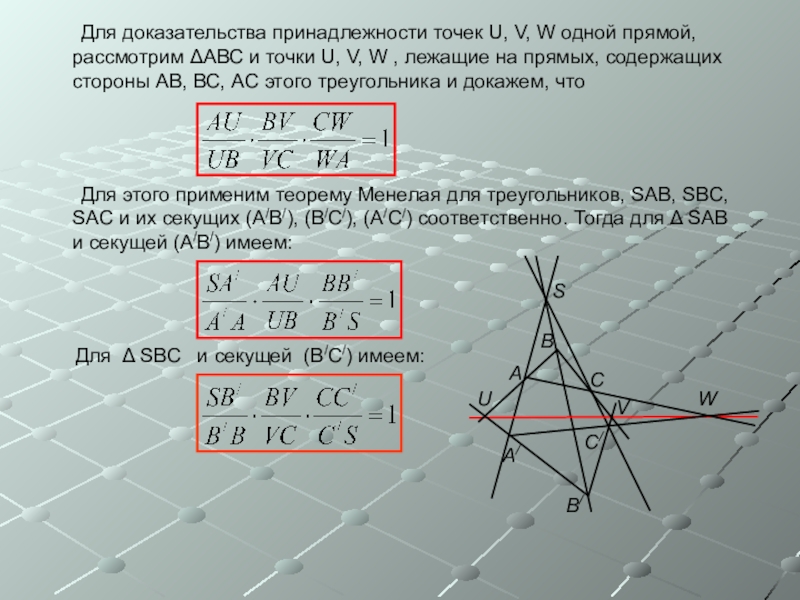
Слайд 9 Для доказательства принадлежности точек U, V, W
Для этого применим теорему Менелая для треугольников, SАВ, SBC, SAC и их секущих (A/B/), (В/С/), (А/С/) соответственно. Тогда для Δ SАВ и секущей (А/В/) имеем:
Для Δ SВС и секущей (В/С/) имеем:
S
A
B
C
W
U
V
A/
B/
C/
Слайд 10 Для Δ SАС и секущей (А/С) имеем:
Умножим на и поделим
на Получаем:
В итоге получили равенство
S
B
A
C
U
A/
B/
C/
V
W
Слайд 11Модификации теоремы Дезарга
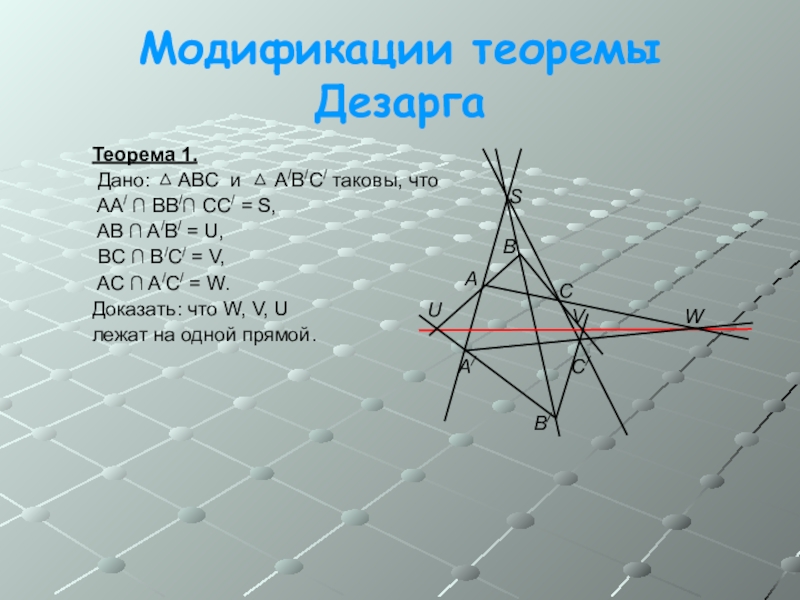
Теорема 1.
AA/ ∩ BB/∩ CC/ = S,
AB ∩ A/B/ = U,
BC ∩ B/C/ = V,
AC ∩ A/C/ = W.
Доказать: что W, V, U
лежат на одной прямой.
S
B
C
A
U
V
W
A/
C/
B/
Слайд 12Теорема 2.
Дано: ABC и A/B/C/
AA/ // BB/ // CC/ ,
AB ∩ A/B/ = X,
BC ∩ B/C/ = Y,
AC ∩ A/C/ = Z.
Доказать: X, Y, Z
лежат на одной прямой.
A
B
C
X
Y
Z
C/
B/
A/
Слайд 13
Теорема 3.
Дано: ABC и A/B/C/
AA/
AB ∩ A/B/ = X,
BC ∩ B/C/ = Y,
AC // A/C/
Доказать: XY//AC
C
B
A
S
Y
X
A/
B/
C/
Слайд 14Теорема 4.
Дано: ABC и A/B/C/
AB // A/B/,
BC // B/C/,
Доказать: AC // A/C/
Теорема 5.
Дано: ABC и A/B/C/
AA/ // BB/ // CC/ ,
AB // A/B/ ,
AC // A/C/
Доказать: BC//B/C/
S
B
A
C
B/
C/
A/
A
B
C
A/
B/
C/
Слайд 15
Применение теоремы Дезарга для построения параллельных прямых (с помощью одной линейки)
Задача. Даны две различные параллельные прямые а и b и точка А, не лежащая на них. Через точку А проведите прямую, параллельную данным прямым.
Слайд 16Решение. Анализ. Пусть задача решена и прямая с проходит через точку
Вспомним теорему Дезарга, где треугольники содержат одну пару параллельных сторон (см.теорема3), сопоставим этот рис. и рисунок, иллюстрирующий теорему.
Теорема 3
a
c
b
A
●
C
B
A
S
Y
X
A/
B/
C/
Слайд 17В этой задаче первоначальный рисунок
ничего не выражает. В нашем случае
прямые а и в – это прямые,
на которых лежат две
соответственные стороны треугольников
с осью с. Тогда точка А является точкой
пересечения одной пары
соответственных сторон.
Ещё одна пара соответственных сторон должна
пересекаться в точке, также лежащей на с.
Построение, таким образом, сводится к
построению двух треугольников, одна
пара соответственных сторон которых
лежит на прямых а и в. Поэтому на прямых
а и в возьмем произвольные отрезки:
[С1В1] ∈ а, [СВ] ∈ в в качестве
соответственных
сторон, а вторая пара сторон пересекается
в точке А.
a
c
b
A
●
C
B
A
S
Y
X
A/
B/
C/
Слайд 18(С /С) ∩ (В/В) = S, S – точка, в которой
(Теорема Дезарга, см. рис.)
S
A
B
C
W
U
V
A/
B/
C/
Слайд 19 Построение:
Берем точки С1,
Берем точки С, В, ∈ в
S = (СС1) ∩ (ВВ1)
Проведем произвольную прямую l ∍ S
О1 = l ∩ (С1А)
О = l ∩ (СА)
6. (В1О1) ∩ (ВО) = А1
(АА1) = с – искомая
l
Доказательство:
Рассмотрим ΔС1О1В1 и Δ СОВ. (СС1) ∩ (ВВ1) ∩ (ОО1) = S по построению. Точки А = (С1О1) ∩ (СО) и А1 = (В1О1) ∩ (ВО) определяют прямую с. Поскольку (С1В1) // (СВ), то с // а // в.
С1
В1
a
C
B
b
S
А
О
О1
А1
Слайд 20
Задача всегда имеет единственное решение, так как через данную точку можно провести единственную прямую, параллельную данной.
Слайд 21Задача с недоступными элементами
Точку называют недоступной, если
Слайд 22
Задача. Даны две прямые а и
Решение. Анализ. Пусть задача решена и прямая с проходит через точку М и точку L (см. рис.) Для проведения анализа вспомним теорему Дезарга и сделаем к этой теореме рисунок.
недоступная часть
M c
L
b
a
Слайд 23Так как точки М и L лежат на одной прямой, то
L
b
a
M
S
B
C
A
U
V
W
A/
C/
B/
Слайд 24 Построение:
1. Возьмем точки А,
2. Точка S = (АА/) ∩ (ВВ/).
3. Проведем произвольную прямую l: S ∈ l.
4. С1 = (В/М) ∩ l,
С = (ВМ) ∩ l.
5. (АС) ∩ (А/С/) = М1
(ММ1) = с – искомая.
Доказательство:
Рассмотрим Δ АВС и Δ А/В/С/.
В них:
(ВВ/) ∩ (АА/) ∩ (СС/) = S
(АС) ∩ (А/С/) = М1,
(ВС) ∩ (В/С/) = М,
(АВ) ∩ (А/В/) = а ∩ в = L,
следовательно, по теореме 1 точки М, М1 и L лежат на одной прямой.
a
A
B
b
А/
В/
S
l
L
M
С
С/
М1
Слайд 25Поляра
Четыре точки A, B, C, D, лежащие на одной
AC AD
: = -1.
CB DB
Задача.
Из данной точки A проведены к данной окружности с центром O касательные AK1 , AK2 и секущая, пересекающая окружность в точках C и D, а отрезок K1K2 – в точке B. Докажите, что точки A, B, C и D образуют гармоническую четверку.
Слайд 26Доказательство: Введем систему координат с началом в точке A, как показано
Пусть B1, C1, D1 – проекции точек B, C, D
на ось абсцисс. Докажем, что точки
A, B1, C1, D1 образуют гармоническую
четверку. Отсюда сразу же последует,
что точки A, B, C, D также образуют
гармоническую четверку.
Уравнение окружности запишем в виде
(x – a)2 + y2 = R2 (2)
где a = AO, R – радиус окружности, а уравнение секущей AD – в виде
y = kx (3)
где k – некоторое число. Координаты точек C и D удовлетворяют
уравнениями (2) и (3). Если подставить y = kx в уравнение (2), то придем к
квадратному уравнению
(1 + k2) x2 – 2ax + a2 – R2 = 0 (4)
x
y
A
K2
C
K1
D
B
D1
O
B1
C1
Слайд 27корни x1 и x2 которого равны абсциссам точек C и D,
AC1 = x1, AD1 = x2.
По теореме Виета
2a a2 – R2
x1 + x2 = , x1x2 = ,
1+ k2 1 + k2
2x1x2 a2 – R2
откуда = (5)
x1+ x2 a
Рассматривая прямоугольный треугольник AOK1 , нетрудно
a2 – R2
установить, что AB1 = . Поэтому если положить AB1= x0 ,
a
то равенство (5) можно записать в виде
2x1x2
= x0, или x1(x2 – x0) – x2(x0 – x1) =0.
x1+x2
Слайд 28 Отсюда, учитывая, что
получаем:
AC1 * B1D1 – AD1* C1B1 =0,
а это и означает, что точки A, B1 , C1 , D1 образуют гармоническую четверку.
2x1x2
Замечание. Равенство = x0 можно доказать и не прибегая
x1 + x2
к рассмотрению треугольника AOK1. В самом деле, соотношение
2x1x2 a2 – R2 2x1x2
= показывает, что величина не зависит от
x1+ x2 a x1 + x2
k, т.е.имеет одно и то же значение для любой прямой, описываемой уравнением y = kx. Возьмем k таким, чтобы уравнение y = kx было уравнением касательной AK1.
Тогда оба корня x1 и x2 квадратного уравнения
(1 + k2) x2 – 2ax + a2 – R2 = 0 будут равны абсциссе точки K1 , т.е. будут равны x0.
Слайд 29 Но в этом случае
= = x0 ,
x1 + x2 x0+x0
2x1x2
а значит, и для любой другой прямой = x0
x1 + x2
Прямая K1K2 называется полярой данной точки A относительно данной окружности. Если точка B не лежит на поляре, а прямая AB пересекает окружность в точках C и D, то можно сделать такой вывод:
если данная точка A лежит вне данной окружности, то множество точек B, для каждой из которых точки пересечения прямой AB и окружности гармонически разделяют точки A и B, представляет собой часть поляры точки A относительно данной окружности, лежащую внутри этой окружности.
Слайд 30Вывод
В ходе изучения темы «Задачи
Слайд 31Список литературы
1. Л.С. Атанасян «Геометрия 7-9» М., Просвещение , 1991.
2.
3. Д.И. Перепелкин «Курс элементарной геометрии», часть 1 - «Геометрия на плоскости», Москва 1948 год.
4. Избранные вопросы геометрии (Пособие для учителя) М., 1991.
5. Т.Л. Агафонова и др. «Задачи по объединенному курсу геометрии» (Учебное пособие, часть 4), Ярославль, 1989.
6. Сборник задач по геометрии, часть 2, под ред. Л.С. Атанасяна, М., Просвещение, 1975.
7. Л.С. Атанасян, В.Т. Базылев «Геометрия» ч.2, М., Просвещение, 1987.
Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев, И.И.Юдина «Геометрия. Доп. главы к учебнику 9 кл.» 4 – е изд. – М.: Вита – Пресс, 2004, стр.43, 46-50.
Ресурсы Интернета.