Л.Н.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Проект по математике Все о треугольниках
Содержание
- 1. Проект по математике Все о треугольниках
- 2. Проблема: Выяснить, насколько важна данная
- 3. СодержаниеВиды треугольников;Свойства треугольников;Прямоугольный треугольник;Равнобедренный треугольник;Правильный треугольник;Равенство треугольников;Медианы;Высоты;Биссектрисы;Средняя
- 4. Виды треугольниковПо углам:Тупоугольный – треугольник, у которого
- 5. Виды треугольниковПо сторонам:Разносторонний – треугольник, у которого
- 6. Свойства треугольниковСумма углов треугольника равна 1800
- 7. Прямоугольный треугольникСторона прямоугольного треугольника, противолежащая прямому углу,
- 8. Свойства прямоугольного треугольникаМедиана, проведённая к гипотенузе прямоугольного
- 9. Признаки прямоугольных треугольниковЕсли квадрат одной из сторон
- 10. Свойства равнобедренного треугольникаУглы при основании равны.Высота, проведенная
- 11. Свойства правильного треугольникаВсе углы равностороннего треугольника равны
- 12. Признаки равенства треугольниковПо двум сторонам и углу
- 13. МедианыМедианы треугольника пересекаются в одной точке (центре
- 14. БиссектрисыВсе биссектрисы треугольника пересекаются в одной точке
- 15. Средняя линия Средняя линия параллельна третьей стороне и равна ее половине.
- 16. Серединный перпендикулярВсе серединные перпендикуляры сторон треугольника пересекаются
- 17. Площадь треугольникаS∆ = 0,5 aha= 0,5 bhb=
- 18. Подобные треугольникиОпределение. Два треугольника называются подобными, если их
- 19. Окружность, описанная около треугольникаОколо каждого треугольника
- 20. Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.44 – внешний угол
- 21. Медианой треугольника называется отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.АВСВ1ВВ1 – медиана треугольника
- 22. Высотой треугольника называется отрезок перпендикуляра, опущенного из вершины треугольника на прямую, содержащую противолежащую сторону.АВССС1 - высота
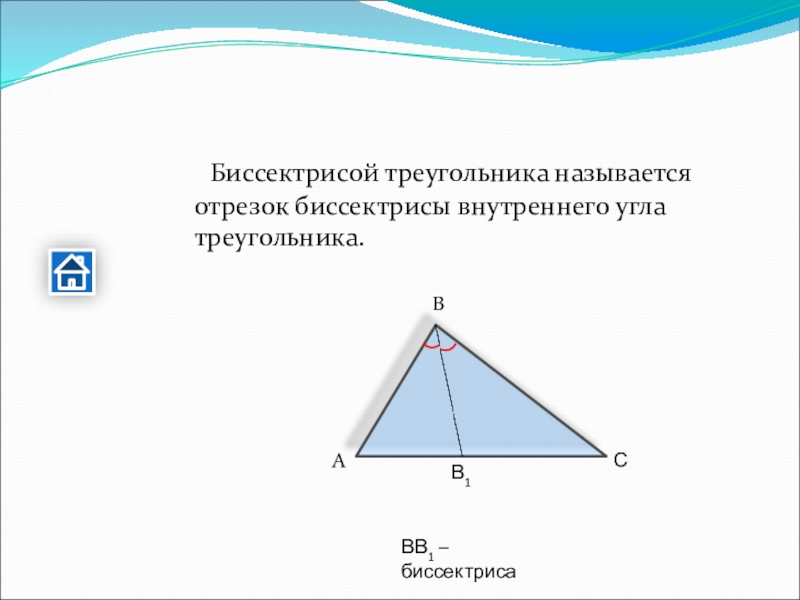
- 23. Биссектрисой треугольника называется отрезок биссектрисы внутреннего угла треугольника.АВВВ1 – биссектриса
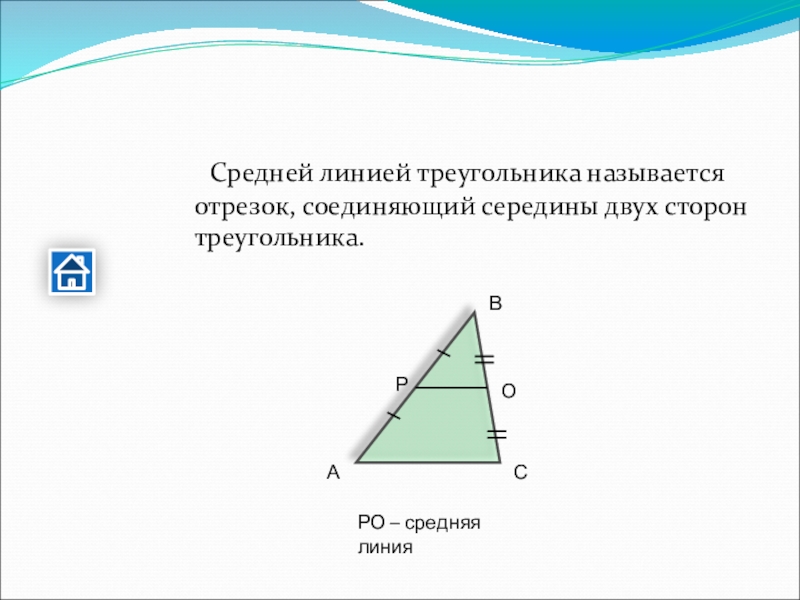
- 24. Средней линией треугольника называется отрезок, соединяющий середины двух сторон треугольника.АВСРОРО – средняя линия
- 25. Серединным перпендикуляром называется прямая, перпендикулярная стороне треугольника и делящая её пополам.АВСВ1
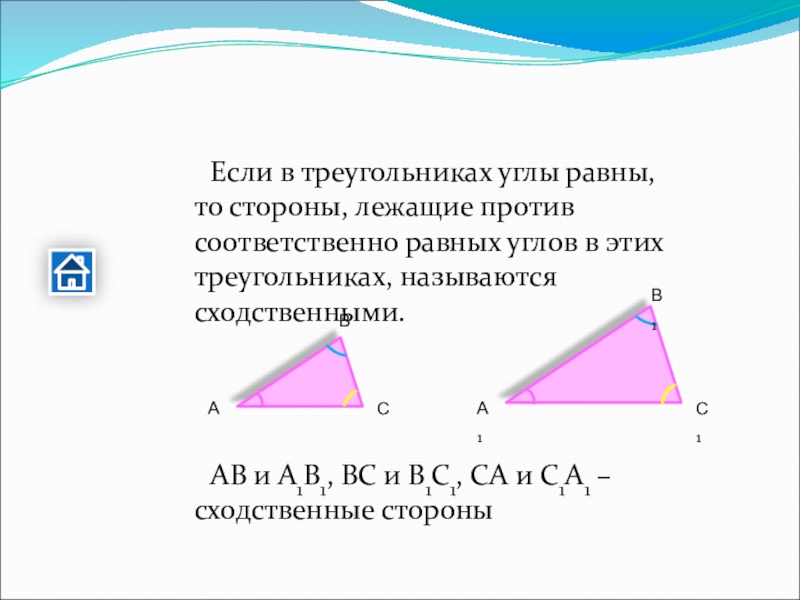
- 26. Если в треугольниках углы равны, то стороны,
- 27. ЛитератураГеометрия, 7-9: учеб. для общеобразоват. учреждений/ Л.С.
Проблема: Выяснить, насколько важна данная тема при подготовке к ОГЭ. Цели: Систематизировать понятия по теме «Все о треугольниках»; Показать практическое применение данного материала при решении задач при подготовке к ОГЭ;Научиться сравнивать треугольники между
Слайд 1Проект на тему:
«Всё о треугольниках»
Выполнила:
Ученица 9кл
Струговской ООШ
Карцева Полина.
Руководитель: Аврамец
Слайд 2Проблема: Выяснить, насколько важна данная тема при подготовке к ОГЭ.
Цели:
Систематизировать понятия по теме «Все о треугольниках»;
Показать практическое применение данного материала при
решении задач при подготовке к ОГЭ;
Научиться сравнивать треугольники между собой;
Выяснить, каковы особенности каждого треугольника.
Слайд 3Содержание
Виды треугольников;
Свойства треугольников;
Прямоугольный треугольник;
Равнобедренный треугольник;
Правильный треугольник;
Равенство треугольников;
Медианы;
Высоты;
Биссектрисы;
Средняя линия;
Серединный перпендикуляр;
Площадь треугольника;
Подобие
треугольников;
Окружность, вписанная в треугольник;
Окружность, описанная около треугольника.
Окружность, вписанная в треугольник;
Окружность, описанная около треугольника.
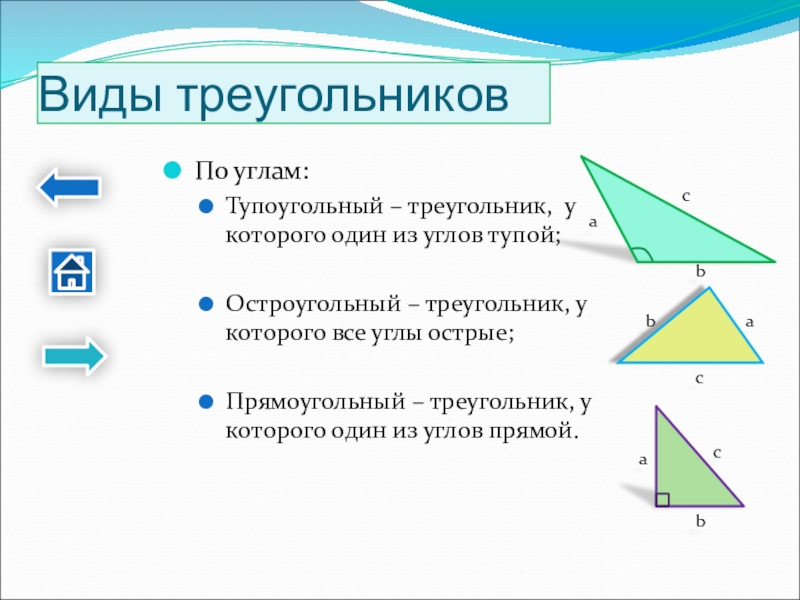
Слайд 4Виды треугольников
По углам:
Тупоугольный – треугольник, у которого один из углов тупой;
Остроугольный – треугольник, у которого все углы острые;
Прямоугольный – треугольник, у которого один из углов прямой.
а
b
с
а
b
с
а
b
с
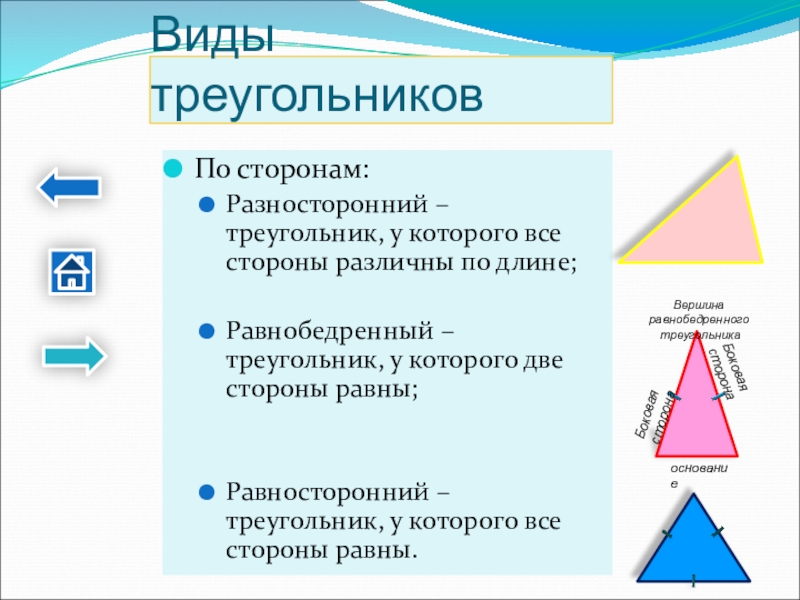
Слайд 5Виды треугольников
По сторонам:
Разносторонний – треугольник, у которого все стороны различны по
длине;
Равнобедренный – треугольник, у которого две стороны равны;
Равносторонний – треугольник, у которого все стороны равны.
Равнобедренный – треугольник, у которого две стороны равны;
Равносторонний – треугольник, у которого все стороны равны.
Боковая сторона
Боковая сторона
основание
Вершина равнобедренного
треугольника
Слайд 6Свойства треугольников
Сумма углов треугольника равна 1800
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним, углов
В любом треугольнике каждая сторона меньше суммы двух других сторон
а
1
2
3
4
а
b
с
Слайд 7Прямоугольный треугольник
Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие
стороны называются катетами.
Теорема Пифагора:
Квадрат длины гипотенузы равен сумме квадратов длин катетов.
а2+b2=c2
Теорема Пифагора:
Квадрат длины гипотенузы равен сумме квадратов длин катетов.
а2+b2=c2
а
b
с
катет
катет
гипотенуза
h
h – высота, проведенная к гипотенузе
Слайд 8Свойства прямоугольного треугольника
Медиана, проведённая к гипотенузе прямоугольного треугольника, равна половине гипотенузы.
Только
в прямоугольном треугольнике центр описанной окружности лежит на стороне треугольника (совпадает с серединой гипотенузы).
а
b
с
А
В
С
О
АО=ОВ=ОС=R=0,5с
Слайд 9Признаки прямоугольных треугольников
Если квадрат одной из сторон треугольника равен сумме квадратов
двух других сторон, то такой треугольник прямоугольный.
Если медиана треугольника равна половине соответствующей ей стороны, то треугольник прямоугольный.
Если медиана треугольника равна половине соответствующей ей стороны, то треугольник прямоугольный.
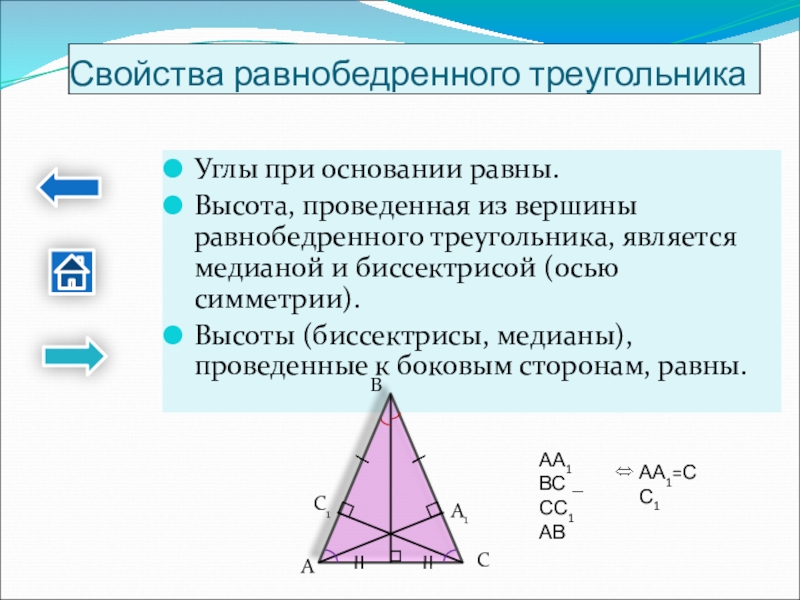
Слайд 10Свойства равнобедренного треугольника
Углы при основании равны.
Высота, проведенная из вершины равнобедренного треугольника,
является медианой и биссектрисой (осью симметрии).
Высоты (биссектрисы, медианы), проведенные к боковым сторонам, равны.
Высоты (биссектрисы, медианы), проведенные к боковым сторонам, равны.
АА1 ВС
СС1 АВ
АА1=СС1
А
В
С
А1
С1
Слайд 11Свойства правильного треугольника
Все углы равностороннего треугольника равны 60◦.
Только в правильном треугольнике
совпадают точки пересечения медиан, биссектрис, высот, серединных перпендикуляров. Эта точка называется центром правильного треугольника и является центром вписанной и описанной окружностей.
Центр правильного треугольника делит его высоты в отношении 2:1, считая от вершины.
Только в правильном треугольнике
Центр правильного треугольника делит его высоты в отношении 2:1, считая от вершины.
Только в правильном треугольнике
А
В
С
А1
С1
О
В1
АВ=ВС=АС=а
АА1=ВВ1=СС1=h
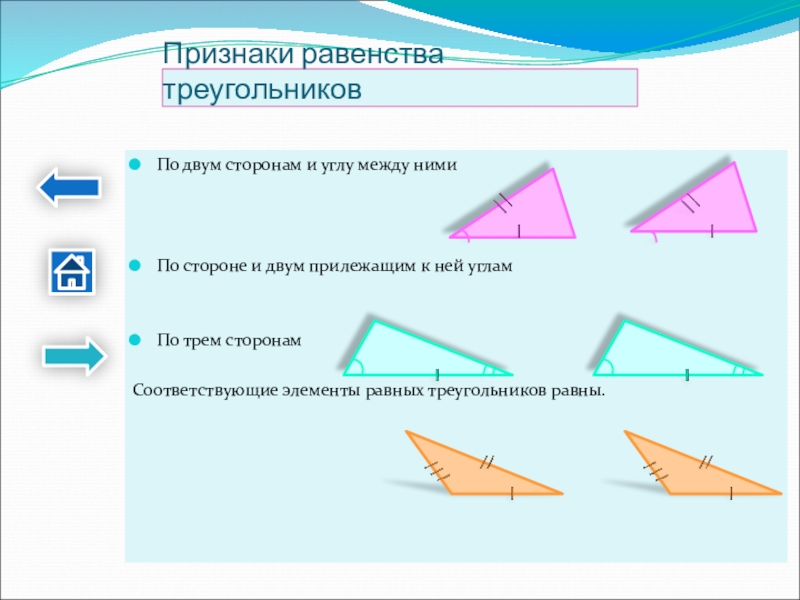
Слайд 12Признаки равенства треугольников
По двум сторонам и углу между ними
По стороне и
двум прилежащим к ней углам
По трем сторонам
Соответствующие элементы равных треугольников равны.
По трем сторонам
Соответствующие элементы равных треугольников равны.
Слайд 13Медианы
Медианы треугольника пересекаются в одной точке (центре тяжести треугольника) и делятся
этой точкой в отношении 2:1, считая от вершины.
Медиана делит треугольник на два равновеликих треугольника. Три медианы делят треугольник на шесть равновеликих треугольников.
Медиана делит треугольник на два равновеликих треугольника. Три медианы делят треугольник на шесть равновеликих треугольников.
А
В
В1
С1
АМ:МА1=ВМ:МВ1=СМ:МС1=2:1
SАС1М=SВС1М=SВА1М=SCА1М=SСВ1М=SАВ1М
АА12=
Слайд 14Биссектрисы
Все биссектрисы треугольника пересекаются в одной точке – центре вписанной в
треугольник окружности.
Биссектриса делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
Биссектриса делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника.
А
В
С
В1
А1
С1
Слайд 16Серединный перпендикуляр
Все серединные перпендикуляры сторон треугольника пересекаются в одной точке –
центре описанной около треугольника окружности. Около каждого треугольника можно описать окружность и при том только одну.
Точка пересечения серединных перпендикуляров треугольника является точкой пересечения высот треугольника, образованного средними линиями данного треугольника.
Точка пересечения серединных перпендикуляров треугольника является точкой пересечения высот треугольника, образованного средними линиями данного треугольника.
Слайд 17Площадь треугольника
S∆ = 0,5 aha= 0,5 bhb= 0,5 chc
S∆ = 0,5
ab sin C = 0,5 ac sin B = 0,5 bc sin A
S∆ = p(p-a)(p-b)(p-c) (формула Герона)
S∆ = rp
S∆ =
p=0,5(a+b+c)
r – радиус вписанной окружности
R – радиус описанной окружности
S∆ = p(p-a)(p-b)(p-c) (формула Герона)
S∆ = rp
S∆ =
p=0,5(a+b+c)
r – радиус вписанной окружности
R – радиус описанной окружности
Слайд 18Подобные треугольники
Определение.
Два треугольника называются подобными, если их углы соответственно равны и
стороны одного треугольника пропорциональны сходственным сторонам другого.
Обозначение: ∆АВС ~ ∆А1В1С1
Обозначение: ∆АВС ~ ∆А1В1С1
А
В
С
В1
А1
С1
Слайд 19Окружность,
описанная около треугольника
Около каждого треугольника можно описать окружность и при
том только одну.
Её центр – точка пересечения серединных перпендикуляров к сторонам треугольника.
Радиус (R) вычисляется по формулам:
Её центр – точка пересечения серединных перпендикуляров к сторонам треугольника.
Радиус (R) вычисляется по формулам:
А
В
С
С1
О
АВ1=В1С; АС1=С1В; ВА1=А1С
ОА ВС; ОВ АС;
ОА=ОВ=ОС=R
Слайд 20 Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
4
4
– внешний угол
Слайд 21 Медианой треугольника называется отрезок, который соединяет вершину треугольника с серединой противолежащей
стороны.
А
В
С
В1
ВВ1 – медиана треугольника
Слайд 22 Высотой треугольника называется отрезок перпендикуляра, опущенного из вершины треугольника на прямую,
содержащую противолежащую сторону.
А
В
С
СС1 - высота
Слайд 23 Биссектрисой треугольника называется отрезок биссектрисы внутреннего угла треугольника.
А
В
ВВ1 – биссектриса
Слайд 24 Средней линией треугольника называется отрезок, соединяющий середины двух сторон треугольника.
А
В
С
Р
О
РО –
средняя линия
Слайд 25 Серединным перпендикуляром называется прямая, перпендикулярная стороне треугольника и делящая её пополам.
А
В
С
В1
Слайд 26 Если в треугольниках углы равны, то стороны, лежащие против соответственно равных
углов в этих треугольниках, называются сходственными.
АВ и А1В1, ВС и В1С1, СА и С1А1 – сходственные стороны
АВ и А1В1, ВС и В1С1, СА и С1А1 – сходственные стороны
А
В
С
А1
С1
В1
Слайд 27Литература
Геометрия, 7-9: учеб. для общеобразоват. учреждений/ Л.С. Атанасян, В.Ф. Бутузов, С.Б.
Кадомцев и др. – 15-е изд.- М. : Просвещение, 2005.
Геометрия в таблицах. 7-11 кл. : Справочное пособие/ Авт.-сост. Л.И. Звавич, А.Р.Рязановский. – 5-е изд., стереотип.- М.: Дрофа, 2001.
Геометрия в таблицах. 7-11 кл. : Справочное пособие/ Авт.-сост. Л.И. Звавич, А.Р.Рязановский. – 5-е изд., стереотип.- М.: Дрофа, 2001.
