- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по геометрии на тему Признаки параллельности прямых (7 класс).
Содержание
- 1. Презентация по геометрии на тему Признаки параллельности прямых (7 класс).
- 2. Повторение.Признаки параллельности двух прямых.1)baОпределение. Две прямые
- 3. Первый признак параллельности двух прямых.bаc12
- 4. Второй признак параллельности двух прямых.
- 5. Третий признак параллельности двух прямых.Теорема.
- 6. Признаки параллельности двух прямых.Теорема. Если при
Слайд 1Признаки параллельности
двух прямых.
Задачи для школьников:
Знать формулировки признаков
2. Уметь применять признаки при
решении задач.
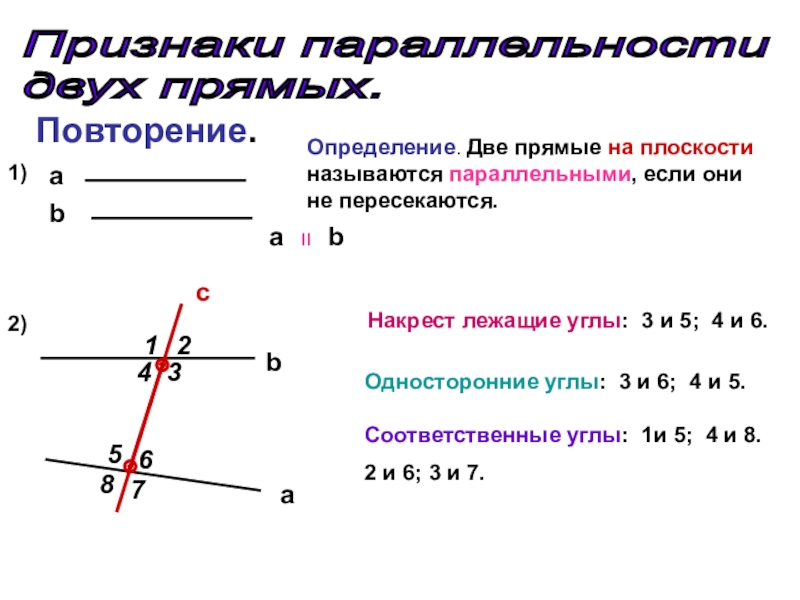
Слайд 2Повторение.
Признаки параллельности
двух прямых.
1)
b
a
Определение. Две прямые на плоскости называются параллельными, если
a
c
b
7
5
8
6
4
3
2
1
2)
Накрест лежащие углы: 3 и 5; 4 и 6.
Односторонние углы: 3 и 6; 4 и 5.
Соответственные углы: 1и 5; 4 и 8.
2 и 6; 3 и 7.
Слайд 3 Первый признак параллельности
двух прямых.
b
а
c
1
2
Теорема. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
Задача.
b
a
120о
c
120о
Докажите, что прямая а параллельна прямой b.
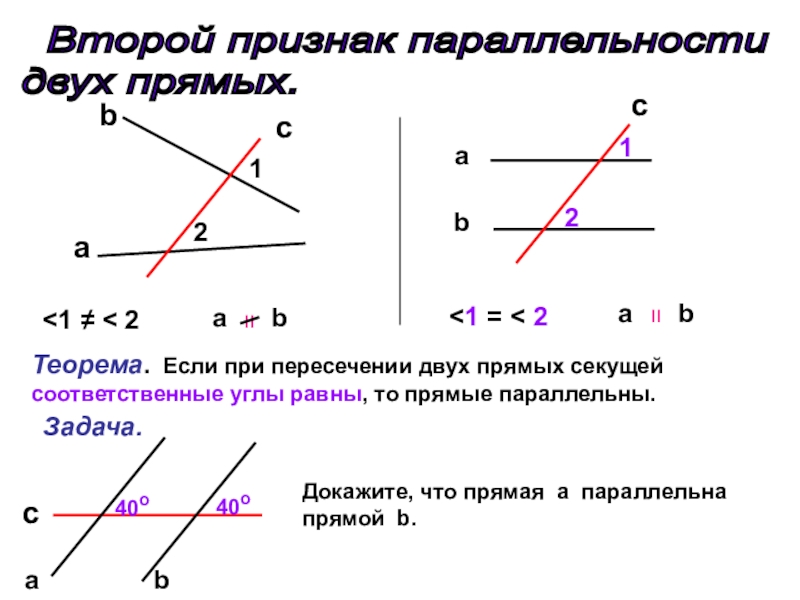
Слайд 4 Второй признак параллельности
двух прямых.
Теорема. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Задача.
b
a
c
40о
Докажите, что прямая а параллельна прямой b.
40о
Слайд 5 Третий признак параллельности
двух прямых.
Теорема. Если при пересечении двух прямых
Дано: a; b; с – секущая; < 1 и < 2 – односторонние; < 1 + < 2 = 180о
Доказать: a b
Доказательство.
1. < 1 + < 2 = 180о ( по условию)
b
a
c
1
2
3
2. < 1 и < 3 – накрест лежащие и < 1 = < 3 , значит, a b ( по первому признаку параллельности прямых).
Задача.
a
b
c
120о
60о
Докажите, что прямая а параллельна прямой b.
< 3 + < 2 = 180о ( по свойству смежных углов)
< 1 = < 3
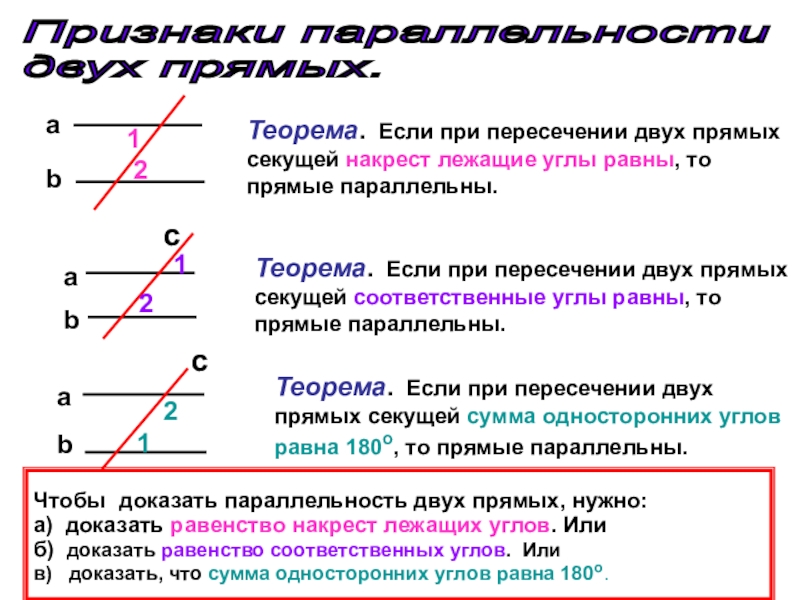
Слайд 6Признаки параллельности
двух прямых.
Теорема. Если при пересечении двух прямых секущей накрест
Теорема. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
Теорема. Если при пересечении двух прямых секущей сумма односторонних углов равна 180о, то прямые параллельны.
b
a
1
2
b
a
c
1
2
b
a
c
1
2
Чтобы доказать параллельность двух прямых, нужно:
а) доказать равенство накрест лежащих углов. Или
б) доказать равенство соответственных углов. Или
в) доказать, что сумма односторонних углов равна 180о.