- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад ук уроку геометрии на тему Симметрия, 9 класс
Содержание
- 1. Презентация ук уроку геометрии на тему Симметрия, 9 класс
- 2. Симметрия относительно плоскостиТочки А и A1 симметричны
- 3. Фигура F симметрична относительно плоскости а. Для
- 4. Куб имеет 9 плоскостей симметрии — это
- 5. Изображение любого предмета в плоском зеркале симметрично
- 6. Симметрия в пространствеа) Центральная симметрия Как
- 7. а) Центр симметрии параллелепипеда — точка пересечения его
- 8. На рисунках изображены центрально-симметричные фигуры в пространстве.
- 9. Куб имеет 9 осей симметрии — это
- 10. Прямая, проходящая через середины противоположных ребер АВ
- 11. Поверхность вращения получается вращением кривой Г вокруг
- 12. Информационные ресурсыБольшая энциклопедия Кирилла и Мефодия 2006Зенкевич И.Г. Эстетика урока математикиЯшекова Г. Математика справочник школьника
Слайд 1Презентация к уроку
учитель математики
Маркова Светлана Германовна
СИММЕТРИЯ
г. Сосновый Бор
2017 г.
Слайд 2Симметрия относительно плоскости
Точки А и A1 симметричны относительно плоскости а
Точки А
Любая точка плоскости а считается симметричной самой себе (относительно а).
Фигура называется симметричной относительно плоскости а (плоскости симметрии фигуры), если для каждой точки фигуры имеется симметричная относительно плоскости а точка этой же фигуры.
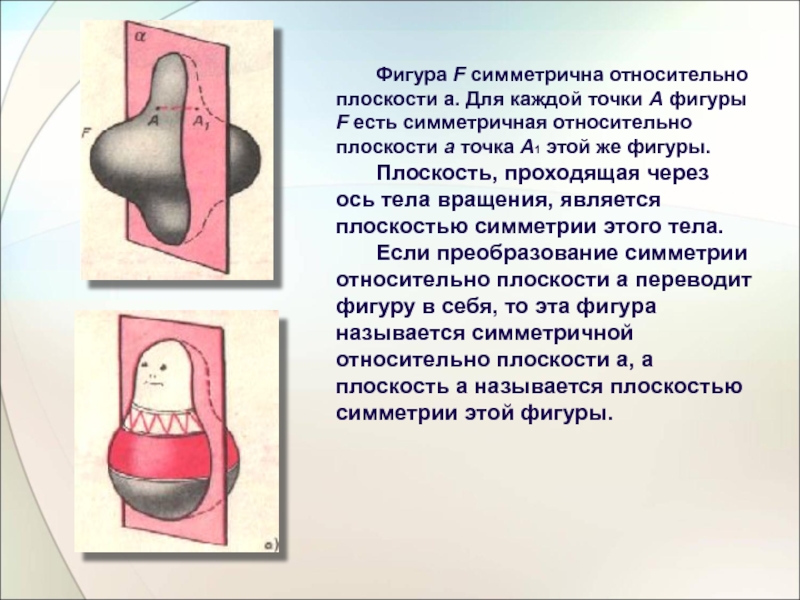
Слайд 3 Фигура F симметрична относительно плоскости а. Для каждой точки А фигуры
Плоскость, проходящая через ось тела вращения, является плоскостью симметрии этого тела.
Если преобразование симметрии относительно плоскости а переводит фигуру в себя, то эта фигура называется симметричной относительно плоскости а, а плоскость а называется плоскостью симметрии этой фигуры.
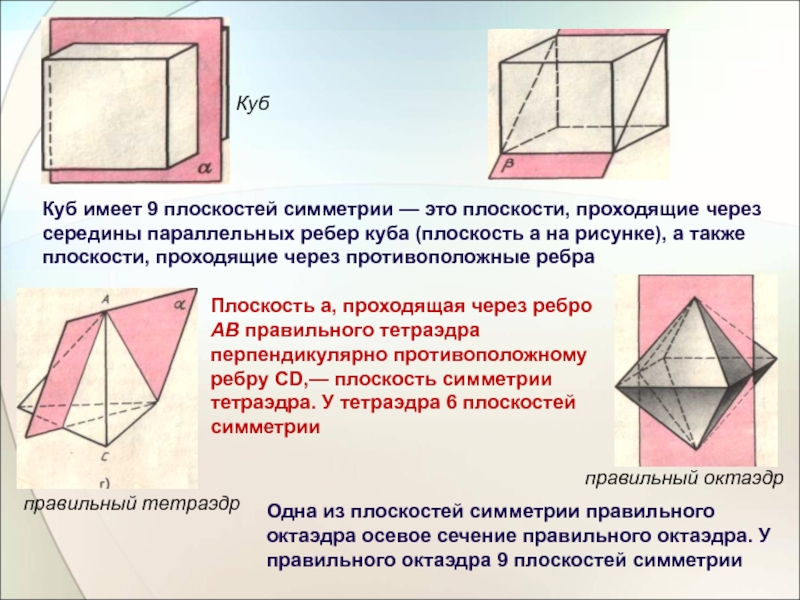
Слайд 4Куб имеет 9 плоскостей симметрии — это плоскости, проходящие через середины
Плоскость а, проходящая через ребро АВ правильного тетраэдра перпендикулярно противоположному ребру CD,— плоскость симметрии тетраэдра. У тетраэдра 6 плоскостей симметрии
Одна из плоскостей симметрии правильного октаэдра осевое сечение правильного октаэдра. У правильного октаэдра 9 плоскостей симметрии
правильный тетраэдр
Куб
правильный октаэдр
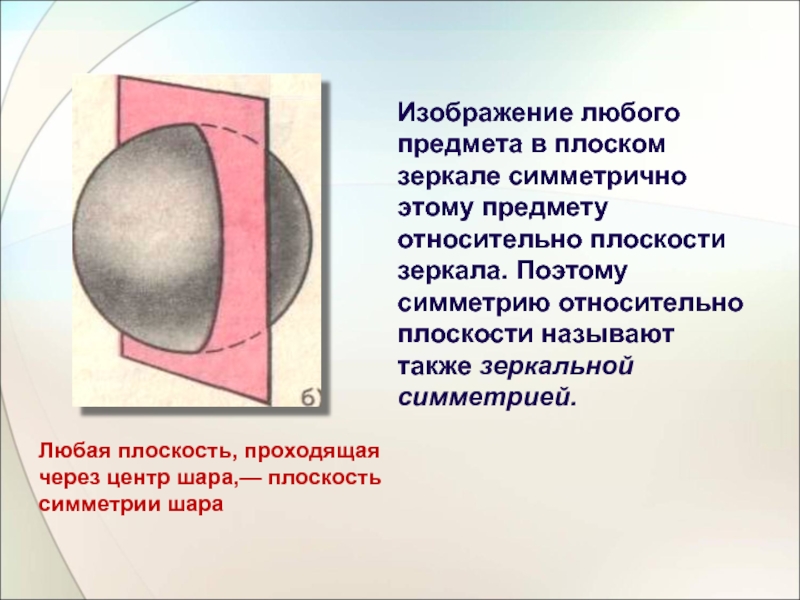
Слайд 5Изображение любого предмета в плоском зеркале симметрично этому предмету относительно плоскости
Любая плоскость, проходящая через центр шара,— плоскость симметрии шара
Слайд 6Симметрия в пространстве
а) Центральная симметрия
Как и в случае
Фигура называется симметричной относительно точки О (центра симметрии фигуры), если для каждой ее точки имеется симметричная относительно центра О точка этой же фигуры
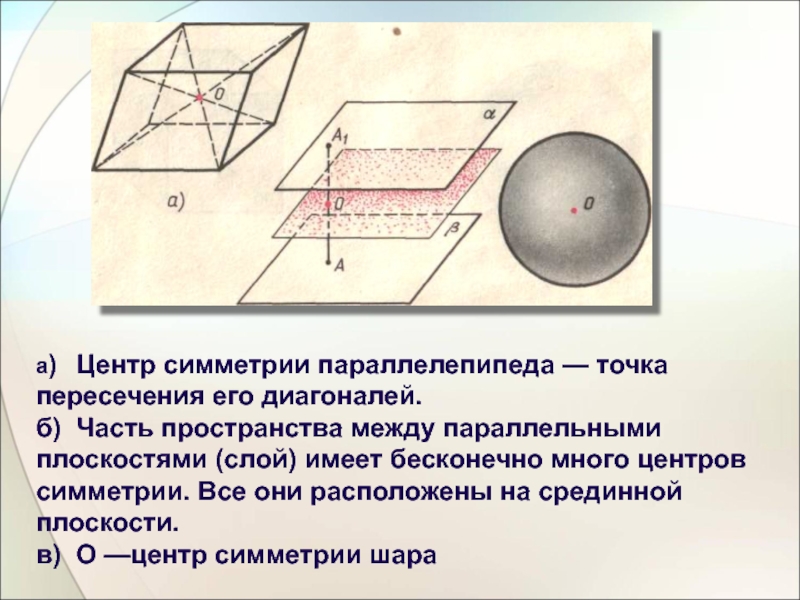
Слайд 7а) Центр симметрии параллелепипеда — точка пересечения его диагоналей.
б) Часть пространства между параллельными
в) О —центр симметрии шара
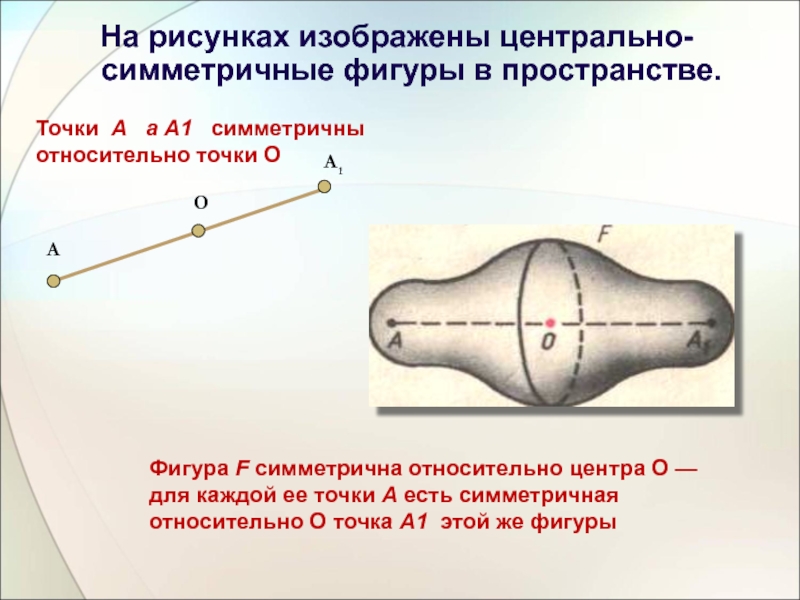
Слайд 8На рисунках изображены центрально-симметричные фигуры в пространстве.
A
O
A
1
Точки А а А1
Фигура F симметрична относительно центра О — для каждой ее точки А есть симметричная относительно О точка А1 этой же фигуры
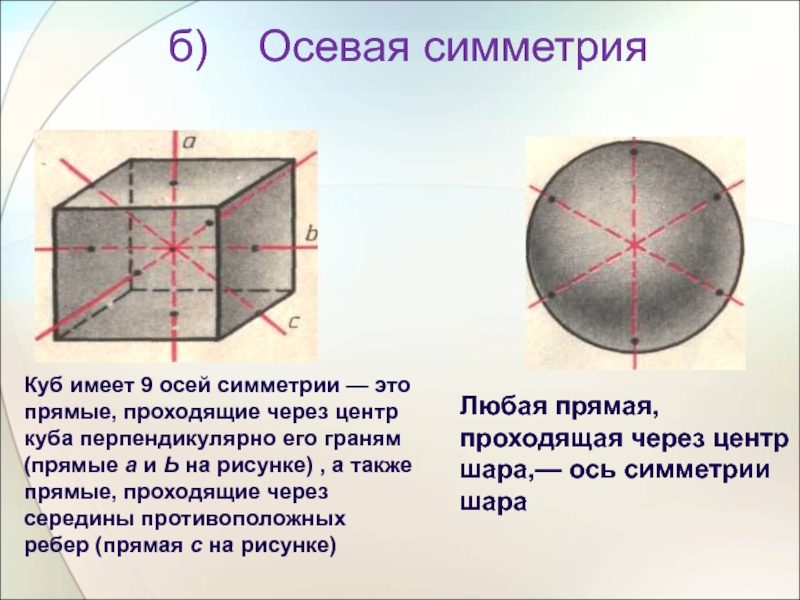
Слайд 9Куб имеет 9 осей симметрии — это прямые, проходящие через центр
б) Осевая симметрия
Любая прямая, проходящая через центр шара,— ось симметрии шара
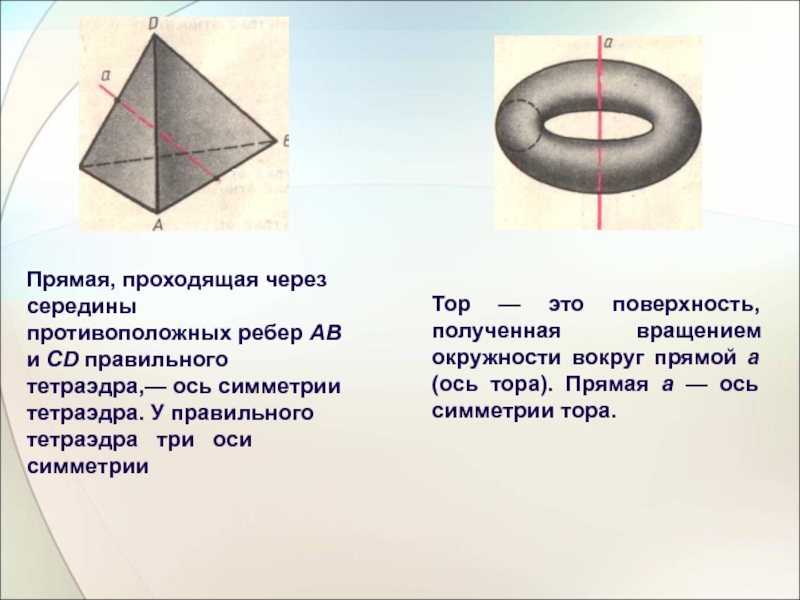
Слайд 10Прямая, проходящая через середины противоположных ребер АВ и CD правильного тетраэдра,—
Тор — это поверхность, полученная вращением окружности вокруг прямой а (ось тора). Прямая а — ось симметрии тора.
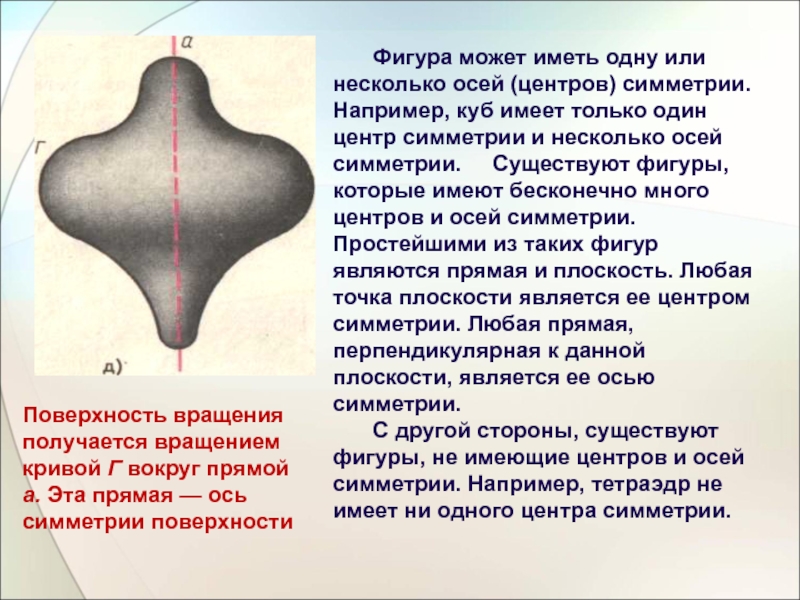
Слайд 11Поверхность вращения получается вращением кривой Г вокруг прямой а. Эта прямая
Фигура может иметь одну или несколько осей (центров) симметрии.
Например, куб имеет только один центр симметрии и несколько осей симметрии. Существуют фигуры, которые имеют бесконечно много центров и осей симметрии. Простейшими из таких фигур являются прямая и плоскость. Любая точка плоскости является ее центром симметрии. Любая прямая, перпендикулярная к данной плоскости, является ее осью симметрии.
С другой стороны, существуют фигуры, не имеющие центров и осей симметрии. Например, тетраэдр не имеет ни одного центра симметрии.