Автор работы: Митина Елизавета
8 «А» класс МБОУ СОШ № 12
города Калуги
Научный руководитель: Стоборова Э.С. Учитель математики МБОУ СОШ № 12
города Калуги
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Теорема Пифагора: от египтян до президента Америки 2 часть 8 класс
Содержание
- 1. Презентация Теорема Пифагора: от египтян до президента Америки 2 часть 8 класс
- 2. Предмет исследования: Прикладное значение теоремы Пифагора
- 3. Слайд 3
- 4. 1) Практическое применение теоремы Пифагора в
- 5. 2) Задача Бхаскари «На берегу реки рос
- 6. 3) Задача из китайской «Математики в девяти
- 7. 4) Задача из учебника «Арифметика» Леонтия Магницкого
- 8. 5) Теорема Пифагора в строительстве и архитектуре
- 9. При строительстве домов и коттеджей
- 10. Практическое применение
- 11. Пифагоровы тройки.Пифагоровы тройки могут быть: примитивными
- 12. ЗАКЛЮЧЕНИЕ :Мы пришли к главному выводу: теорема
Слайд 1 Теорема Пифагора:
Слайд 3
Прикладное значение теоремы Пифагора:
Теорема
Слайд 4
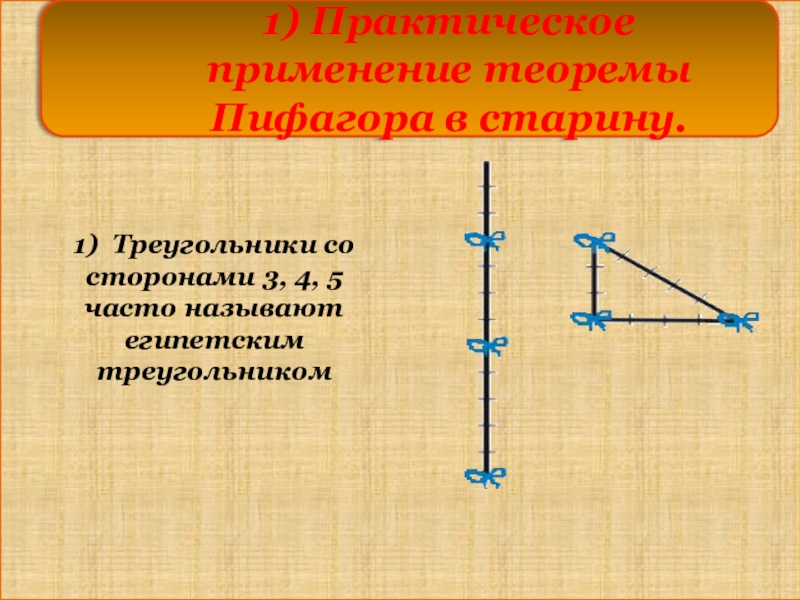
1) Практическое применение теоремы Пифагора в старину.
1) Треугольники со сторонами
Слайд 52) Задача Бхаскари
«На берегу реки рос тополь одинокий.
Вдруг
АВ2 = ВС2 + АС2 = 9 +16 = 25, АВ = = 5 (футов); СD = 3 + 5 = 8 (футов).
Слайд 63) Задача из китайской «Математики в девяти книгах»
Имеется водоем
(x+1)2 =x2 + 25, где х – глубина воды; 2x= 24; x=12 (чи); тогда х + 1 = 12+1= 13 (чи) – длина камыша.
Слайд 74) Задача из учебника «Арифметика» Леонтия Магницкого
Случися некому человеку
ВС2 = АВ2 – АС2 = 15625 – 13689 = 1936; ВС = 44 (стоп)
Слайд 85) Теорема Пифагора в строительстве и архитектуре – окно.
Окно в романской
Окно готического стиля
Слайд 9
При строительстве домов
и коттеджей часто встает
вопрос
если уже изготовлены балки.
Этот вопрос встал и перед
моим папой 2 года назад: на даче
задумано построить двускатную
крышу (форма в сечении).
Какой длины должны быть
стропила, если изготовлены балки
AС = 10 м и BH = 2,5 м.
АВ2 = АН2 + ВН2
значит, AB2 = 52 + 2,52 = 25 + 6,25 = 31,25 (м2)
AH ≈ 5,6 м
6) Папина задача – строительство
дачной крыши.
Слайд 10 Практическое применение
теоремы Пифагора.
С помощью теоремы можно вычислить длину стропила
для двускатной крыши. Определить, какой высоты
вышка мобильной связи нужна, чтобы сигнал достигал
определенного населенного пункта. И даже устойчиво
установить новогоднюю елку на городской площади.
Как видите, эта теорема живет не только на страницах
учебников, но и часто бывает полезна в реальной жизни.
Слайд 11
Пифагоровы тройки.
Пифагоровы тройки могут быть:
примитивными (все три числа –
не примитивными (если каждое число тройки
умножить на одно и то же число, получится новая
тройка, которая не является примитивной).
Примеры Пифагоровых троек:
(3, 4, 5), (6, 8, 10), (5, 12, 13), (9, 12, 15), (8, 15, 17),
(12, 16, 20),(15, 20, 25), (7, 24, 25), (10, 24, 26),
(20, 21, 29) и т.д.