МБОУ «Гимназия №4 им. А.С. Пушкина»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Теорема Менелая в тетраэдрах -подготовка к ЕГЭ по математике №14 (стереометрическая задача)
Содержание
- 1. Презентация Теорема Менелая в тетраэдрах -подготовка к ЕГЭ по математике №14 (стереометрическая задача)
- 2. Задачи: 1. показать применение теоремы Менелая к
- 3. Теорема МенелаяЕсли на сторонах АВ и ВС
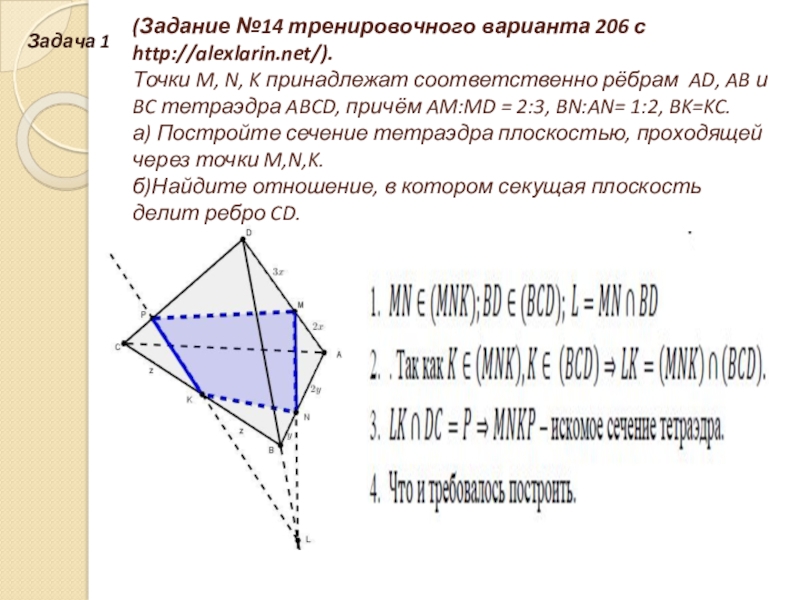
- 4. (Задание №14 тренировочного варианта 206 с http://alexlarin.net/).
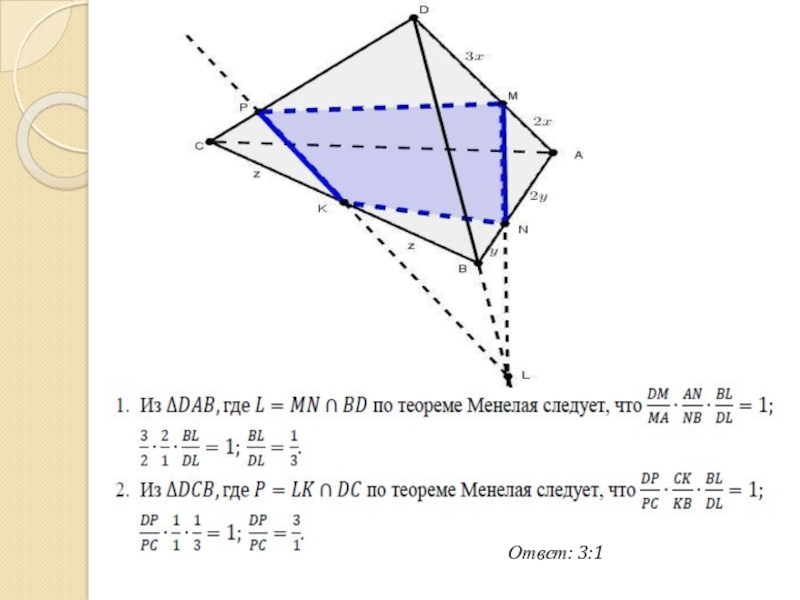
- 5. Ответ: 3:1
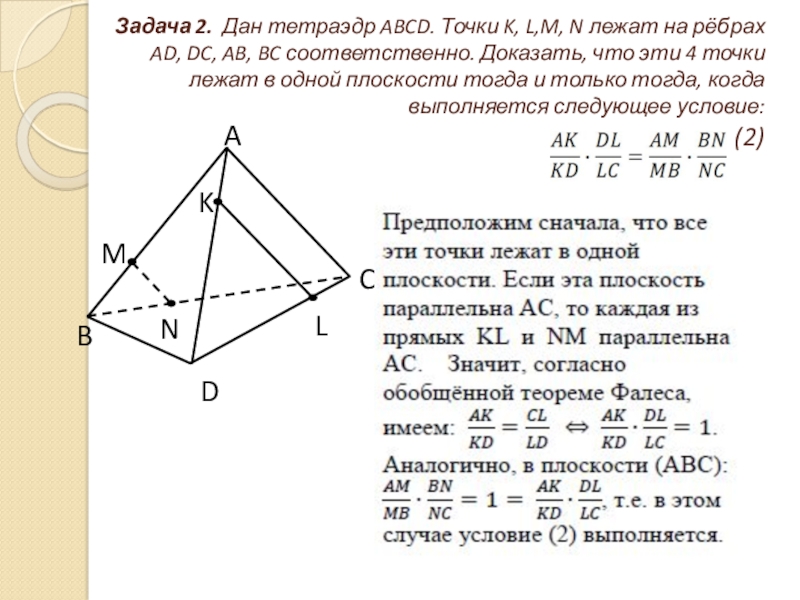
- 6. Задача 2. Дан тетраэдр
- 7. Слайд 7
- 8. Слайд 8
- 9. Вспомогательная задача (*)Три прямые пересекаются в точке
- 10. Дан тетраэдр ABCD. Точки K, L и
- 11. Благодарю за внимание
Задачи: 1. показать применение теоремы Менелая к тетраэдрам; 2. развить стереометрическое мышление на более высоком уровне; 3. помочь учителю оценить свой потенциал с точки зрения образовательной перспективы; 4. способствовать интеллектуальному развитию учителя, формированию качеств мышления,
Слайд 1Теорема Менелая в тетраэдрах
Учитель математики
высшей квалификационной категории:
Софина Надежда Юрьевна
ноябрь
2017
Слайд 2Задачи: 1. показать применение теоремы Менелая к тетраэдрам; 2. развить стереометрическое мышление
на более высоком уровне;
3. помочь учителю оценить свой потенциал с точки зрения образовательной перспективы;
4. способствовать интеллектуальному развитию учителя, формированию качеств мышления, характерных для математической деятельности.
ЦЕЛЬ: помочь учителю-предметнику в организации подготовки старшеклассников к успешному решению экзаменационных стереометрических задач
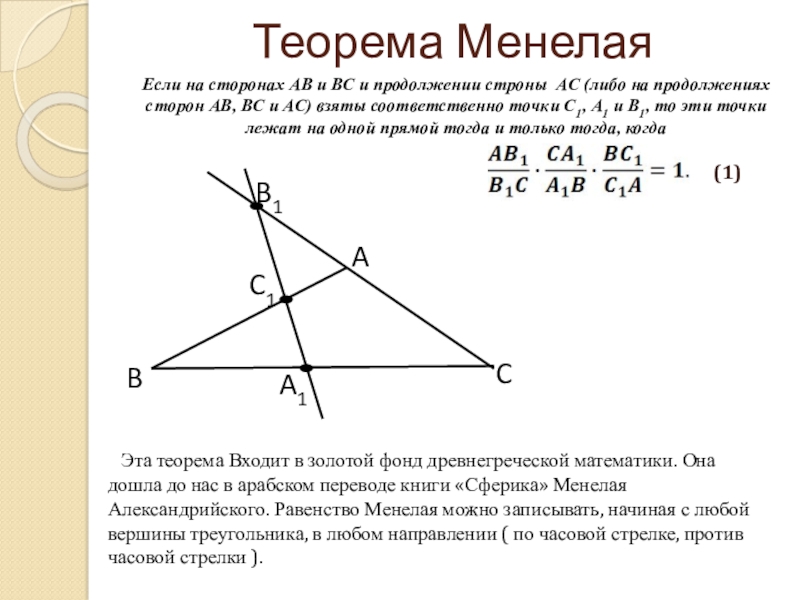
Слайд 3Теорема Менелая
Если на сторонах АВ и ВС и продолжении строны АС
(либо на продолжениях сторон АВ, ВС и АС) взяты соответственно точки С1, А1 и В1, то эти точки лежат на одной прямой тогда и только тогда, когда
Эта теорема Входит в золотой фонд древнегреческой математики. Она дошла до нас в арабском переводе книги «Сферика» Менелая Александрийского. Равенство Менелая можно записывать, начиная с любой вершины треугольника, в любом направлении ( по часовой стрелке, против часовой стрелки ).
(1)
Слайд 4(Задание №14 тренировочного варианта 206 с http://alexlarin.net/). Точки M, N, K принадлежат
соответственно рёбрам AD, AB и BC тетраэдра ABCD, причём AM:MD = 2:3, BN:AN= 1:2, BK=KC.
а) Постройте сечение тетраэдра плоскостью, проходящей через точки M,N,K.
б)Найдите отношение, в котором секущая плоскость делит ребро CD.
Задача 1
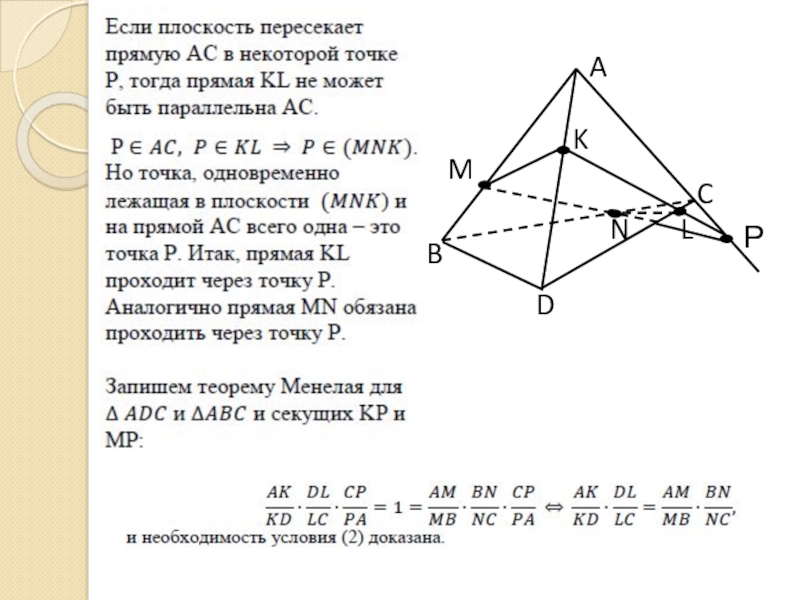
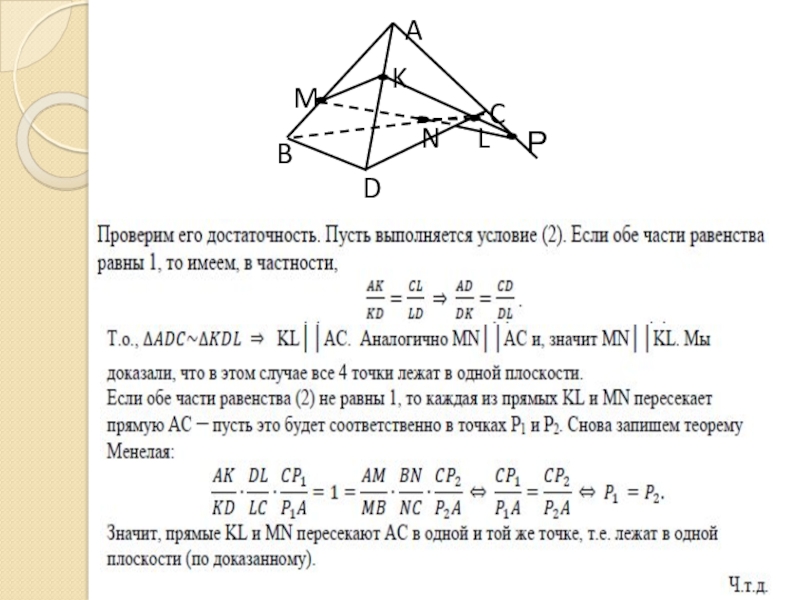
Слайд 6 Задача 2. Дан тетраэдр ABCD. Точки K, L,M, N лежат
на рёбрах AD, DC, AB, BC соответственно. Доказать, что эти 4 точки лежат в одной плоскости тогда и только тогда, когда выполняется следующее условие:
(2)
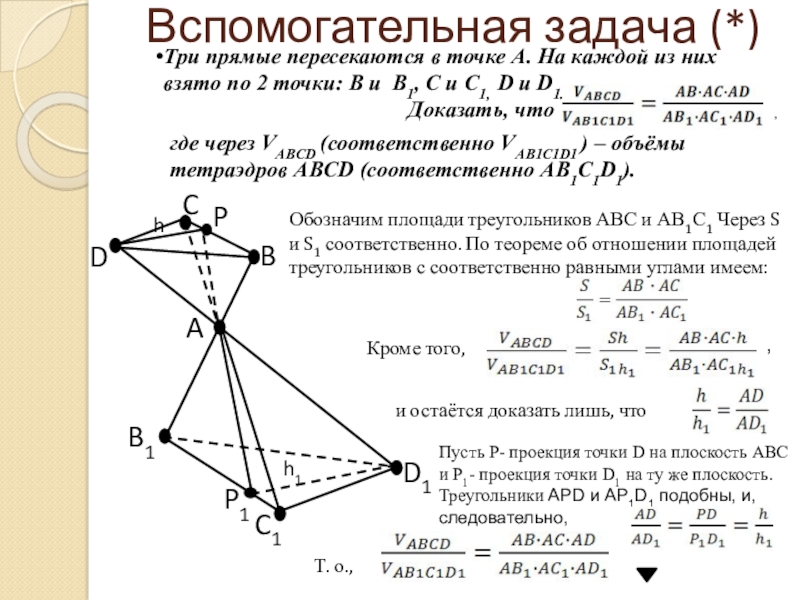
Слайд 9Вспомогательная задача (*)
Три прямые пересекаются в точке А. На каждой из
них взято по 2 точки: В и В1, С и С1, D и D1.
Доказать, что
Доказать, что
где через VABCD (соответственно VAB1C1D1 ) – объёмы тетраэдров ABCD (соответственно AB1C1D1).
,
Обозначим площади треугольников АВС и АВ1С1 Через S и S1 соответственно. По теореме об отношении площадей треугольников с соответственно равными углами имеем:
Кроме того,
и остаётся доказать лишь, что
Пусть Р- проекция точки D на плоскость АВС и Р1- проекция точки D1 на ту же плоскость. Треугольники АPD и АP1D1 подобны, и, следовательно,
,
Т. о.,
.
,
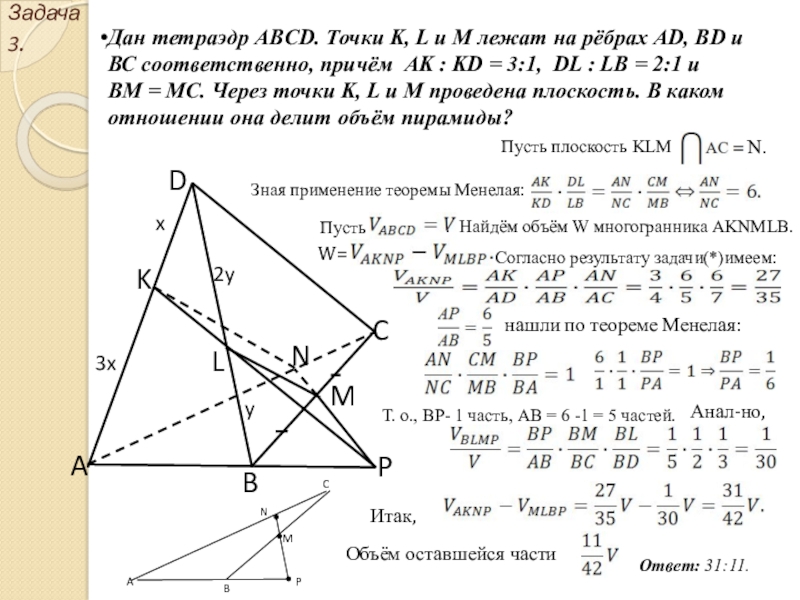
Слайд 10Дан тетраэдр ABCD. Точки K, L и M лежат на рёбрах
AD, BD и ВС соответственно, причём AK : KD = 3:1, DL : LB = 2:1 и
ВМ = МС. Через точки K, L и M проведена плоскость. В каком отношении она делит объём пирамиды?
ВМ = МС. Через точки K, L и M проведена плоскость. В каком отношении она делит объём пирамиды?
Задача 3.
Пусть плоскость KLM
Зная применение теоремы Менелая:
Пусть
. Найдём объём W многогранника AKNMLB.
W=
Согласно результату задачи(*)имеем:
нашли по теореме Менелая:
Т. о., ВР- 1 часть, АВ = 6 -1 = 5 частей.
Анал-но,
Итак,
Объём оставшейся части
Ответ: 31:11.
N.
