по геометрии для 8 класса
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад на тему Гл. 3. Урок 11. Пропорциональные отрезки
Содержание
- 1. Гл. 3. Урок 11. Пропорциональные отрезки
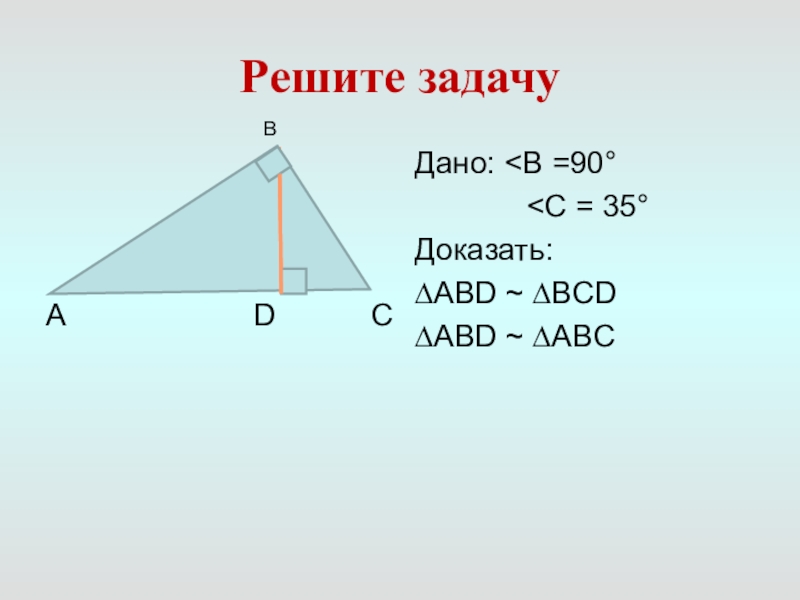
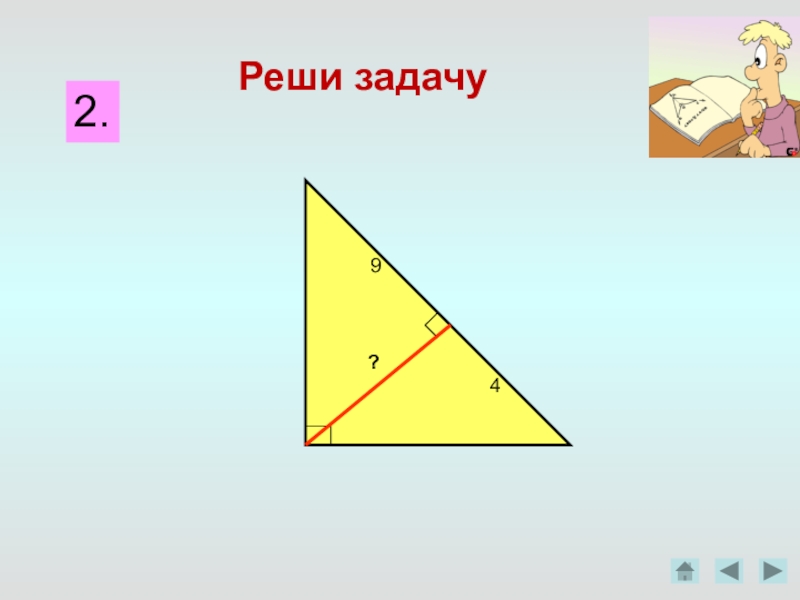
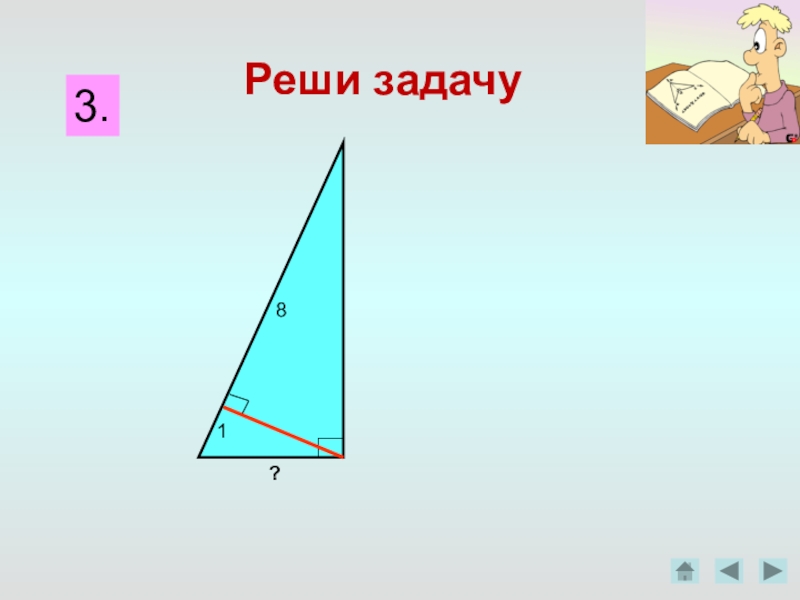
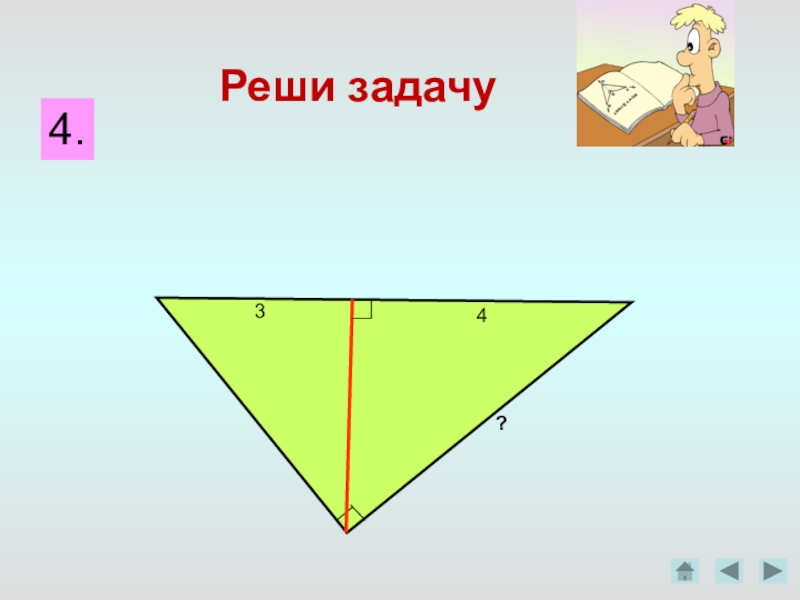
- 2. Решите задачу
- 3. ЗАДАНИЕ №1ABCA1B1C1350550a) Подобны ли Δ ABC и
- 4. Определение Отрезок XY называется средним пропорциональным
- 5. Решите задачу №1. Найдите длину среднего пропорционального
- 6. Решите задачу № 2. Найдите длину отрезка
- 7. ACBD?1. ∟ADС= ∟CDB (т.к. СD-высота)2. ∟СAD= ∟BCD
- 8. Дано:Δ ABС – прямоугольный∟С- прямойCD - высотаДоказать:1.
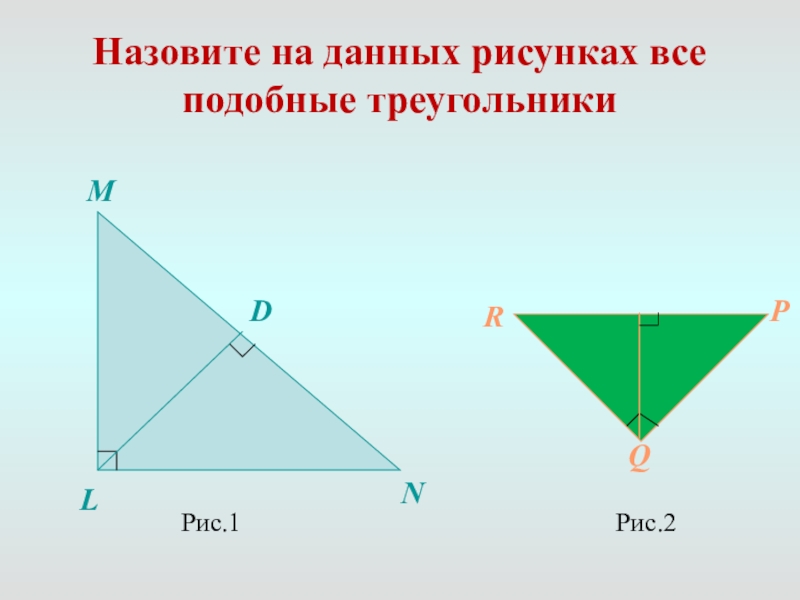
- 9. Назовите на данных рисунках все подобные треугольникиРис.1Рис.2LMNDRPQ
- 10. Δ ACD~ ΔCBDопр. подобиясв-во пропорцииВывод: высота прямоугольного
- 11. Докажите, что катет прямоугольного треугольника есть среднее
- 12. Свойство 1. Высота прямоугольного треугольника, проведённая из
- 13. ·
- 14. Слайд 14
- 15. Слайд 15
- 16. Слайд 16
- 17. Решить задачи № 572 (б), 574 (а)
- 18. Домашнее заданиеЧитать п.63Отвечать на вопросы 10-11.Решить №№ 572 (а, в, д), 574 (б), 573
Решите задачу A D СДано:
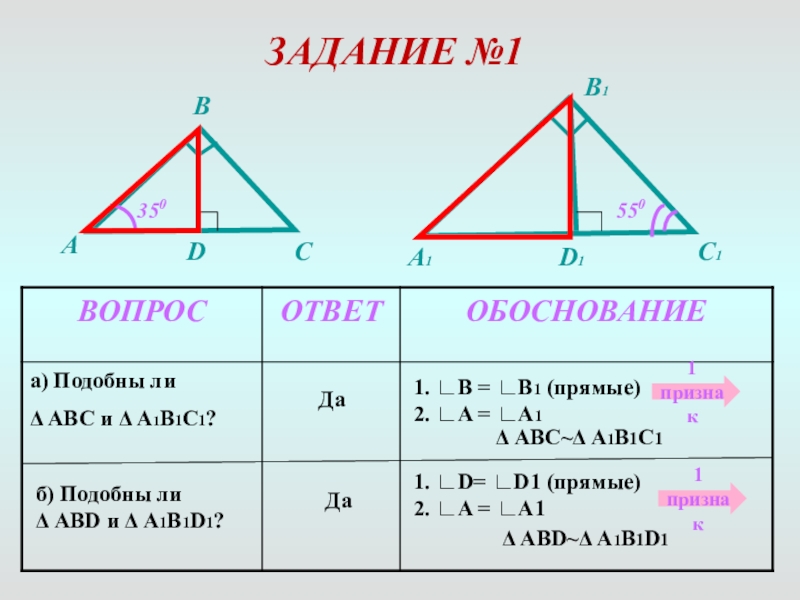
Слайд 3ЗАДАНИЕ №1
A
B
C
A1
B1
C1
350
550
a) Подобны ли
Δ ABC и Δ A1B1C1?
1 признак
Δ ABC~Δ
A1B1C1
б) Подобны ли Δ ABD и Δ A1B1D1?
Да
Да
1. ∟В = ∟В1 (прямые)
2. ∟A = ∟А1
D
D1
1. ∟D= ∟D1 (прямые)
2. ∟A = ∟A1
1 признак
Δ ABD~Δ A1B1D1
Слайд 4Определение
Отрезок XY называется средним пропорциональным (или средним геометрическим) между
отрезками AB и CD, если выполняется равенство:
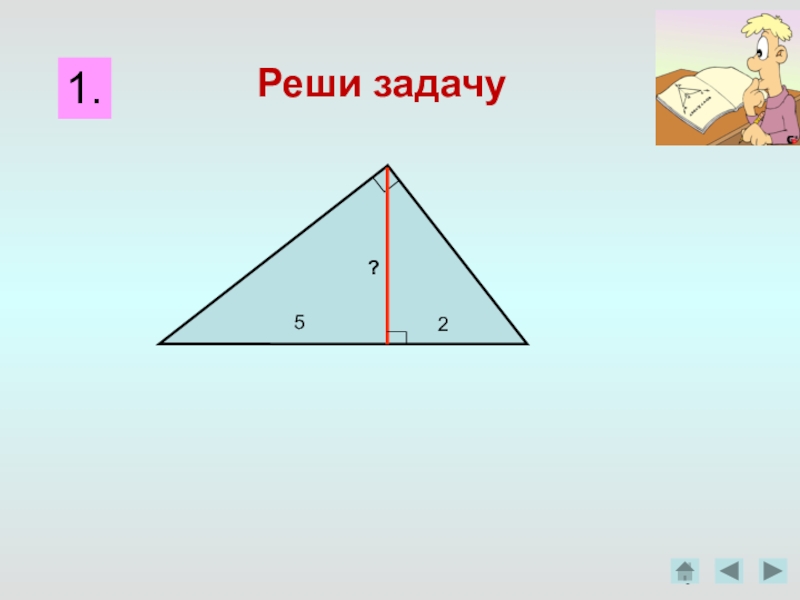
Слайд 5Решите задачу
№1. Найдите длину среднего пропорционального отрезков MN и KP,
если MN = 9см, KP = 16см
XY = 3∙4 = 12 (см)
Слайд 6Решите задачу
№ 2. Найдите длину отрезка AB, если среднее пропорциональное
отрезков AB и СD равно 90 см и CD = 100 см
Слайд 7
A
C
B
D
?
1. ∟ADС= ∟CDB (т.к. СD-высота)
2. ∟СAD= ∟BCD (т.к. Δ BDC~Δ ABC)
1
признак
Δ ADB~Δ CDB
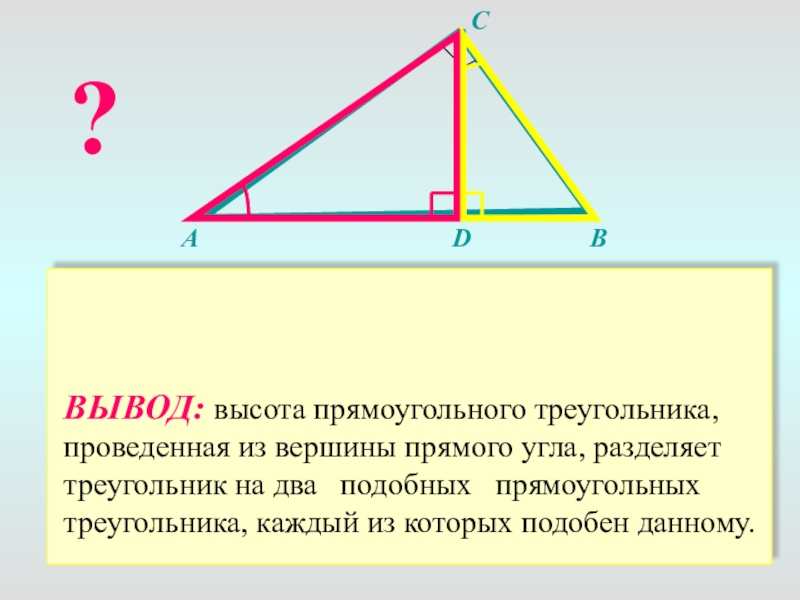
ВЫВОД: высота прямоугольного треугольника, проведенная из вершины прямого угла, разделяет треугольник на два подобных прямоугольных треугольника, каждый из которых подобен данному.
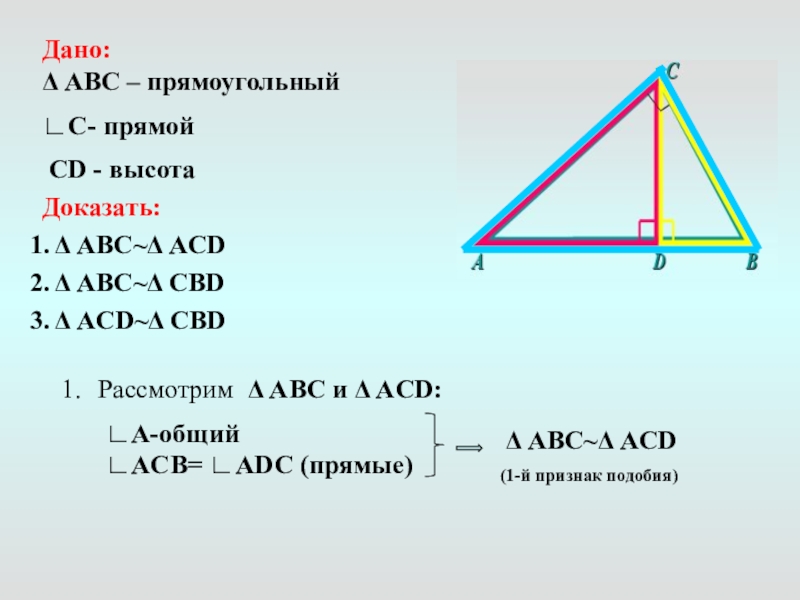
Слайд 8Дано:
Δ ABС – прямоугольный
∟С- прямой
CD - высота
Доказать:
1. Δ ABС~Δ AСD
2. Δ
ABС~Δ CBD
3. Δ ACD~Δ CBD
Рассмотрим Δ ABС и Δ AСD:
∟A-общий
∟ACB= ∟ADC (прямые)
Δ ABС~Δ AСD
(1-й признак подобия)
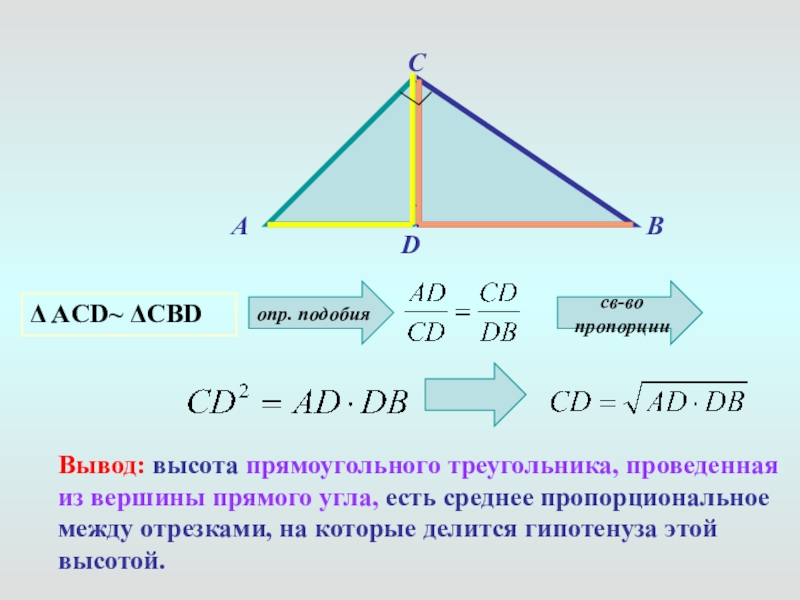
Слайд 10Δ ACD~ ΔCBD
опр. подобия
св-во пропорции
Вывод: высота прямоугольного треугольника, проведенная из вершины
прямого угла, есть среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
A
C
B
D
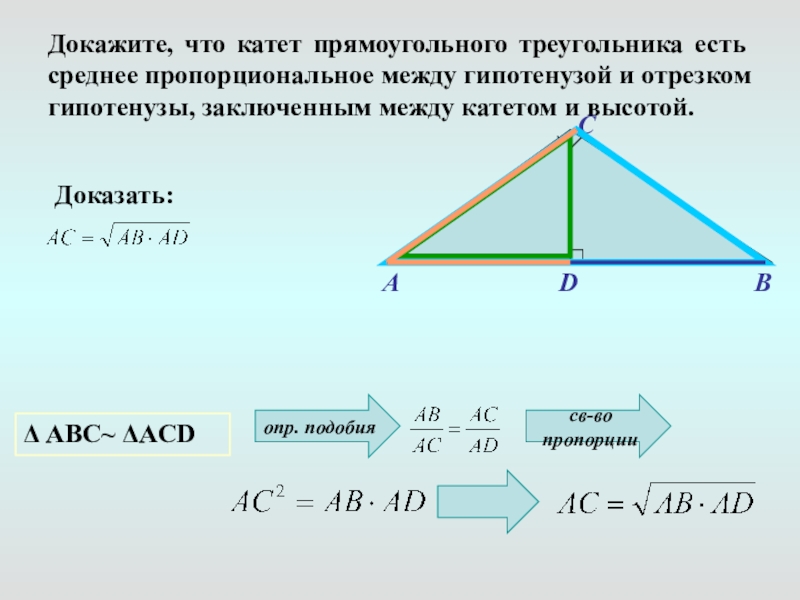
Слайд 11Докажите, что катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и
отрезком гипотенузы, заключенным между катетом и высотой.
Δ AВС~ ΔACD
св-во пропорции
Доказать:
опр. подобия
A
С
B
D
Слайд 12Свойство 1.
Высота прямоугольного треугольника, проведённая из вершины прямого угла, есть
среднее пропорциональное между отрезками, на которые делится гипотенуза этой высотой.
Свойство 2.
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключённым между катетом и высотой,
проведённой из вершины прямого угла.
Свойство 2.
Катет прямоугольного треугольника есть среднее пропорциональное между гипотенузой и отрезком гипотенузы, заключённым между катетом и высотой,
проведённой из вершины прямого угла.
