- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Свойства равнобедренного треугольника
Содержание
- 1. Презентация Свойства равнобедренного треугольника
- 2. Отрезок, соединяющий любую вершину треугольника с
- 3. Отрезок, соединяющий любую вершину треугольника с
- 4. Укажите, какой элемент (выделен цветом) изображен на каждом из рисунковбиссектрисавысотамедиана
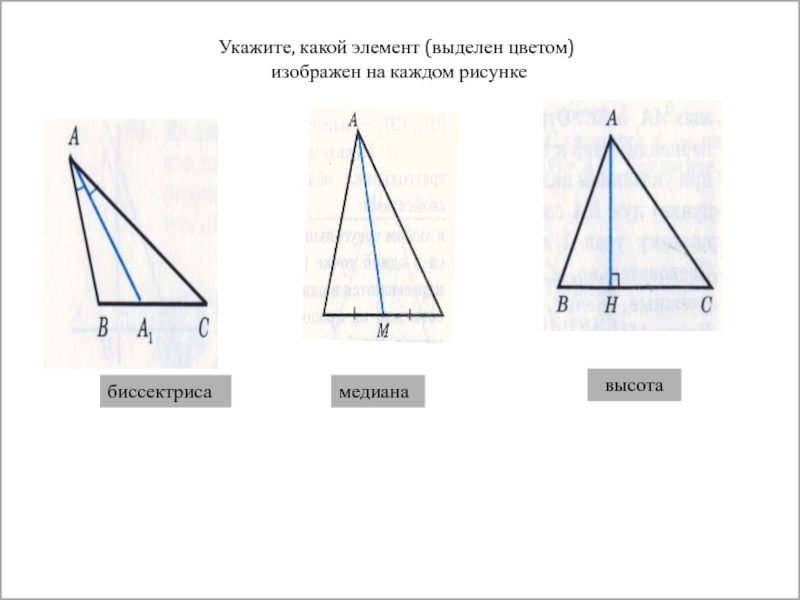
- 5. Укажите, какой элемент (выделен цветом) изображен на каждом рисункебиссектрисавысотамедиана
- 6. В любом треугольнике медианы пересекаются в одной
- 7. Полезно знать! Треугольник по праву
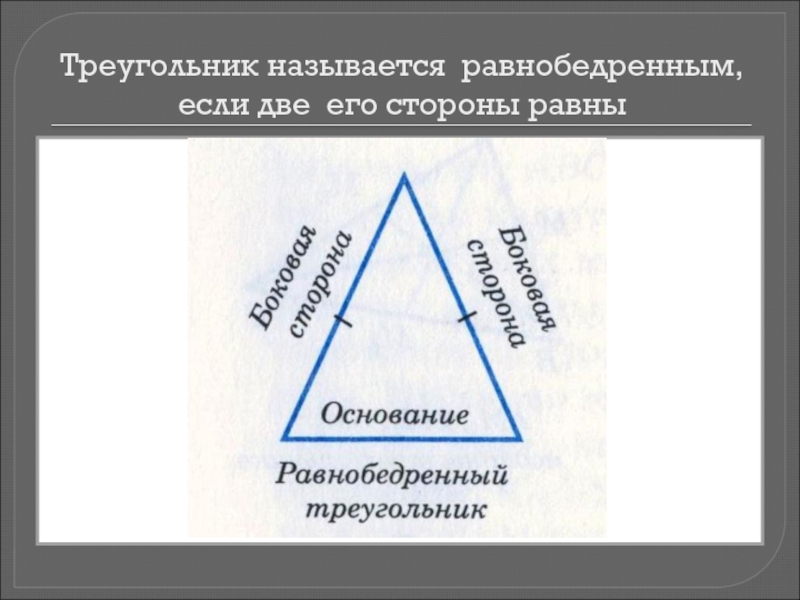
- 8. Треугольник называется равнобедренным, если две его стороны равны
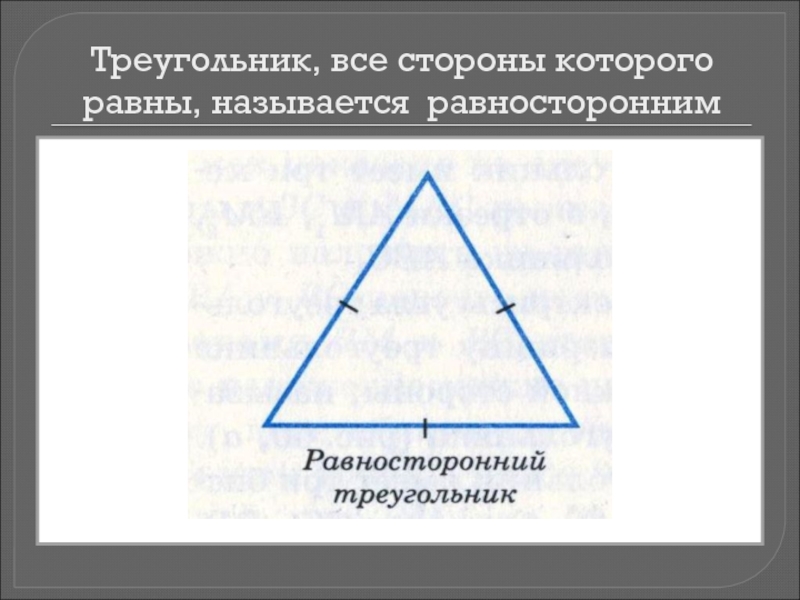
- 9. Треугольник, все стороны которого равны, называется равносторонним
- 10. Т. В равнобедренном треугольнике углы при основании
- 11. Т. В равнобедренном треугольнике биссектриса проведенная к
- 12. Т. В равнобедренном треугольнике биссектриса проведенная к
- 13. Мы установили, что биссектриса, медиана
- 14. Начертите треугольник.С помощью транспортира и линейки проведите его биссектрисы.Задача
- 15. В равнобедренном треугольнике боковая сторона в
- 16. В равнобедренном треугольнике боковая сторона в
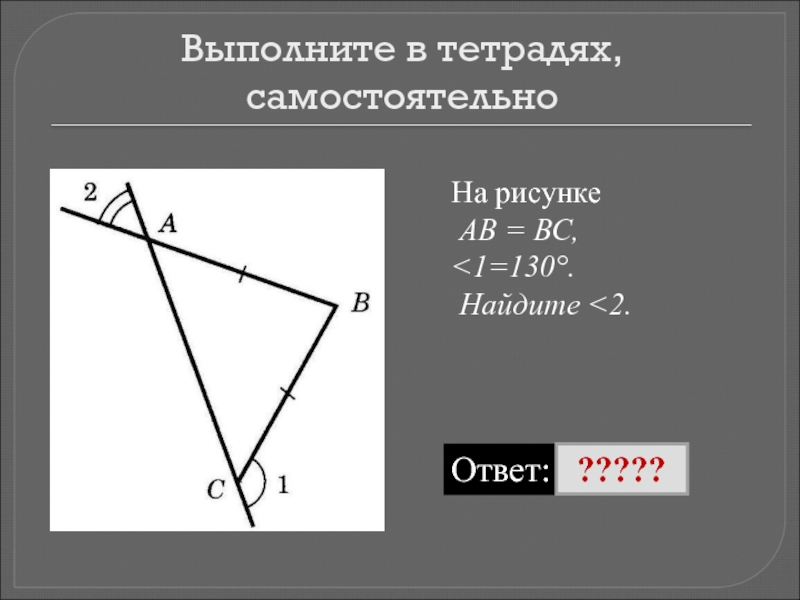
- 17. Выполните в тетрадях, самостоятельноНа рисунке АВ = ВС,
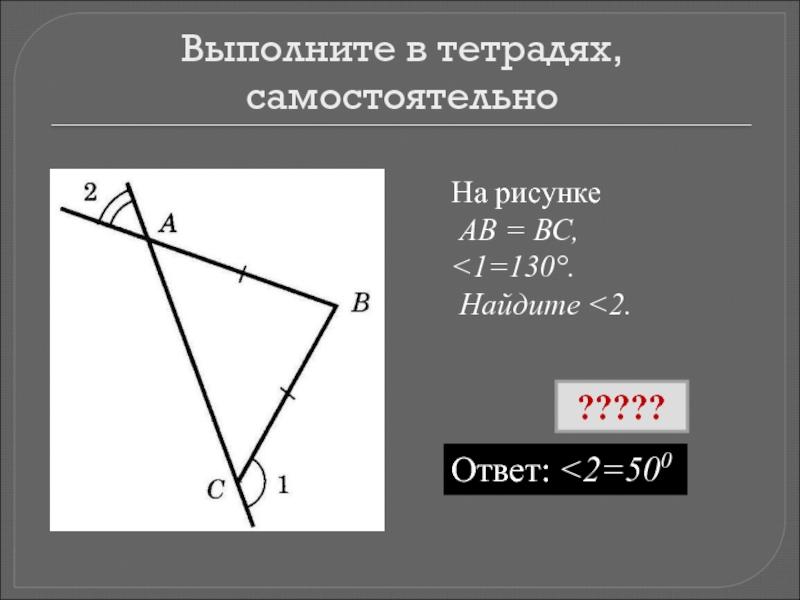
- 18. Выполните в тетрадях, самостоятельноНа рисунке АВ = ВС,
- 19. Логическая задачаВозьмите из коробка шесть обыкновенных спичек и попытайтесь составить из них четыре равносторонних треугольника.Решение здесь!!!
- 20. Логическая задачаВозьмите из коробка шесть обыкновенных спичек и попытайтесь составить из них четыре равносторонних треугольника.Решение здесь!!!
- 21. Домашнее задание№ 117Знать формулировки теорем, уметь доказывать их.
- 22. http://www.bymath.net/studyguide/geo/sec/geo7.htmhttp://ru.wikipedia.org/wiki/Равнобедренный_ треугольник http://neive.by.ru/geometriia/treug/rbrstr.htmlhttp://iljazhe.f5.ru/post/252551 Геометрия 7-9. Л.С. Атанасян,
Слайд 1Свойства равнобедренного треугольника.
Цель урока:
Повторить материал: «Медианы, высоты, биссектрисы треугольника»
Изучить теоретический материал:
Закрепить навыки работы учащихся с интерактивной доской»
Слайд 2 Отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны называется
Перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону или её продолжение называется высотой треугольника.
Отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной называется
биссектрисой треугольника.
Слайд 3 Отрезок, соединяющий любую вершину треугольника с серединой противоположной стороны называется
Перпендикуляр, опущенный из любой вершины треугольника на противоположную сторону или её продолжение называется высотой треугольника.
Отрезок биссектрисы угла от вершины до точки пересечения с противоположной стороной называется
биссектрисой треугольника.
Слайд 4
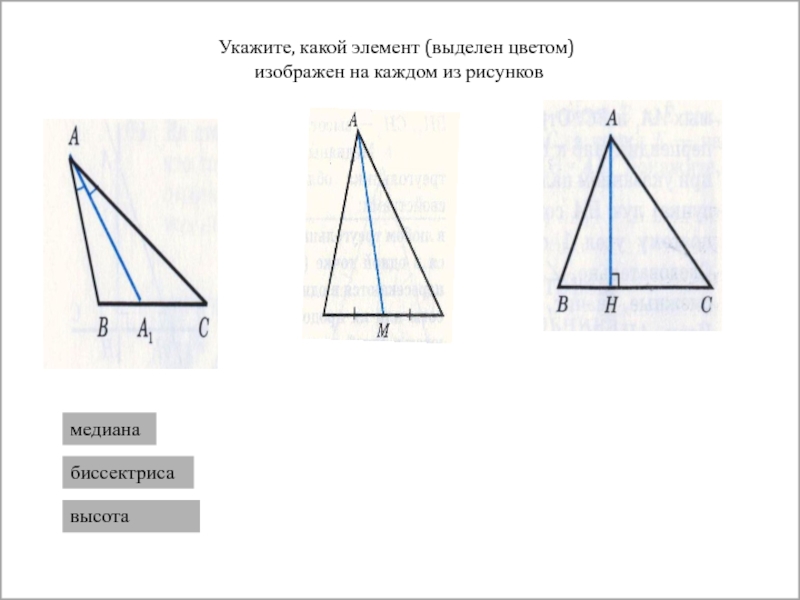
Укажите, какой элемент (выделен цветом)
изображен на каждом из рисунков
биссектриса
высота
медиана
Слайд 6
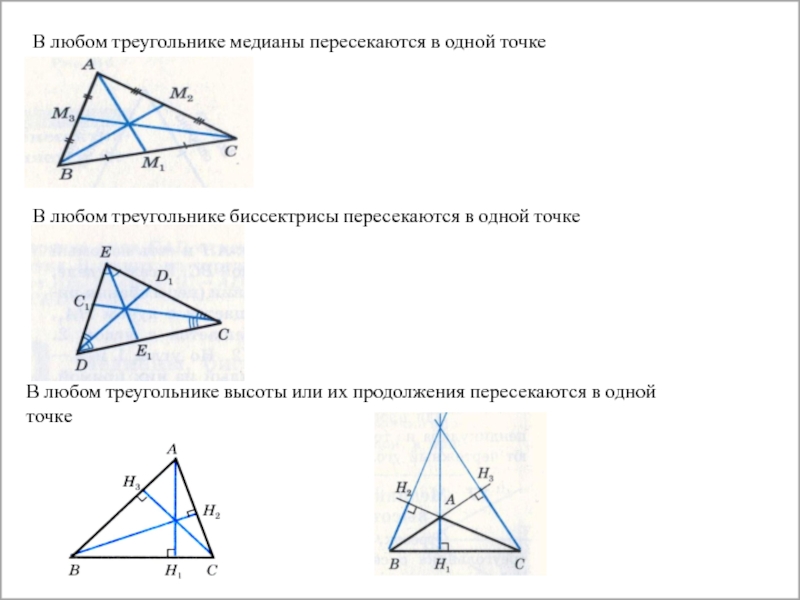
В любом треугольнике медианы пересекаются в одной точке
В любом треугольнике биссектрисы
В любом треугольнике высоты или их продолжения пересекаются в одной точке
Слайд 7Полезно знать!
Треугольник по праву считается простейшей из фигур:
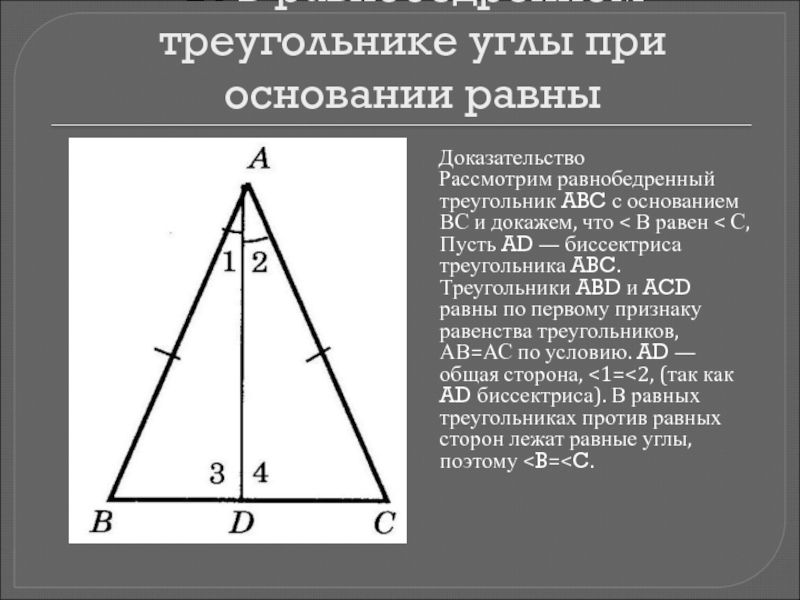
Слайд 10Т. В равнобедренном треугольнике углы при основании равны
Доказательство
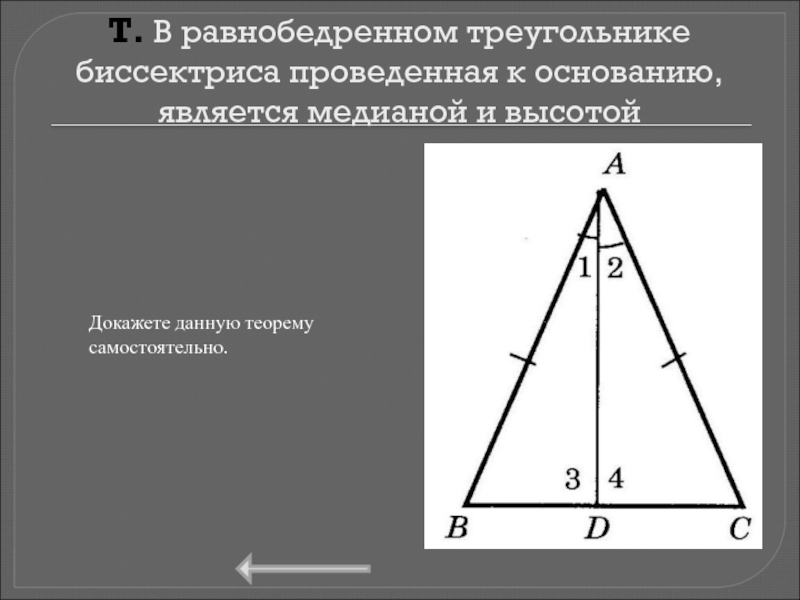
Слайд 11Т. В равнобедренном треугольнике биссектриса проведенная к основанию, является медианой и
Доказательство
Обратимся к рисунку, на котором ABC — равнобедренный треугольник с основанием ВС, AD — его биссектриса.
Из равенства треугольников ABD и ACD следует, что BD=DC и <3=<4. Равенство BD = DC означает, что точка D— середина стороны ВС и поэтому AD — медиана треугольника ABC. Так как углы 3 и 4 — смежные и равны друг другу, то они прямые. Следовательно, отрезок AD является также высотой треугольника ABC.
Теорема доказана.
Докажете данную теорему
самостоятельно.
Слайд 12Т. В равнобедренном треугольнике биссектриса проведенная к основанию, является медианой и
Доказательство
Обратимся к рисунку, на котором ABC — равнобедренный треугольник с основанием ВС, AD — его биссектриса.
Из равенства треугольников ABD и ACD следует, что BD=DC и <3=<4. Равенство BD = DC означает, что точка D— середина стороны ВС и поэтому AD — медиана треугольника ABC. Так как углы 3 и 4 — смежные и равны друг другу, то они прямые. Следовательно, отрезок AD является также высотой треугольника ABC.
Теорема доказана.
Докажете данную теорему самостоятельно
Слайд 13 Мы установили, что биссектриса, медиана и высота равнобедренного треугольника,
1. Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
2. Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
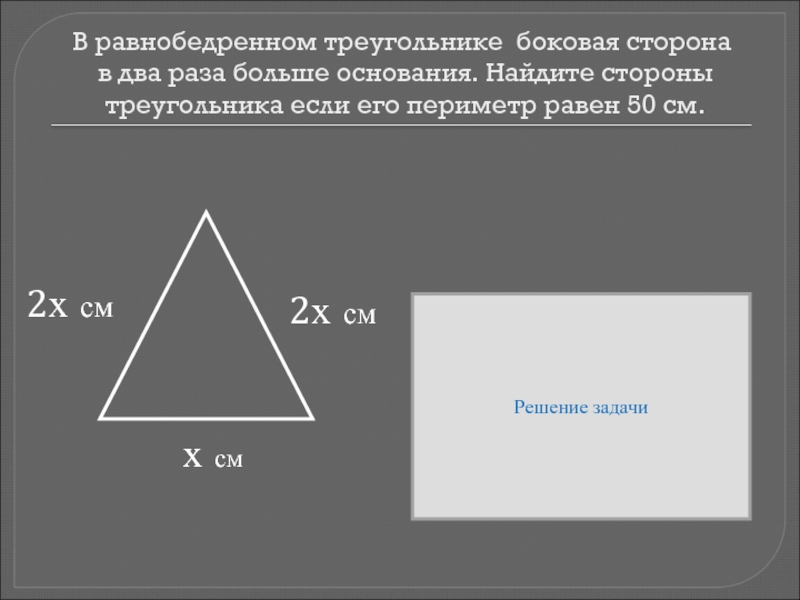
Слайд 15В равнобедренном треугольнике боковая сторона в два раза больше основания. Найдите
х см
2х см
2х см
Составим уравнение
х+2х+2х=50
5х=50
Х=10 (см)
Ответ: стороны треугольника равны 10 см, 20 см, 20 см.
Решение задачи
Слайд 16В равнобедренном треугольнике боковая сторона в два раза больше основания. Найдите
х см
2х см
2х см
Составим уравнение
х+2х+2х=50
5х=50
Х=10 (см)
Ответ: стороны треугольника равны 10 см, 20 см, 20 см.
Решение задачи
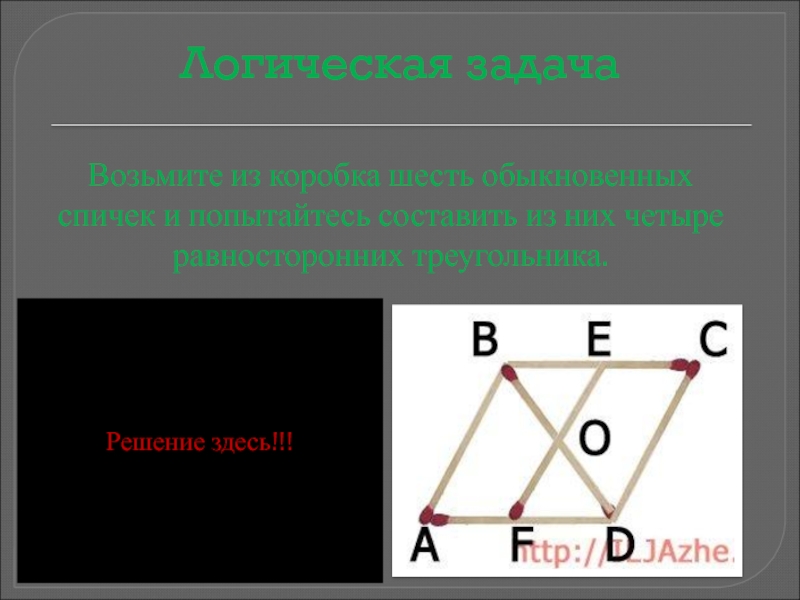
Слайд 19Логическая задача
Возьмите из коробка шесть обыкновенных спичек и попытайтесь составить из
Решение здесь!!!
Слайд 20Логическая задача
Возьмите из коробка шесть обыкновенных спичек и попытайтесь составить из
Решение здесь!!!