- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад студента по геометрии по теме Призма
Содержание
- 1. Презентация студента по геометрии по теме Призма
- 2. Призмой называется многогранник, две грани которого -угольники, а остальные граней — параллелограммы.Что такое призма?
- 3. История создания призмы Еще в древности
- 4. Одним из первых, который соединил обе эти
- 5. Подобно тому, как треугольник в понимании Евклида
- 6. Для того чтобы это определение было вполне
- 7. В памятниках вавилонской и древнеегипетской архитектуры встречаются
- 8. Часть геометрии, в которой изучаются свойства куба,
- 9. Евклид дает следующее определение призмы: “Призма есть
- 10. Термин “призма” греческого происхождения и буквально означает
- 11. О призме
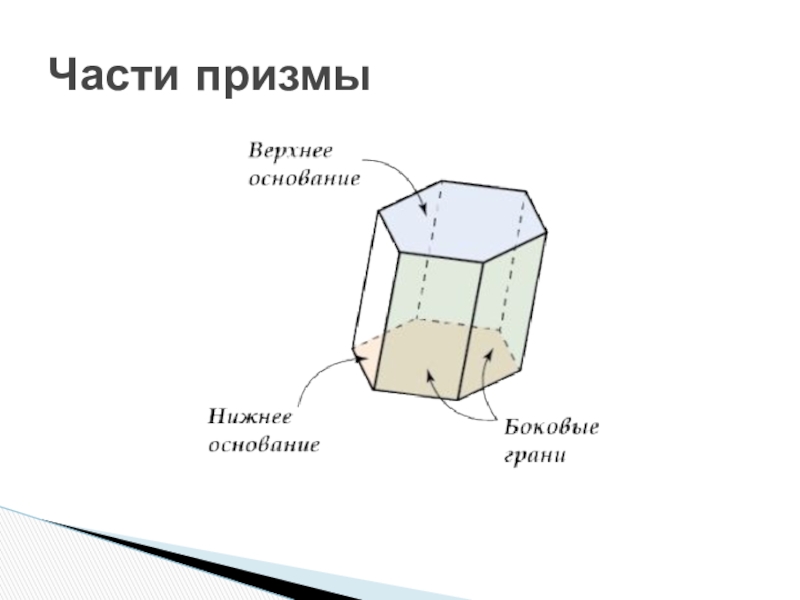
- 12. Части призмы
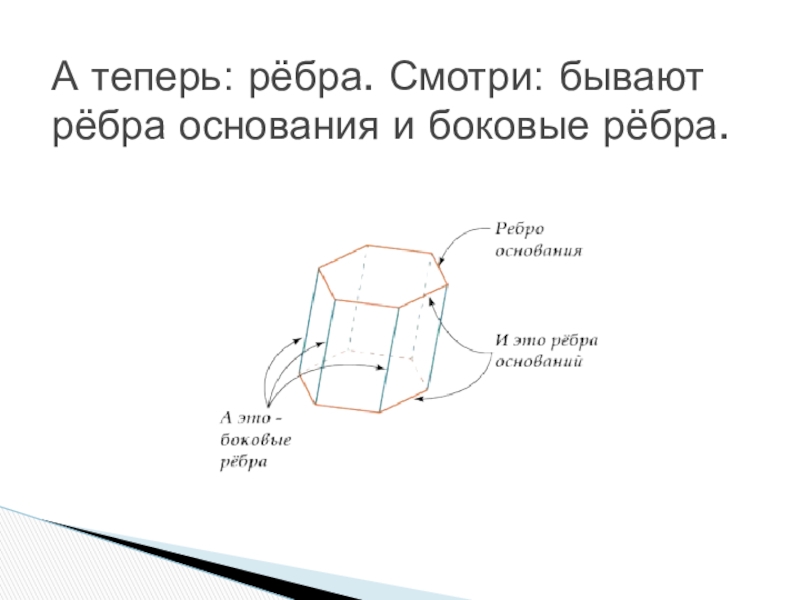
- 13. А теперь: рёбра. Смотри: бывают рёбра основания и боковые рёбра.
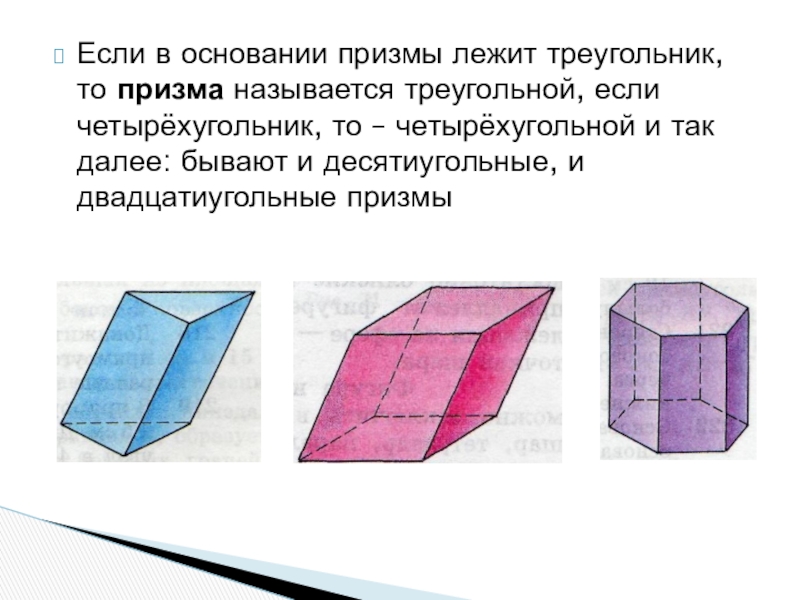
- 14. Если в основании призмы лежит треугольник, то призма называется
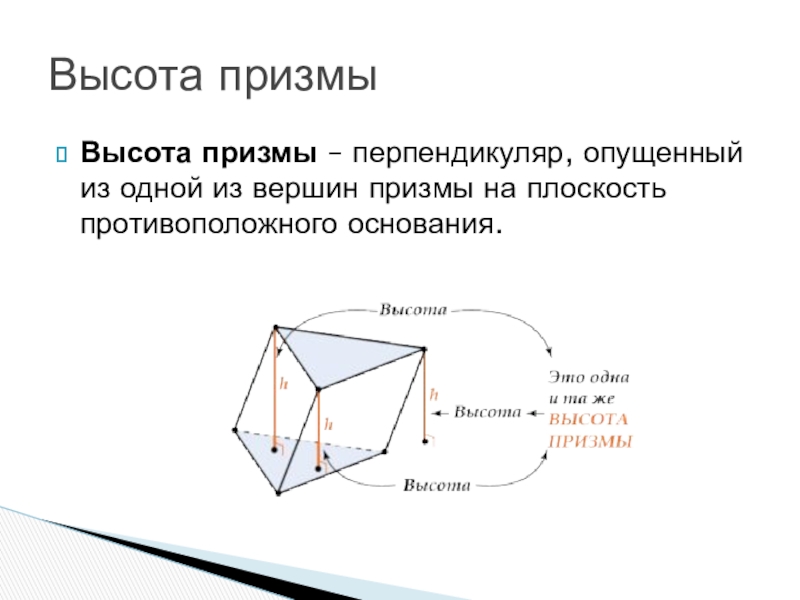
- 15. Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.Высота призмы
- 16. Если боковые рёбра призмы перпендикулярны основанию, то
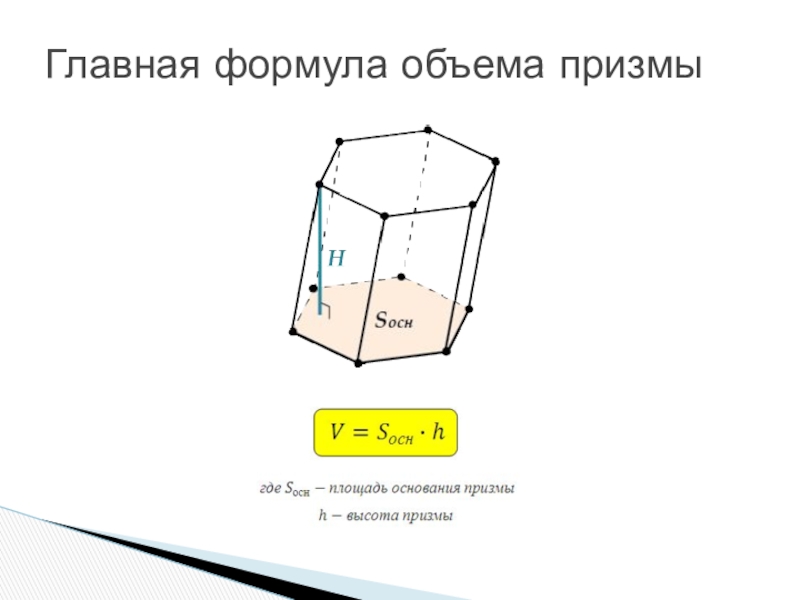
- 17. Главная формула объема призмы
- 18. Площадь поверхности призмы
- 19. Подготовил ПоповРафаэльСпасибо за внимание
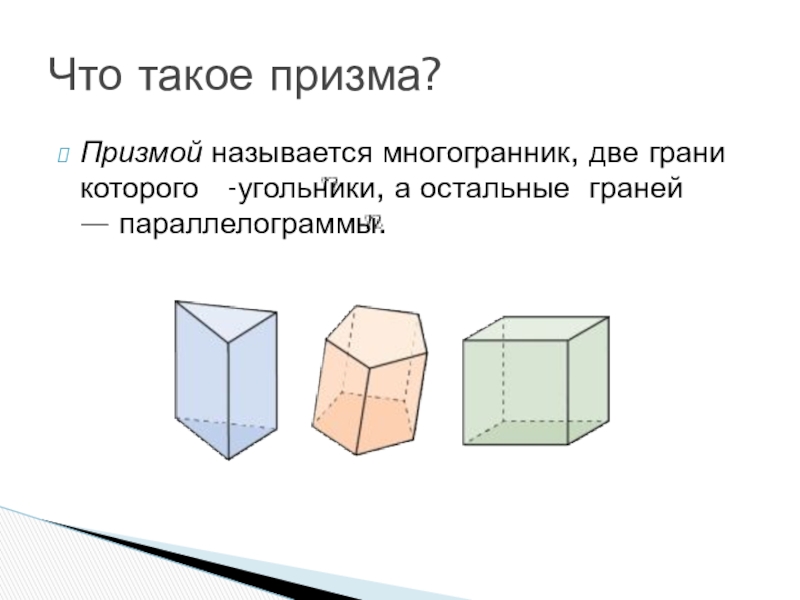
Призмой называется многогранник, две грани которого -угольники, а остальные граней — параллелограммы.Что такое призма?
Слайд 2Призмой называется многогранник, две грани которого -угольники, а остальные граней — параллелограммы.
Что такое
призма?
Слайд 3История создания призмы Еще в древности существовали два пути определения геометрических
понятий. Первый вел от фигур высшего порядка к фигурам низшего. Такой точки зрения придерживался, в частности, Евклид, определяющий поверхность как границу тела, линию - как границу поверхности, концы же линии - как точки. Второй путь ведет, наоборот, от фигур низшего измерения к фигурам высшего: движением точки образуется линия, аналогично из линий составляется поверхность и т. д.
История создания призмы
Слайд 4Одним из первых, который соединил обе эти точки зрения, был Герон
Александрийский, писавший, что тело ограничивается поверхностью и вместе с этим может быть рассмотрено как образованное движением поверхности. В появившихся позже на протяжении веков учебниках геометрии принималась за основу то одна, то другая, а иногда и обе вместе точки зрения.
Слайд 5Подобно тому, как треугольник в понимании Евклида не являются пустым, т.
е. представляет собой часть плоскости, ограниченную тремя неконкурентными (т. е. не пересекающимися в одной точке) отрезками, так и многогранник у него не пустой, не полый, а чем-то заполненный (по-нашему - частью пространства) . В античной математике, однако, понятия отвлеченного пространства еще не было. Евклид определяет призму как телесную фигуру, заключенную между двумя равными и параллельными плоскостями (основаниями) и с боковыми гранями - параллелограммами.
Слайд 6Для того чтобы это определение было вполне корректным, следовало бы, однако,
доказать, что плоскости, проходящие через пары непараллельных сторон оснований, пересекаются по параллельным прямым. Евклид употребляет термин “плоскость” как в широком смысле (рассматривая ее неограниченно продолженной во все направления) , так и в смысле конечной, ограниченной ее части, в частности грани, аналогично применению им термина “прямая” (в широком смысле - бесконечная прямая и в узком - отрезок) . В XVIII в. Тейлор дал такое определение призмы: это многогранник, у которого все грани, кроме двух, параллельны одной прямой.
Слайд 7В памятниках вавилонской и древнеегипетской архитектуры встречаются такие геометрические фигуры, как
куб, параллелепипед, призма. Важнейшей задачей египетской и вавилонской геометрии было определение объема различных пространственных фигур. Эта задача отвечала необходимости строить дома, дворцы, храмы и другие сооружения.
Слайд 8Часть геометрии, в которой изучаются свойства куба, призмы, параллелепипеда и других
геометрических тел и пространственных фигур, издавна называется стереометрией; Слово это греческого происхождения (“стереос” - пространственный, “метрео” - измеряю) и встречается еще у знаменитого древнегреческого философа Аристотеля. Стереометрия возникла позже, чем планиметрия.
Слайд 9Евклид дает следующее определение призмы: “Призма есть телесная (т. е. пространственная)
фигура, заключенная между плоскостями, из которых две противоположные равны и параллельны, остальные же - параллелограммы”. Тут, как и во многих других местах, Евклид употребляет термин “плоскость” не в смысле безгранично продолженной плоскости, а в смысле ограниченной ее части, грани, подобно тому как “прямая” означает у него и отрезок прямой.
Слайд 10Термин “призма” греческого происхождения и буквально означает “отпиленное” (тело) . Термин
“параллелепипедальное тело” встречается впервые у Евклида и означает дословно “параллеле-плоскостное тело”. Греческое слово “кубос” употребляется Евклидом в том же смысле, что и наше слово “куб”
Слайд 14Если в основании призмы лежит треугольник, то призма называется треугольной, если четырёхугольник, то
– четырёхугольной и так далее: бывают и десятиугольные, и двадцатиугольные призмы
Слайд 15Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость
противоположного основания.
Высота призмы
Слайд 16Если боковые рёбра призмы перпендикулярны основанию, то призма называется прямой.
У прямой
призмы:
все боковые грани прямоугольники;
все сечения проходящие через боковые рёбра – прямоугольники;
и даже сечения, проходящие только через одно боковое ребро - прямоугольники.
все боковые грани прямоугольники;
все сечения проходящие через боковые рёбра – прямоугольники;
и даже сечения, проходящие только через одно боковое ребро - прямоугольники.
Прямая призма