решений.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Решение геометрических задач по планиметрии профильного ЕГЭ
Содержание
- 1. Презентация Решение геометрических задач по планиметрии профильного ЕГЭ
- 2. Что собой представляют задания части №3?Задание №3 является геометрической
- 3. Для успешного решения задач типа №3 необходимо:Уметь
- 4. Для успешного решения задач типа №3 необходимо:Повторить
- 5. Рассмотрим решение задач №3:Задание 1Задание 2Задание 3Задание 4Задание 5Задание 6 Задание 7Задание 8 Задание 9
- 6. Задание:Найдите площадь части круга S, изображенного на
- 7. Решение: Площадь круга находиться по формуле: S= πR²,где
- 8. Задание:Найдите площадь части круга S, изображенного на
- 9. Решение:Площадь круга находиться по формуле: S= πR²,где R
- 10. Задание:Найдите площадь трапеции, изображенного на клетчатой бумаге
- 11. Решение:Площадь трапеции находиться по формуле: S=0,5*(a+b)*h,где а, b -
- 12. Задание:Найдите площадь трапеции, изображенного на клетчатой бумаге
- 13. Решение:Площадь трапеции находиться по формуле: S=0,5*(a+b)*h,где а, b -
- 14. Задание:Найдите площадь треугольника, изображенного на клетчатой бумаге
- 15. Решение:Площадь треугольника находиться по формуле: S=0,5*a*h,где а
- 16. Задание:Найдите площадь треугольника, изображенного на клетчатой бумаге
- 17. Решение:Площадь треугольника находиться по формуле: S=0,5*a*h,где а
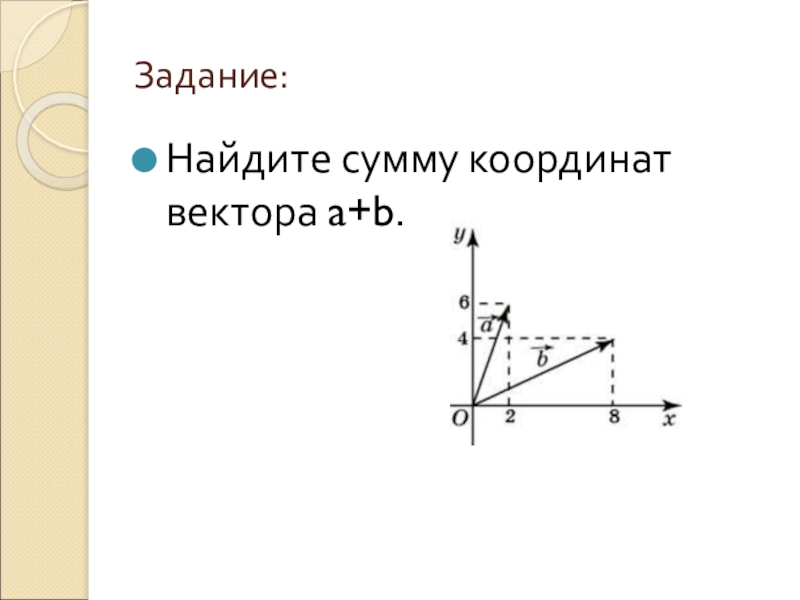
- 18. Задание:Найдите сумму координат вектора a+b.
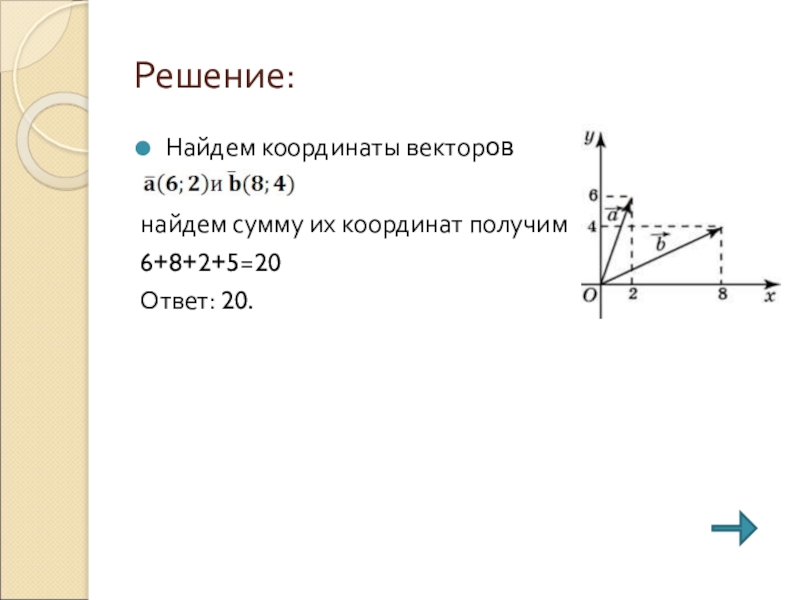
- 19. Решение:Найдем координаты векторовнайдем сумму их координат получим6+8+2+5=20 Ответ: 20.
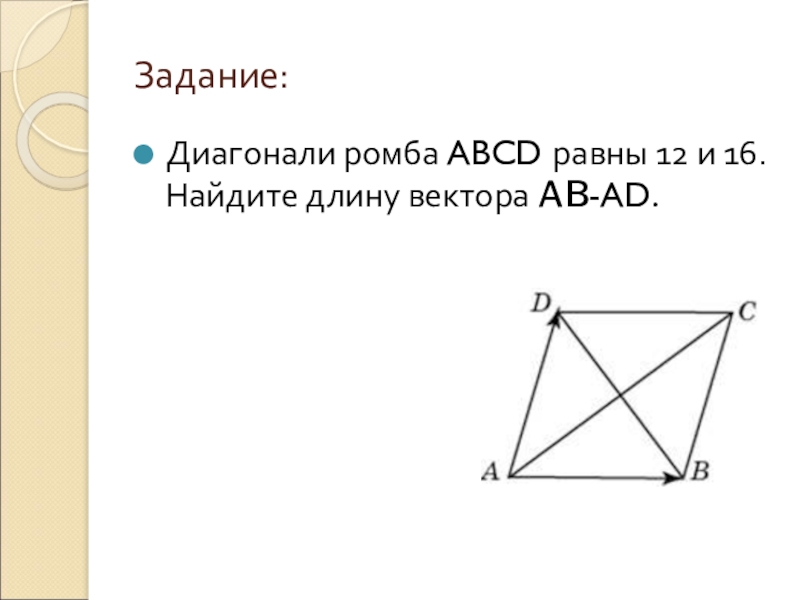
- 20. Задание:Диагонали ромба ABCD равны 12 и 16. Найдите длину вектора AB-AD.
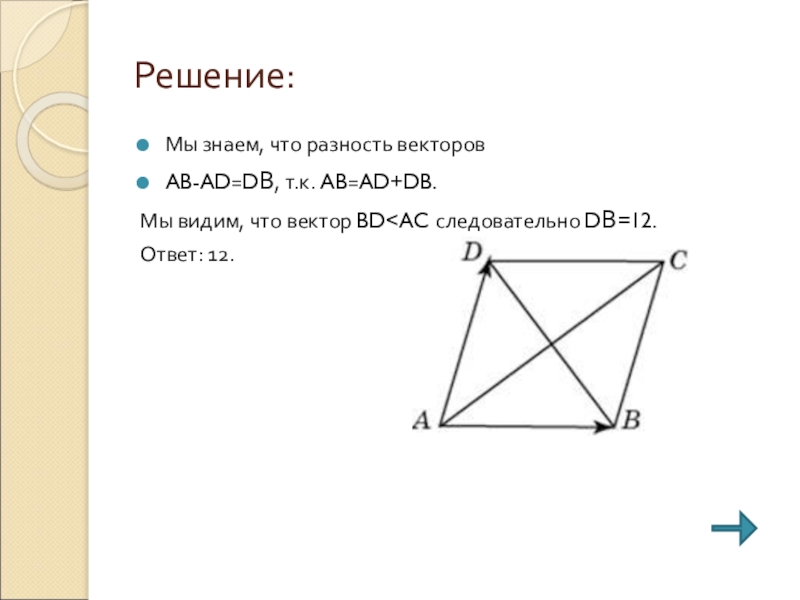
- 21. Решение:Мы знаем, что разность векторов AB-AD=DВ, т.к. AB=AD+DB.Мы видим, что вектор BD
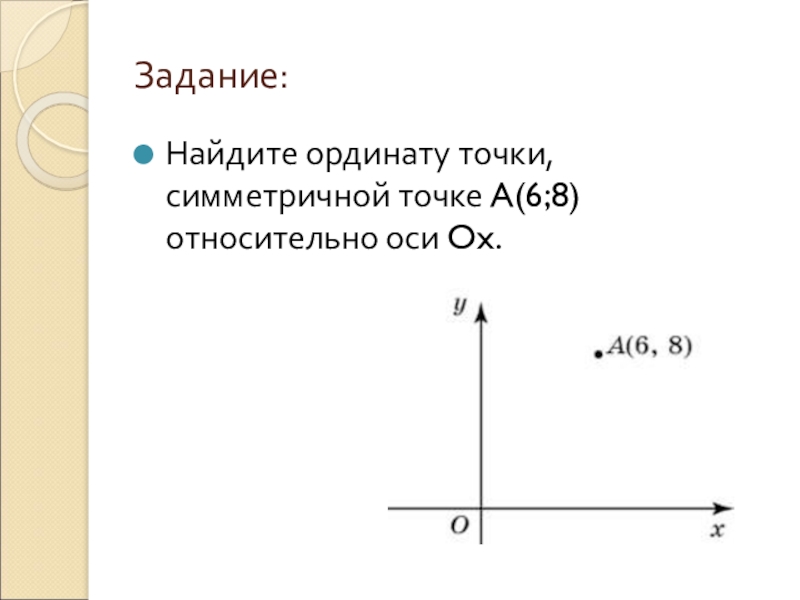
- 22. Задание:Найдите ординату точки, симметричной точке A(6;8) относительно оси Ox.
- 23. Решение:Точка симметричная относительна оси Ox будет точка
Что собой представляют задания части №3?Задание №3 является геометрической задачей.Задача настолько может быть легкой, что с ней может справиться и второклассник, впервые познакомившийся с понятием “площадь”.
Слайд 2Что собой представляют задания части №3?
Задание №3 является геометрической задачей.
Задача настолько может быть
легкой, что с ней может справиться и второклассник, впервые познакомившийся с понятием “площадь”.
Слайд 3Для успешного решения задач типа №3 необходимо:
Уметь выполнять действия с геометрическими
фигурами, координатами векторами.
Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей).
Моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин.
Решать планиметрические задачи на нахождение геометрических величин (длин, углов, площадей).
Моделировать реальные ситуации на языке геометрии, исследовать построенные модели с использованием геометрических понятий и теорем, аппарата алгебры; решать практические задачи, связанные с нахождением геометрических величин.
Слайд 4Для успешного решения задач типа №3 необходимо:
Повторить материал по темам:
Планиметрия.
Треугольник.
Параллелограмм, прямоугольник,
ромб, квадрат.
Трапеция.
Окружность и круг.
Площадь треугольника, параллелограмма, трапеции, круга, сектора.
Трапеция.
Окружность и круг.
Площадь треугольника, параллелограмма, трапеции, круга, сектора.
Слайд 5Рассмотрим решение задач №3:
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Задание
7
Задание 8
Задание 9
Задание 8
Задание 9
Слайд 6Задание:
Найдите площадь части круга S, изображенного на клетчатой бумаге с размером
клетки 1 см x 1 см. В ответ запишите S/ π .
Слайд 7Решение:
Площадь круга находиться по формуле:
S= πR²,
где R - радиус.
В нашем случае
R = 3 см.
Однако на рисунке заштрихован не весь круг, а лишь его четвертинка (т.к. угол между двумя радиусами, которые ограничивают заштрихованную часть составляет 90º)
Тогда площадь заштрихованной части S = 0,25π * 3² = 2,25 π (кв.см)
Ответ: 2,25
Однако на рисунке заштрихован не весь круг, а лишь его четвертинка (т.к. угол между двумя радиусами, которые ограничивают заштрихованную часть составляет 90º)
Тогда площадь заштрихованной части S = 0,25π * 3² = 2,25 π (кв.см)
Ответ: 2,25
Слайд 8Задание:
Найдите площадь части круга S, изображенного на клетчатой бумаге с размером
клетки 1 см x 1 см. В ответ запишите S/ π .
Слайд 9 Решение:
Площадь круга находиться
по формуле: S= πR²,
где R - радиус.
В нашем случае
R = 2 см.
Однако на рисунке заштрихован не весь круг, а лишь его четвертинка (т.к. угол между двумя радиусами, которые ограничивают заштрихованную часть составляет 90º)
Тогда площадь заштрихованной части S = 0,25* π * 2² = π (кв.см)
Ответ: 1
Однако на рисунке заштрихован не весь круг, а лишь его четвертинка (т.к. угол между двумя радиусами, которые ограничивают заштрихованную часть составляет 90º)
Тогда площадь заштрихованной части S = 0,25* π * 2² = π (кв.см)
Ответ: 1
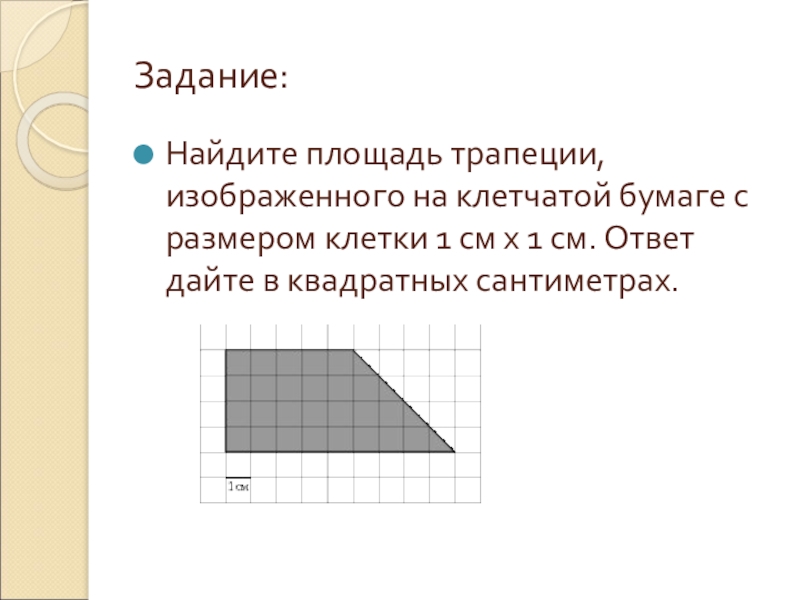
Слайд 10Задание:
Найдите площадь трапеции, изображенного на клетчатой бумаге с размером клетки 1
см x 1 см. Ответ дайте в квадратных сантиметрах.
Слайд 11Решение:
Площадь трапеции находиться
по формуле: S=0,5*(a+b)*h,
где а, b - основания трапеции; h -
ее высота.
В нашем случае а = 9 см; b = 5 см; h = 4 см.
Тогда S = 0,5*(9+5)*4 = 28 (кв.см)
Ответ: 28 кв.см
В нашем случае а = 9 см; b = 5 см; h = 4 см.
Тогда S = 0,5*(9+5)*4 = 28 (кв.см)
Ответ: 28 кв.см
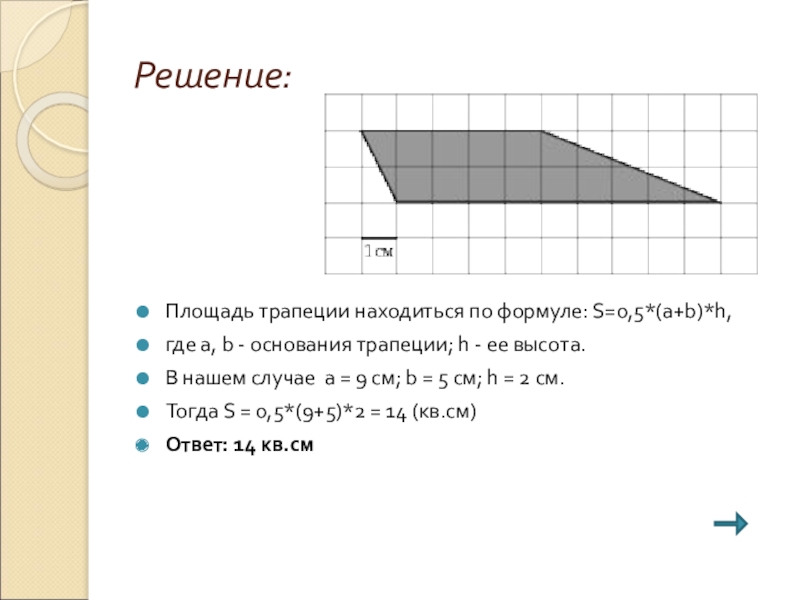
Слайд 12Задание:
Найдите площадь трапеции, изображенного на клетчатой бумаге с размером клетки 1
см x 1 см. Ответ дайте в квадратных сантиметрах.
Слайд 13Решение:
Площадь трапеции находиться по формуле: S=0,5*(a+b)*h,
где а, b - основания трапеции; h -
ее высота.
В нашем случае а = 9 см; b = 5 см; h = 2 см.
Тогда S = 0,5*(9+5)*2 = 14 (кв.см)
Ответ: 14 кв.см
В нашем случае а = 9 см; b = 5 см; h = 2 см.
Тогда S = 0,5*(9+5)*2 = 14 (кв.см)
Ответ: 14 кв.см
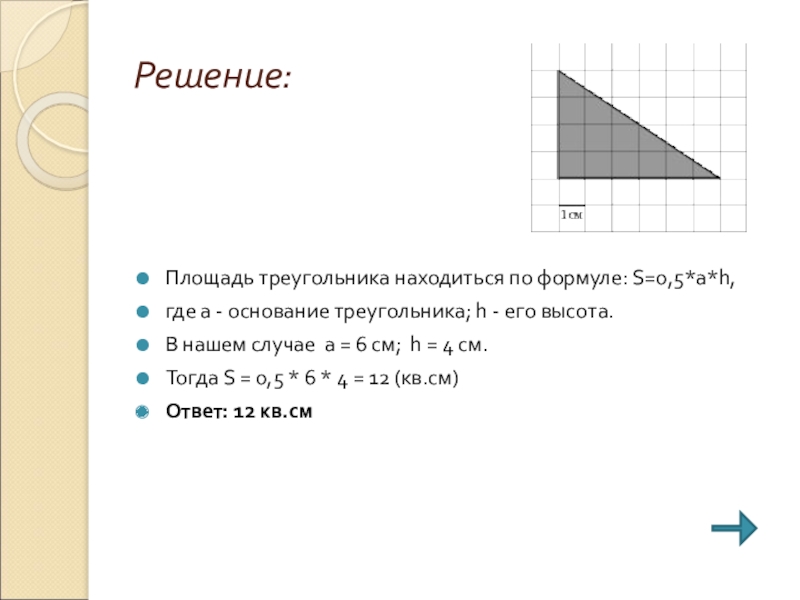
Слайд 14Задание:
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1
см x 1 см. Ответ дайте в квадратных сантиметрах.
Слайд 15Решение:
Площадь треугольника находиться по формуле: S=0,5*a*h,
где а - основание треугольника; h
- его высота.
В нашем случае а = 6 см; h = 4 см.
Тогда S = 0,5 * 6 * 4 = 12 (кв.см)
Ответ: 12 кв.см
В нашем случае а = 6 см; h = 4 см.
Тогда S = 0,5 * 6 * 4 = 12 (кв.см)
Ответ: 12 кв.см
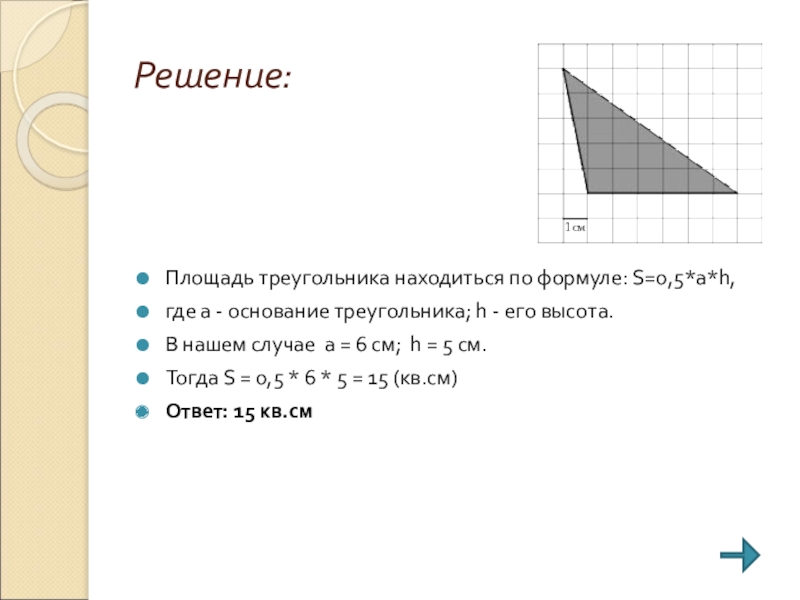
Слайд 16Задание:
Найдите площадь треугольника, изображенного на клетчатой бумаге с размером клетки 1
см x 1 см. Ответ дайте в квадратных сантиметрах.
Слайд 17Решение:
Площадь треугольника находиться по формуле: S=0,5*a*h,
где а - основание треугольника; h
- его высота.
В нашем случае а = 6 см; h = 5 см.
Тогда S = 0,5 * 6 * 5 = 15 (кв.см)
Ответ: 15 кв.см
В нашем случае а = 6 см; h = 5 см.
Тогда S = 0,5 * 6 * 5 = 15 (кв.см)
Ответ: 15 кв.см
Слайд 21Решение:
Мы знаем, что разность векторов
AB-AD=DВ, т.к. AB=AD+DB.
Мы видим, что вектор
BDОтвет: 12.
Слайд 23Решение:
Точка симметричная относительна оси Ox будет точка B(6;-8), т.к. нам нужно
найти ординату, а это y, то она будет равняться
y=-8.
Ответ: -8.
y=-8.
Ответ: -8.