- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Преобразование плоскости на себя
Содержание
- 1. Презентация Преобразование плоскости на себя
- 2. Отображение плоскости на себя.Любая точка плоскости оказывается сопоставленной некоторой точке.
- 3. Преобразование одной фигуры в другую называется движением,
- 4. СВОЙСТВА ДВИЖЕНИЯ1)При движении прямые переходят в прямые,
- 5. Понятие движения в геометрии связано с обычным
- 6. ВИДЫ ДВИЖЕНИЙОСЕВАЯ СИММЕТРИЯЦЕНТРАЛЬНАЯ СИММЕТРИЯПОВОРОТПАРАЛЛЕЛЬНЫЙ ПЕРЕНОС
- 7. Два движения, выполненные последовательно, снова дают движение.
- 8. ОВ1А1С1пример центр. симметрииЦентр. симметрия
- 9. В итоге: Чтобы построить фигуру, симметричную данной
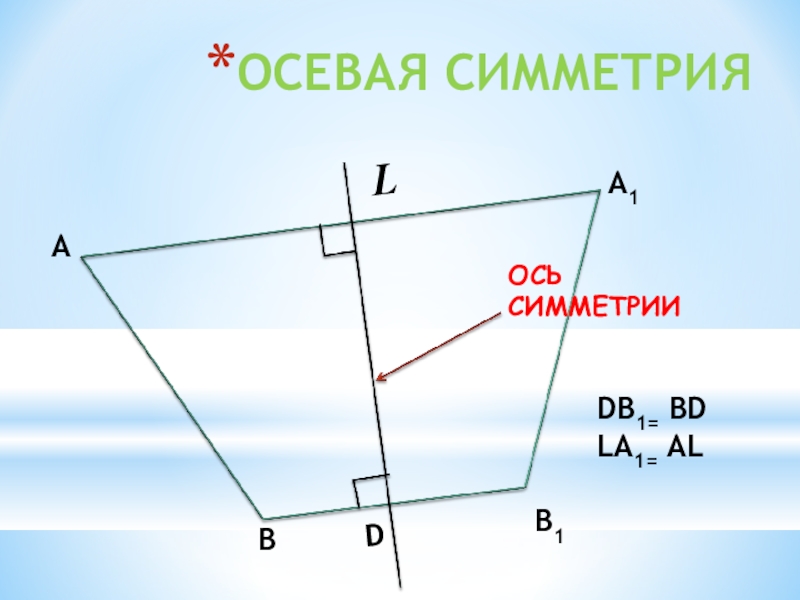
- 10. ОСЕВАЯ СИММЕТРИЯАВА1B1LDB1= BDLА1= ALD
- 11. Осевая симметрия- симметрия относительно прямой. чтобы
- 12. С симметрией мы часто встречаемся в быту,архитектуре,технике,природе.
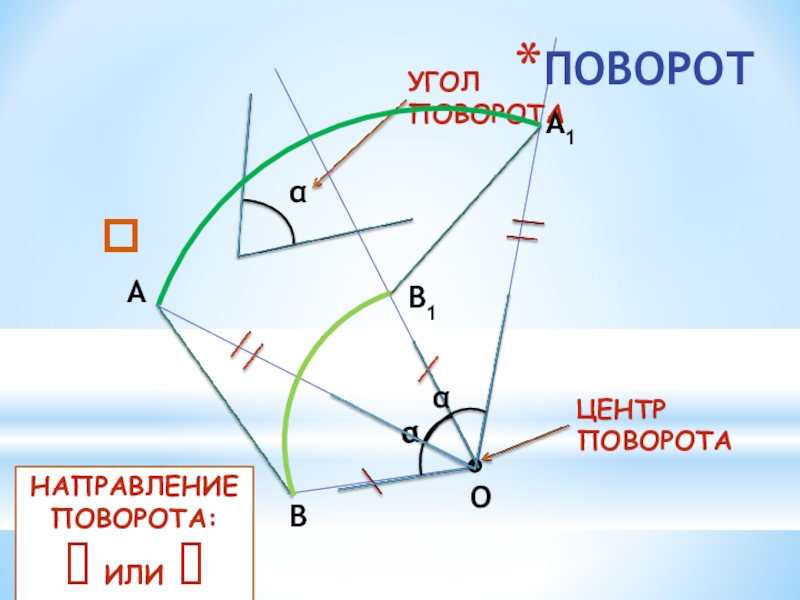
- 13. ПОВОРОТОАВА1В1НАПРАВЛЕНИЕ ПОВОРОТА:? ИЛИ ⮷?
- 14. ПОВОРОТ - движение, при котором по крайней
- 15. Параллельным переносом называется такое движение , при
Отображение плоскости на себя.Любая точка плоскости оказывается сопоставленной некоторой точке.
Слайд 2Отображение плоскости на себя.
Любая точка плоскости оказывается
сопоставленной некоторой точке.
Слайд 3Преобразование одной фигуры в другую называется движением, в том случае, если
оно сохраняет расстояние между точками.
B
AB = A1B1
B1
Слайд 4СВОЙСТВА ДВИЖЕНИЯ
1)При движении прямые переходят в прямые, полупрямые – в полупрямые,
отрезки – в отрезки.
2) Точки, лежащие на одной прямой, переходят в точки, лежащие на другой прямой, и порядок их взаимного расположения сохраняется.
3) Углы между полупрямыми также сохраняются.
2) Точки, лежащие на одной прямой, переходят в точки, лежащие на другой прямой, и порядок их взаимного расположения сохраняется.
3) Углы между полупрямыми также сохраняются.
Слайд 5
Понятие движения в геометрии связано с обычным представлением
о перемещении. Но, если
говоря о перемещении, мы представляем себе
непрерывный процесс, то в геометрии для нас будут иметь значение
только начальное и конечное положения фигур.
Слайд 9В итоге: Чтобы построить фигуру, симметричную данной относительно точки О, нужно: 1)) каждую
точку фигуры соединить с точкой О
2)продолжить полученный отрезок равным ему
3)отметить на конце этого отрезка образ исходной точки, затем соединить полученные образы.
Слайд 11Осевая симметрия- симметрия относительно прямой. чтобы построить фигуру, симметричную данной относительно
прямой LD, нужно:
1) из каждой точки фигуры провести перпендикуляр к прямой LD.
2) продолжить полученный отрезок равным ему,
3) отметить на конце этого отрезка образ исходной точки, затем соединить полученные образы.
FINISH
Слайд 14ПОВОРОТ - движение, при котором по крайней мере одна точка плоскости (пространства) остаётся
неподвижной.
Чтобы получить отображение фигуры при повороте около данной точки, нужно:
каждую точку фигуры повернуть на один и тот же угол в одном и том же направлении (по часовой стрелке или против часовой стрелки)
P.s. при движении угол переходит в равный ему угол.
Слайд 15Параллельным переносом называется такое движение , при котором все точки плоскости
перемещаются в одном и том же направлении на одинаковое расстояние.