- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме: Понятие правильного многогранника
Содержание
- 1. Презентация по теме: Понятие правильного многогранника
- 2. Многогранник – это поверхность,
- 3. В трёхмерном евклидовом пространстве существует всего пять правильных многогранников: Тетраэдр;Октаэдр;Икосаэдр;Гексаэдр или Куб;Додекаэдр.
- 4. Тетраэдр: Тетраэдр — простейший
- 5. Элементы симметрии тетраэдра.
- 6. Октаэдр: Октаэдр — многогранник с
- 7. Элементы симметрии октаэдра.
- 8. Икосаэдр: Икосаэдр — правильный
- 9. Элементы симметрии икосаэдра.
- 10. Гексаэдр или куб: Гексаэдр или
- 11. Элементы симметрии гексаэдра или куба. Ось
- 12. Додекаэдр: Додекаэдр состоит из
- 13. Элементы симметрии додекаэдра.
- 14. Многие формы многогранников придумал не сам человек,
Слайд 2 Многогранник – это поверхность, составленная из многоугольников и
Многогранники бывают выпуклые (Рис. 1) и невыпуклые (Рис. 2).
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
Выпуклый многогранник называется правильным, если все его грани – равные правильные многоугольники и, кроме того, в каждой его вершине сходится одно и то же число ребер.
Рис. 1
Рис. 2
Слайд 3В трёхмерном евклидовом пространстве существует всего пять правильных многогранников:
Тетраэдр;
Октаэдр;
Икосаэдр;
Гексаэдр или Куб;
Додекаэдр.
Слайд 4Тетраэдр:
Тетраэдр — простейший многогранник, гранями которого являются
У тетраэдра 4 грани, 4 вершины и 6 рёбер.
Тетраэдр, у которого все грани —равносторонние треугольники, называется правильным.
Сумма плоских углов при каждой вершине равна 180°.
Слайд 5Элементы симметрии тетраэдра.
Тетраэдр имеет три оси
Тетраэдр имеет 6 плоскостей симметрии, каждая из которых проходит через ребро тетраэдра перпендикулярно скрещивающемуся с ним ребру.
Плоскости симметрии тетраэдра.
Развертка тетраэдра.
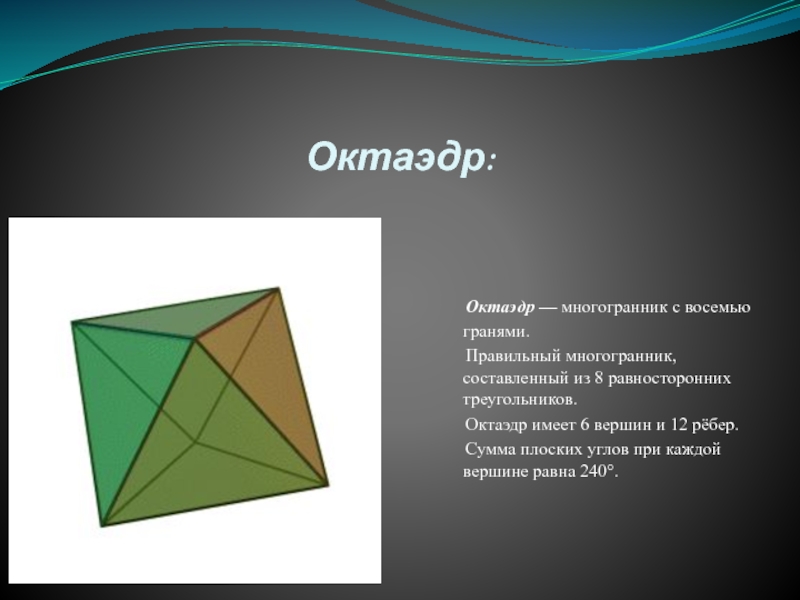
Слайд 6Октаэдр:
Октаэдр — многогранник с восемью гранями.
Октаэдр имеет 6 вершин и 12 рёбер.
Сумма плоских углов при каждой вершине равна 240°.
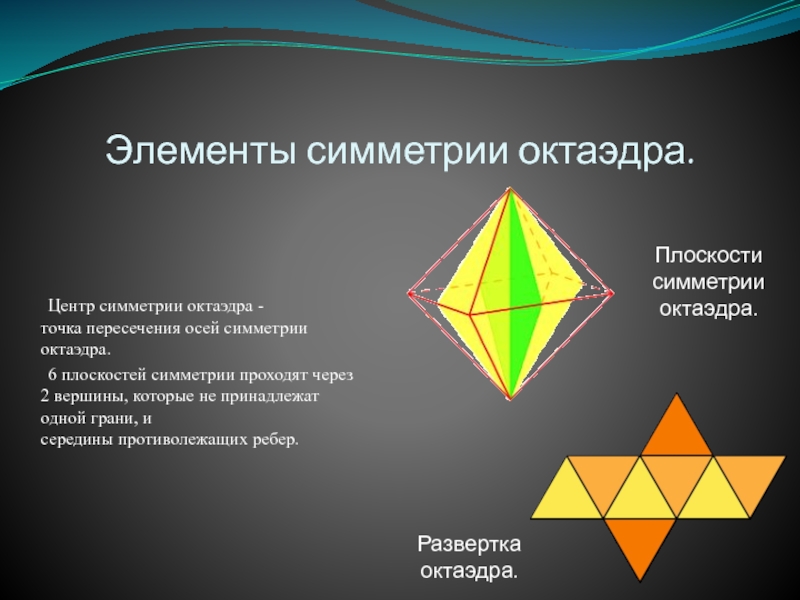
Слайд 7Элементы симметрии октаэдра.
Центр симметрии октаэдра -точка пересечения
6 плоскостей симметрии проходят через 2 вершины, которые не принадлежат одной грани, и середины противолежащих ребер.
Плоскости симметрии октаэдра.
Развертка октаэдра.
Слайд 8Икосаэдр:
Икосаэдр — правильный выпуклый многогранник, двадцатигранник.
Число ребер равно 30, число вершин — 12. Сумма плоских углов при каждой вершине равна 300°.
Слайд 9Элементы симметрии икосаэдра.
У икосаэдра, как
Точка пересечения этих осей икосаэдра – это и есть его центр симметрии.
Так же как и у додекаэдра, у икосаэдра 15 плоскостей симметрии.
Плоскости симметрии проходят через четыре вершины, которые лежат в одной плоскости, и середины противоположных параллельных ребер.
Плоскости симметрии икосаэдра.
Развертка икосаэдра.
Слайд 10Гексаэдр или куб:
Гексаэдр или куб — правильный многогранник,
У него 8 вершин, 12 ребер и 6 граней. Сумма плоских углов при вершине равна 270°.
Слайд 11Элементы симметрии гексаэдра или куба.
Ось симметрии куба может пролегать
Сквозь центр симметрии куба проходят 9 осей симметрии.
Плоскостей симметрии у куба тоже 9, они пролегают или через противолежащие ребра, или через середины противолежащих ребер.
Плоскости симметрии гексаэдра или куба.
Развертка гексаэдра или куба.
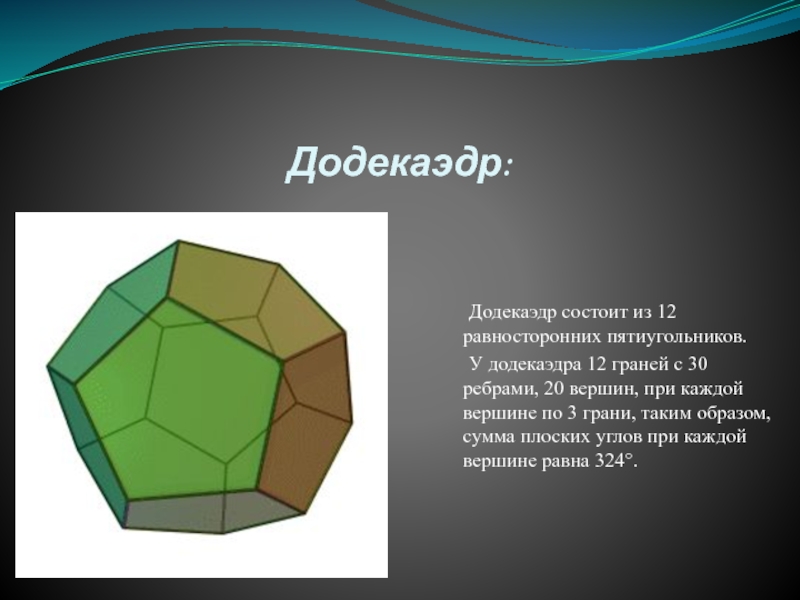
Слайд 12Додекаэдр:
Додекаэдр состоит из 12 равносторонних пятиугольников.
Слайд 13Элементы симметрии додекаэдра.
У додекаэдра центр симметрии состоит из
Все оси проходят через середины противоположных параллельных ребер.
Каждая из плоскостей симметрии проходит в каждой грани через вершину и середину противолежащего ребра.
Плоскости симметрии додекаэдра.
Развертка додекаэдра.
Слайд 14Многие формы многогранников придумал не сам человек, а их создала природа
Многогранники окружают нас повсюду: детские кубики, мебель, архитектурные сооружения и т. п. В повседневной жизни мы почти перестали их замечать, а ведь это очень интересно, знать историю привычных для всех предметов.