27
8Е класса
Филиппова Дарья
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Метод спрямления в решении геометрических задач
Содержание
- 1. Презентация по теме Метод спрямления в решении геометрических задач
- 2. Легенда о Дидоне
- 3. Открытия в области теории экстремальных величин.
- 4. Открытия в области теории экстремальных величин.«Решение задач
- 5. Методологический аппарат исследования Объект исследования: планиметрические задачи
- 6. Задача №1 Две деревни А и В
- 7. Задача №2Где следует построить мост через реку,
- 8. Задача Фаньяно ( треугольник Щварца)Найти треугольник наименьшего периметра, вписанного в данный остроугольный треугольник.
- 9. Список литературыАктершев С. П. Задачи на максимум
- 10. СПАСИБО ЗА ВНИМАНИЕ!
Легенда о Дидоне
Слайд 4Открытия в области теории экстремальных величин.
«Решение задач этого рода составляет предмет
так называемой теории наибольших и наименьших величин. Эти задачи, чисто практического характера, имеют особенную важность и для теории: все законы, определяющие движение материи весомой и невесомой, представляют решение задач этого рода. Нельзя не заметить особенно благотворного влияния их на развитие наук математических».
Слайд 5Методологический аппарат исследования
Объект исследования: планиметрические задачи на экстремум;
Предмет исследования: решение
экстремальных задач методом спрямления в геометрии;
Цель исследования заключается в рассмотрении решения задач методом спрямления, рассмотрение истории, понятий и методов решения задач на экстремум;
Задачи исследования:
изучить представленную научную литературу;
описать историю решения задач на экстремум;
рассмотреть метод спрямления в решении планиметрических задач на экстремум;
рассмотреть решение задачи Фаньяно.
Цель исследования заключается в рассмотрении решения задач методом спрямления, рассмотрение истории, понятий и методов решения задач на экстремум;
Задачи исследования:
изучить представленную научную литературу;
описать историю решения задач на экстремум;
рассмотреть метод спрямления в решении планиметрических задач на экстремум;
рассмотреть решение задачи Фаньяно.
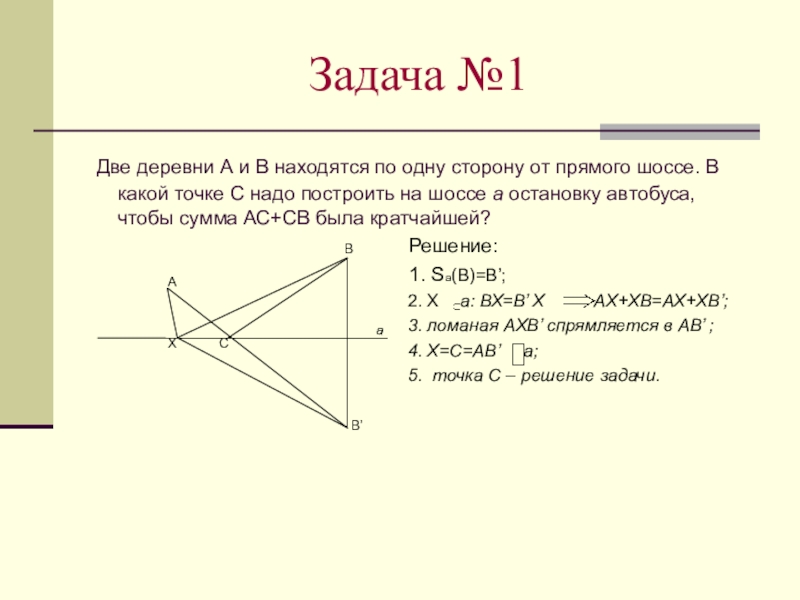
Слайд 6Задача №1
Две деревни А и В находятся по одну сторону
от прямого шоссе. В какой точке С надо построить на шоссе а остановку автобуса, чтобы сумма АС+СВ была кратчайшей?
Решение:
1. Sa(B)=B’;
2. X а: ВХ=В’ Х АХ+ХВ=АХ+ХВ’;
3. ломаная АХВ’ спрямляется в АВ’ ;
4. X=C=АВ’ a;
5. точка С – решение задачи.
Решение:
1. Sa(B)=B’;
2. X а: ВХ=В’ Х АХ+ХВ=АХ+ХВ’;
3. ломаная АХВ’ спрямляется в АВ’ ;
4. X=C=АВ’ a;
5. точка С – решение задачи.
Слайд 7Задача №2
Где следует построить мост через реку, разделяющую деревни А и
В, чтобы путь от А до В по этому мосту был кратчайшем? (берега реки параллельные прямые)
Решение:
1. min(L): L=AP+PQ+QB.
2. .
3. .
4. min(А’QB) ломанная A’QB
«спрямляется».
5. .
6. P’Q’ – решение задачи.
Решение:
1. min(L): L=AP+PQ+QB.
2. .
3. .
4. min(А’QB) ломанная A’QB
«спрямляется».
5. .
6. P’Q’ – решение задачи.
Слайд 8 Задача Фаньяно
( треугольник Щварца)
Найти треугольник наименьшего периметра, вписанного в
данный остроугольный треугольник.
Слайд 9Список литературы
Актершев С. П. Задачи на максимум и минимум. – «БХВ
Петербург» Санкт–Петербург, 2004.
Нагибин Ф. Ф. Экстремумы. – «Просвещение». – Москва, 1996.
Протасов В. Ю. Максимумы и минимумы в геометрии. – Издательство Московского центра непрерывного математического образования.- Москва, 2005.
Тихомиров В. М. Рассказы о максимумах и минимумах. Издание второе. – Издательство МЦНМО Москва, 2006.
Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Геометрические неравенства и задачи на максимум и минимум. – Издательство «Наука» Москва, 1970.
Нагибин Ф. Ф. Экстремумы. – «Просвещение». – Москва, 1996.
Протасов В. Ю. Максимумы и минимумы в геометрии. – Издательство Московского центра непрерывного математического образования.- Москва, 2005.
Тихомиров В. М. Рассказы о максимумах и минимумах. Издание второе. – Издательство МЦНМО Москва, 2006.
Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Геометрические неравенства и задачи на максимум и минимум. – Издательство «Наука» Москва, 1970.