- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по теме Лабиринты
Содержание
- 1. Презентация по теме Лабиринты
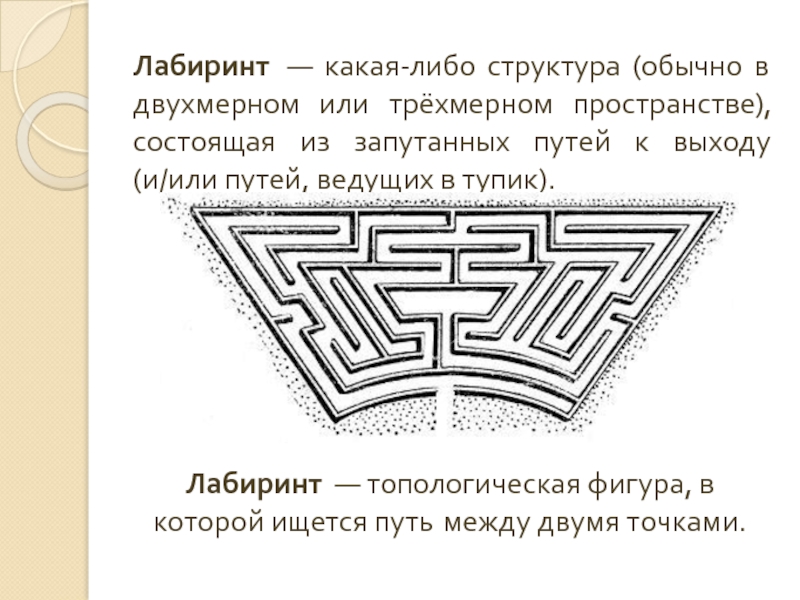
- 2. Лабиринт — какая-либо структура (обычно в двухмерном
- 3. Фаюмский лабиринт (расположен на севере Египта)В центре
- 4. Лабиринт был построен Дедалом на Крите по
- 5. План лабиринта «Беседка Розамунды»В Англии самым знаменитым
- 6. Мозаиками в форме лабиринтов украшены полы многих средневековых соборов Европы, например Шартрскогосвятого КвентинаСиенского
- 7. План лабиринта из живых изгородей в Хемптон-КортеВ
- 8. С математической точки зрения лабиринт представляет собой
- 9. Если есть карта лабиринта, то его можно
- 10. Алгоритм №1. Простой алгоритм прохождения лабиринтаНужно
- 11. Если же в лабиринте имеются замкнутые маршруты
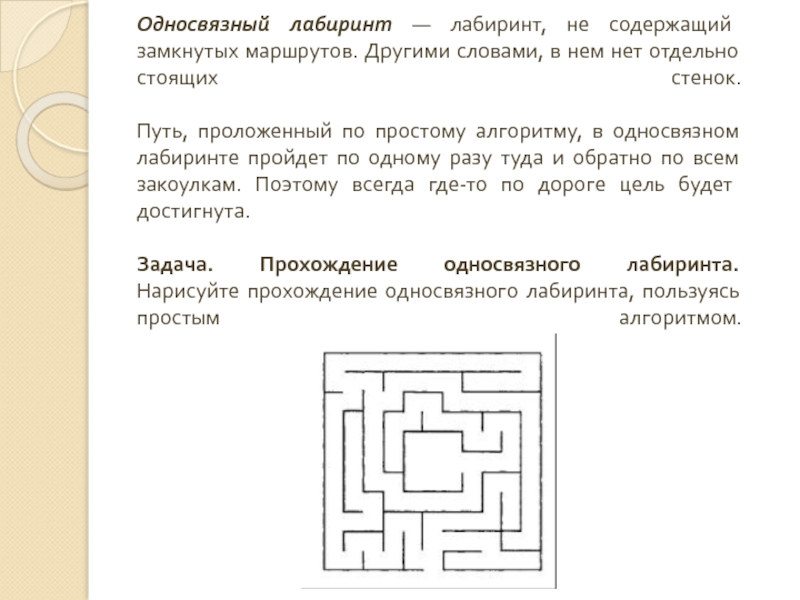
- 12. Односвязный лабиринт — лабиринт, не содержащий замкнутых
- 13. Многосвязный лабиринт имеет отдельно стоящие стенки.
- 14. Алгоритм №2 Прохождение многосвязного лабиринта1. Пробираясь по
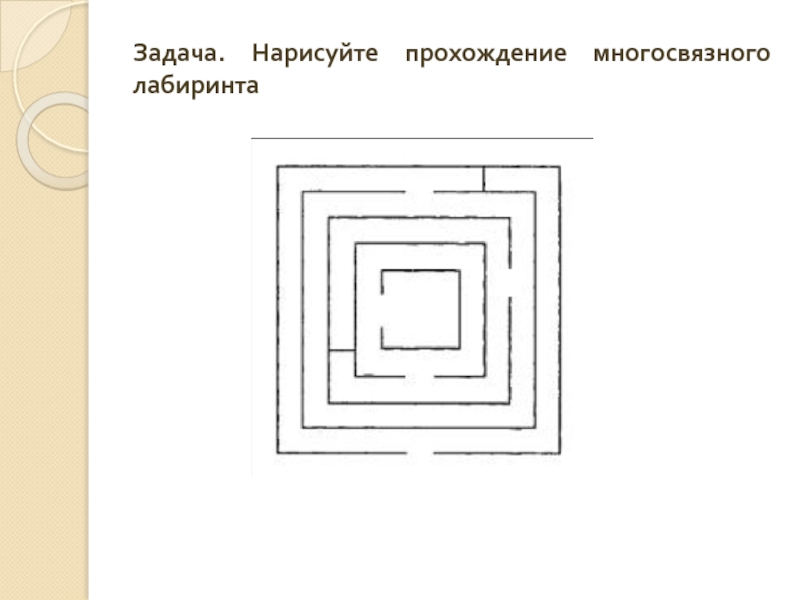
- 15. Задача. Нарисуйте прохождение многосвязного лабиринта
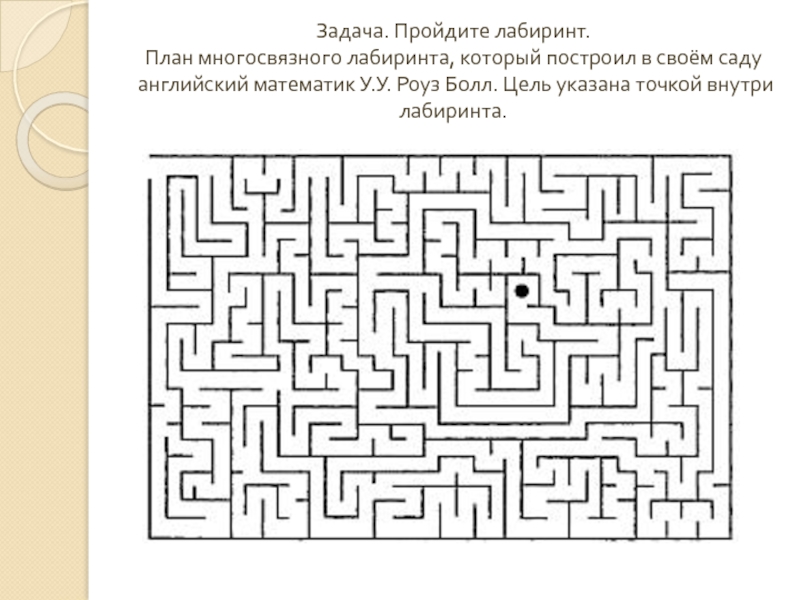
- 16. Задача. Пройдите лабиринт. План многосвязного лабиринта,
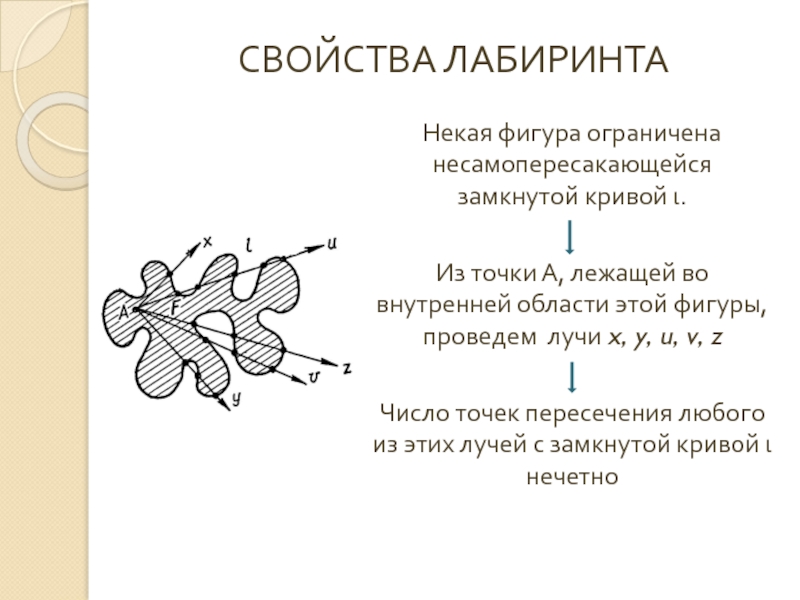
- 17. СВОЙСТВА ЛАБИРИНТАНекая фигура ограничена несамопересакающейся замкнутой кривой
- 18. Проведем дуги, которые начинаются в точке А,
- 19. ВНЕШНЯЯ ТОЧКА – если число точек пересечения
- 20. Из произвольной точки А проведем лучи, которые
- 21. РЕШЕНИЕ ЗАДАЧВ лабиринте даны точки А, В
- 22. РЕШЕНИЕ ЗАДАНИЯ № 1:Выясним в какой области
- 23. РЕШЕНИЕ ЗАДАНИЯ № 2:Определяем какие из этих
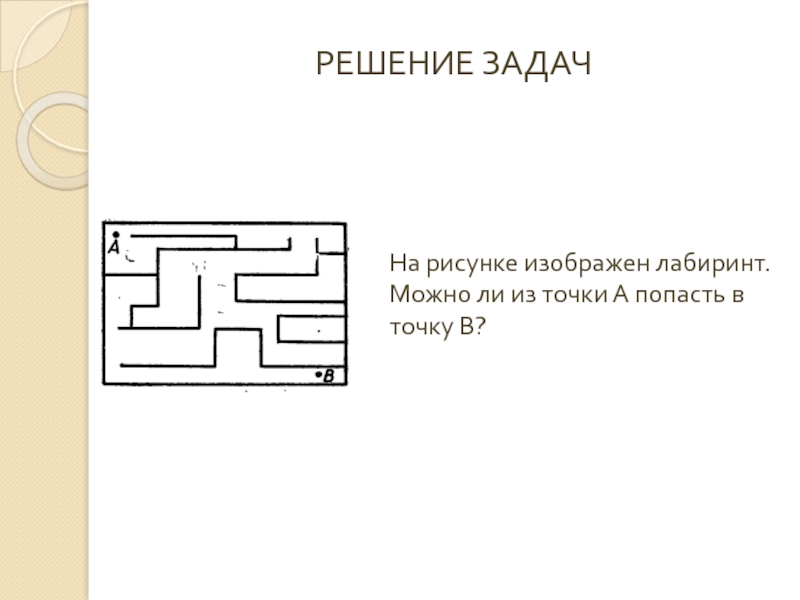
- 24. РЕШЕНИЕ ЗАДАЧНа рисунке изображен лабиринт. Можно ли из точки А попасть в точку В?
- 25. РЕШЕНИЕ:Необходимо выяснить, находятся ли точки А и
- 26. РЕШЕНИЕ ЗАДАЧНа рисунке изображен план здания. Требуется
- 27. РЕШЕНИЕ:Построим граф, соответствующий данной ситуации. Изобразим комнаты
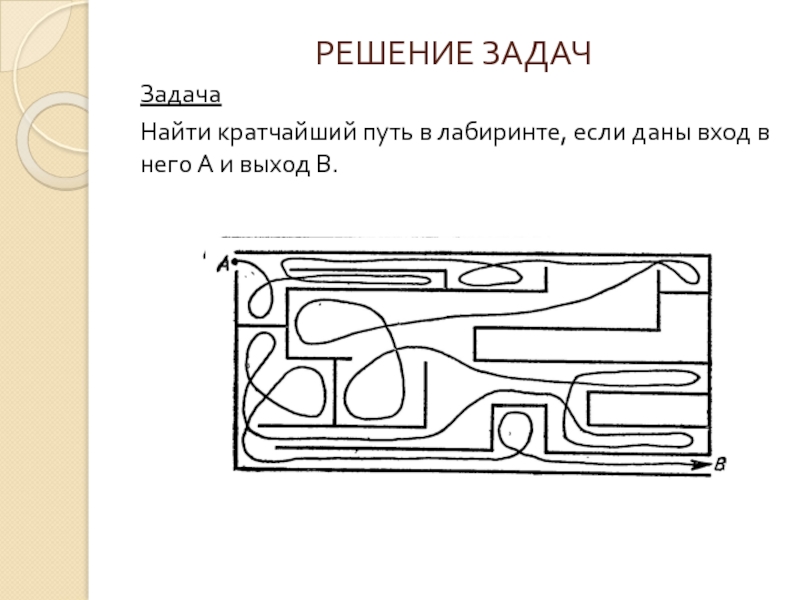
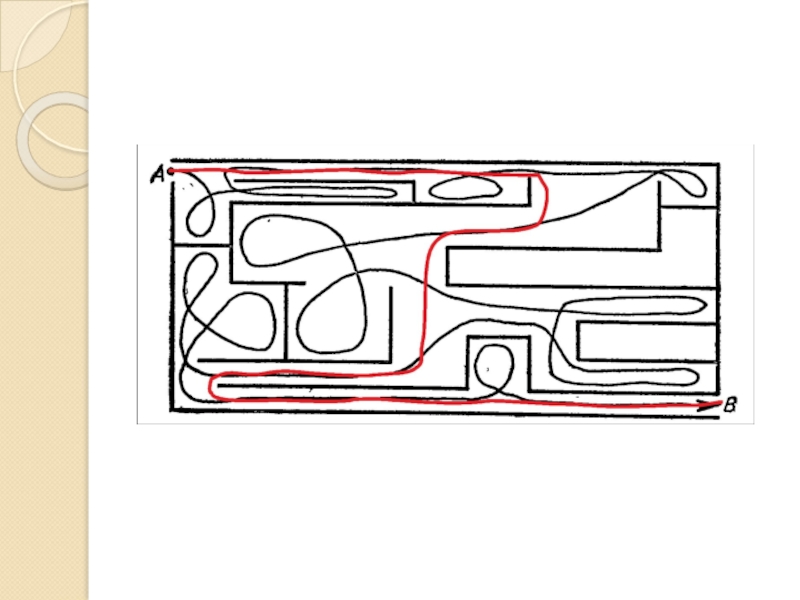
- 28. РЕШЕНИЕ ЗАДАЧЗадача Найти кратчайший путь в лабиринте, если даны вход в него А и выход В.
- 29. Решение: В лабиринте имеются запутывающие искусственные линии, т.к.
- 30. Слайд 30
- 31. ЗАДАЧИПомоги муравью добраться домой
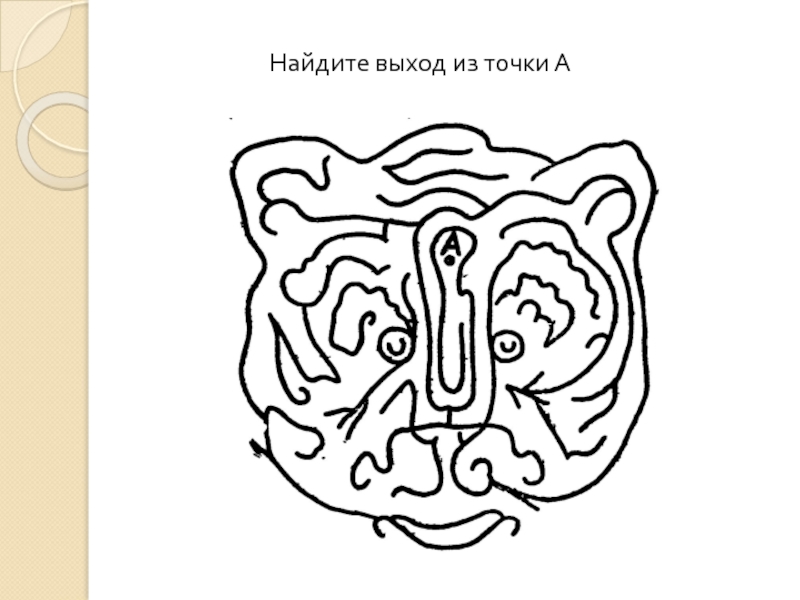
- 32. Найдите выход из точки А
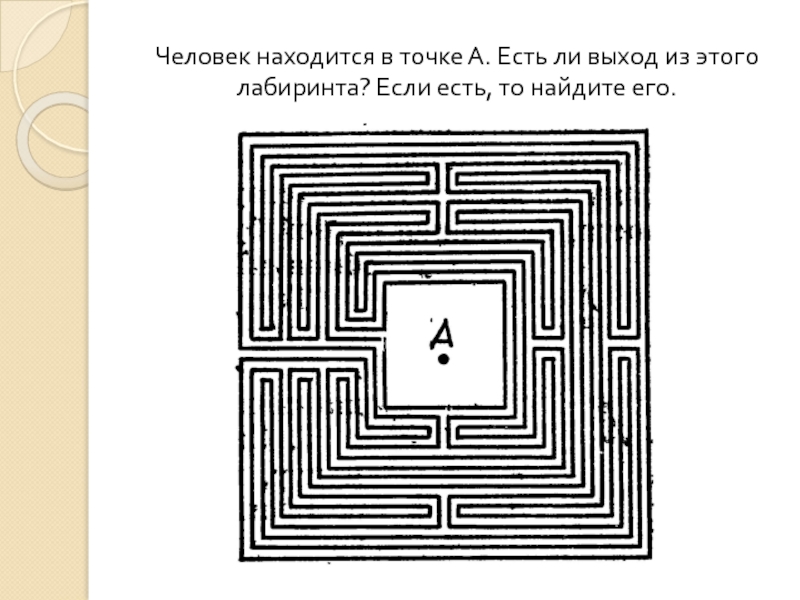
- 33. Человек находится в точке А. Есть ли выход из этого лабиринта? Если есть, то найдите его.
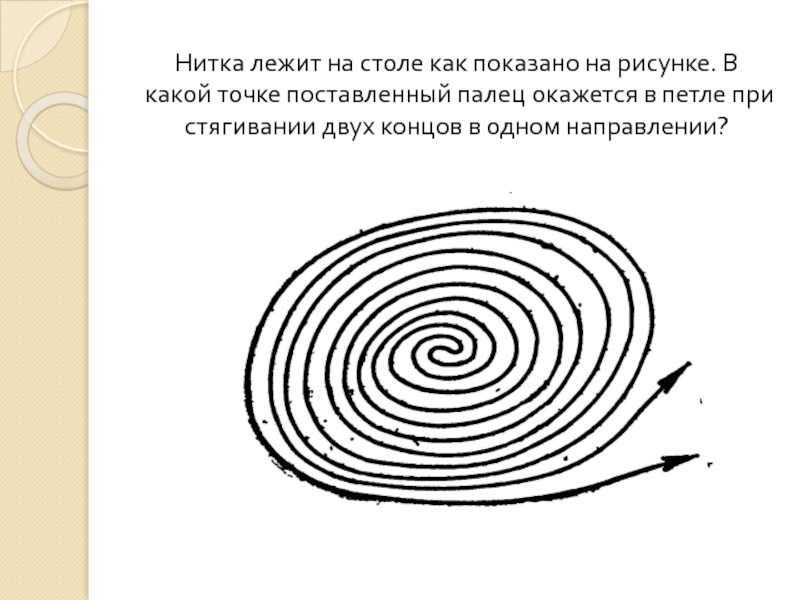
- 34. Нитка лежит на столе как показано на
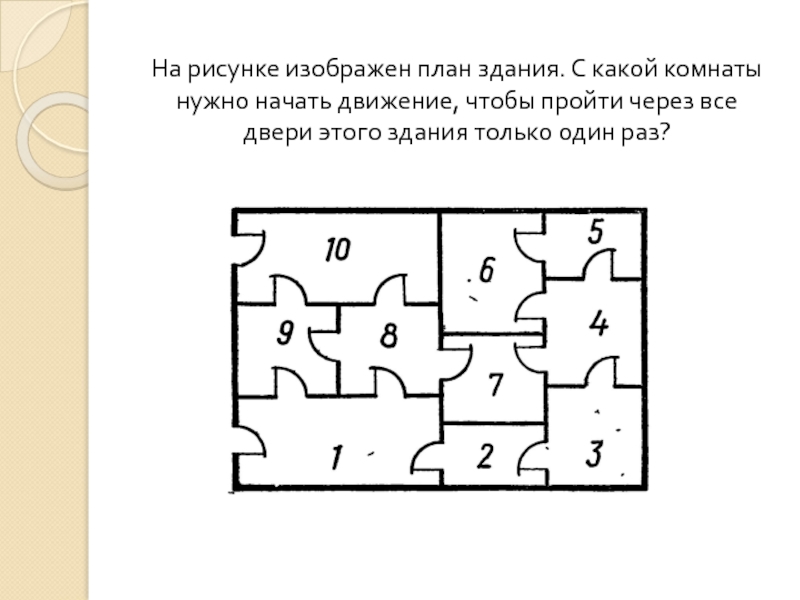
- 35. На рисунке изображен план здания. С какой
- 36. Даны точки A, B, C, D, E,
Слайд 2Лабиринт — какая-либо структура (обычно в двухмерном или трёхмерном пространстве), состоящая
Лабиринт — топологическая фигура, в которой ищется путь между двумя точками.
Слайд 3Фаюмский лабиринт
(расположен на севере Египта)
В центре Фаюмской области один из правителей
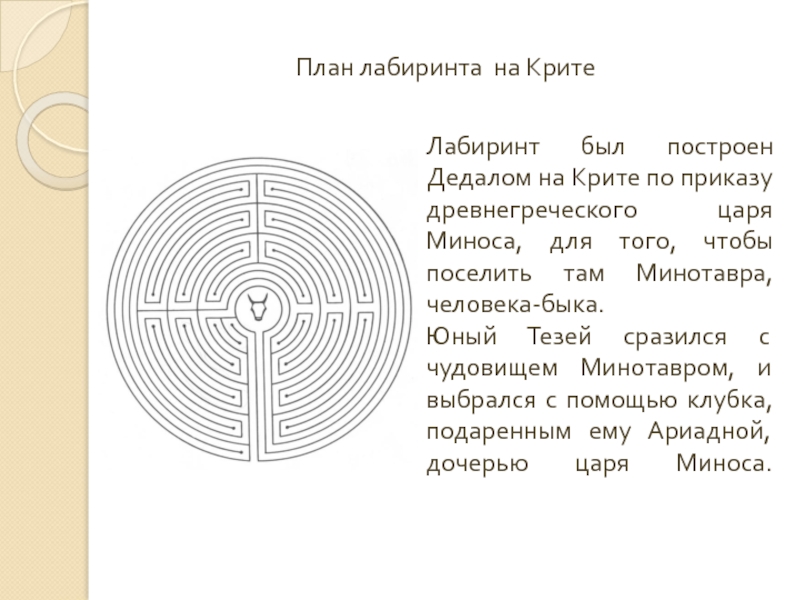
Слайд 4Лабиринт был построен Дедалом на Крите по приказу древнегреческого царя Миноса,
План лабиринта на Крите
Слайд 5План лабиринта «Беседка Розамунды»
В Англии самым знаменитым архитектурным лабиринтом была беседка
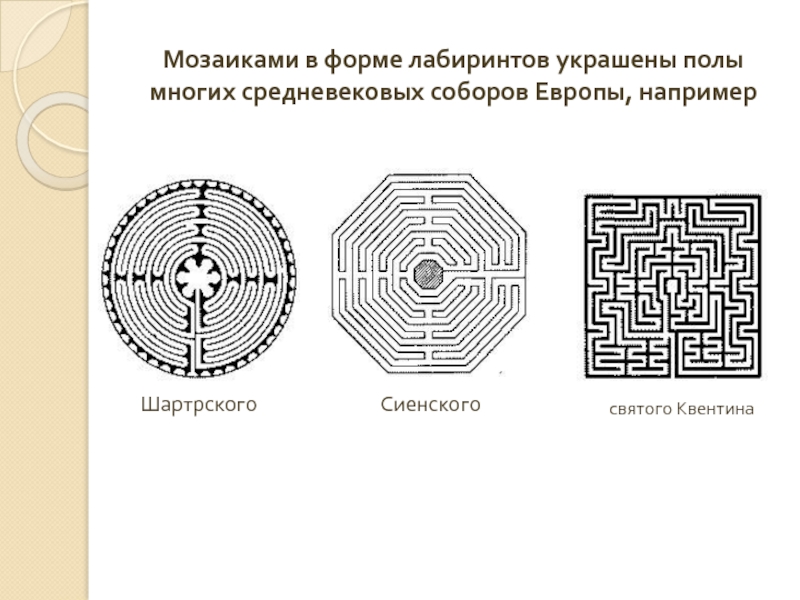
Слайд 6Мозаиками в форме лабиринтов украшены полы многих средневековых соборов Европы, например
Шартрского
святого Квентина
Сиенского
Слайд 7План лабиринта из живых изгородей в Хемптон-Корте
В Англии самый известный лабиринт
Слайд 8С математической точки зрения лабиринт представляет собой топологическую задачу. Если его
Слайд 9Если есть карта лабиринта, то его можно решить очень быстро: достаточно
Если у лабиринта только один вход, а задача состоит в нахождении дороги к единственному выходу, то такая задача всегда решается по следующему алгоритму. Правда, такой путь вряд ли будет кратчайщим.
Слайд 10Алгоритм №1.
Простой алгоритм прохождения лабиринта
Нужно идти по лабиринту, все время
Задача. Простое прохождение лабиринта.
Нарисуйте прохождение лабиринта в Хэмптон-Корте, пользуясь простым алгоритмом.
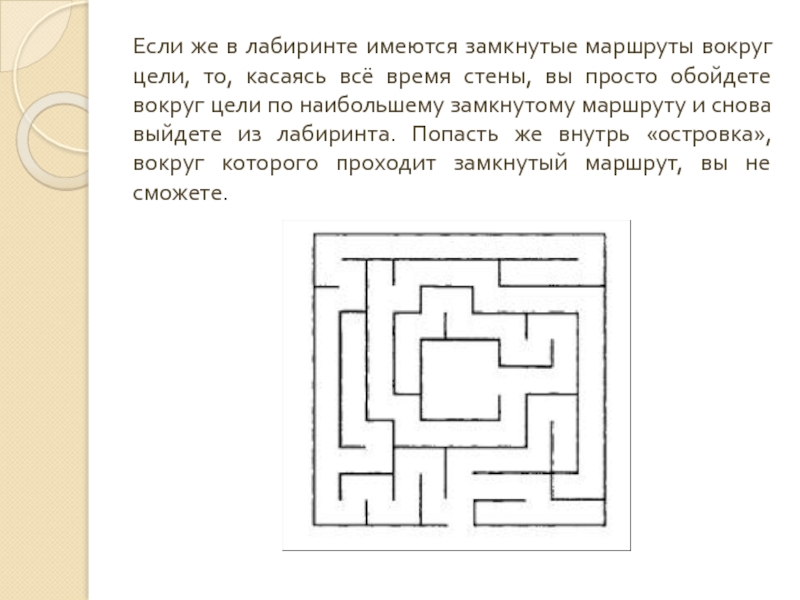
Слайд 11Если же в лабиринте имеются замкнутые маршруты вокруг цели, то, касаясь
Слайд 12Односвязный лабиринт — лабиринт, не содержащий замкнутых маршрутов. Другими словами, в
Слайд 13Многосвязный лабиринт имеет отдельно стоящие стенки. Целью лабиринта в Хэмптон-Корте служит центральная
Слайд 14Алгоритм №2
Прохождение многосвязного лабиринта
1. Пробираясь по лабиринту, все время отмечаем путь,
2. Дойдя до разветвления, выбираем любой новый путь.
3. Если, идя по новому пути (где нет линии вдоль левой стенки):
а) попадаем в тупик;
б) выходим на какой-нибудь перекресток, где уже были,— то поворачиваем обратно.
4. Если, идя по старому пути (где есть линия вдоль левой стенки),
выходим к перекрестку, то:
а) если есть новый путь, то выбираем его;
б) если нет нового пути, то идем по старому.
5. Никогда не пойдем по пути с отметками по обеим сторонам.
Слайд 16Задача. Пройдите лабиринт. План многосвязного лабиринта, который построил в своём саду
Слайд 17СВОЙСТВА ЛАБИРИНТА
Некая фигура ограничена несамопересакающейся замкнутой кривой ι.
Из точки А, лежащей
Число точек пересечения любого из этих лучей с замкнутой кривой ι нечетно
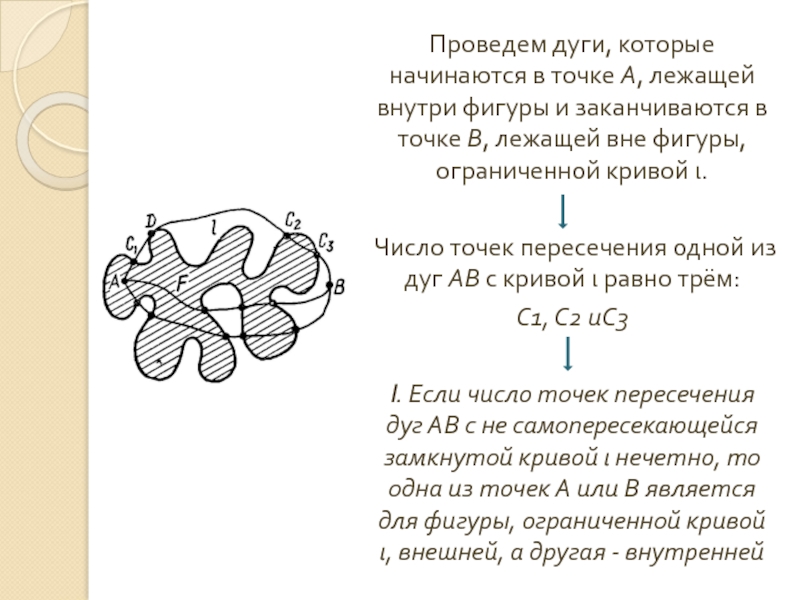
Слайд 18Проведем дуги, которые начинаются в точке А, лежащей внутри фигуры и
Число точек пересечения одной из дуг АВ с кривой ι равно трём:
С1, С2 иС3
I. Если число точек пересечения дуг АВ с не самопересекающейся замкнутой кривой ι нечетно, то одна из точек А или В является для фигуры, ограниченной кривой ι, внешней, а другая - внутренней
Слайд 19
ВНЕШНЯЯ ТОЧКА – если число точек пересечения луча, исходящего из данной
ВНУТРЕННЯЯ ТОЧКА - если число точек пересечения луча, исходящего из данной точки с не самопересекающейся прямой ι нечетно.
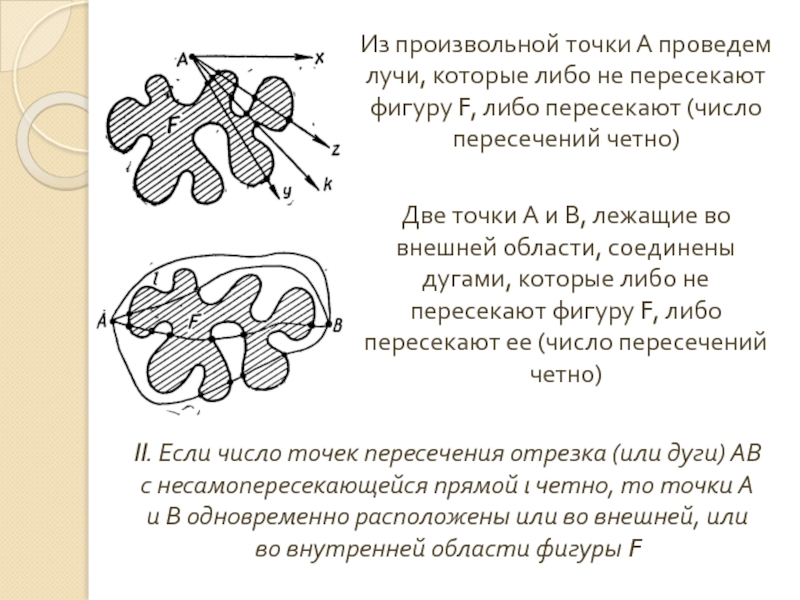
Слайд 20Из произвольной точки А проведем лучи, которые либо не пересекают фигуру
Две точки А и В, лежащие во внешней области, соединены дугами, которые либо не пересекают фигуру F, либо пересекают ее (число пересечений четно)
II. Если число точек пересечения отрезка (или дуги) АВ с несамопересекающейся прямой ι четно, то точки А и В одновременно расположены или во внешней, или во внутренней области фигуры F
Слайд 21РЕШЕНИЕ ЗАДАЧ
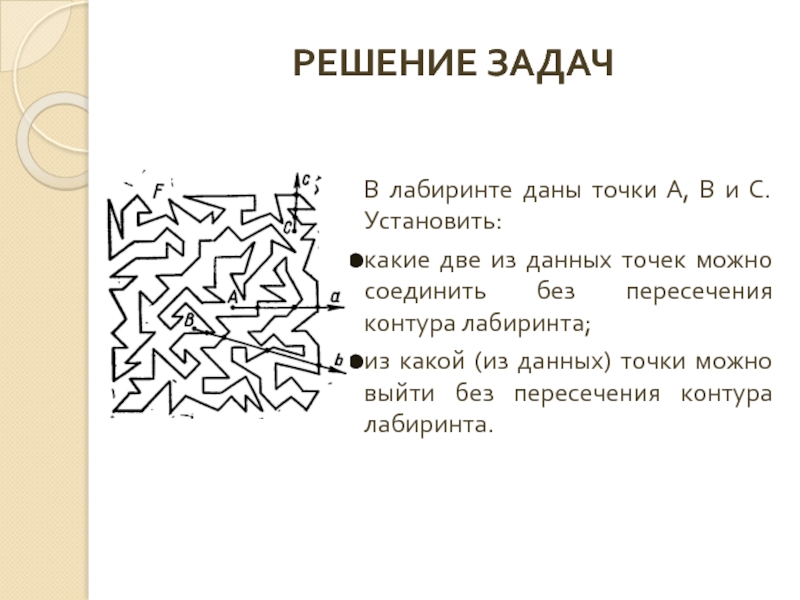
В лабиринте даны точки А, В и С. Установить:
какие две
из какой (из данных) точки можно выйти без пересечения контура лабиринта.
Слайд 22РЕШЕНИЕ ЗАДАНИЯ № 1:
Выясним в какой области находится каждая их этих
Лучи а и с пересекают его нечетное число раз, а луч в – четное. Согласно свойству №1 – точки А и С находятся в одной области, а точки А и В, В и С – в разных областях лабиринта.
Только точки А и С можно соединить, не пересекая контур лабиринта
Слайд 23РЕШЕНИЕ ЗАДАНИЯ № 2:
Определяем какие из этих точек лежат во внешней
Согласно свойству № 2, точка В лежит во внешней области, т.к. луч, проведенный из этой точки, пересекает контур четное число раз.
Значит из точки В можно выйти, не пересекая лабиринт.
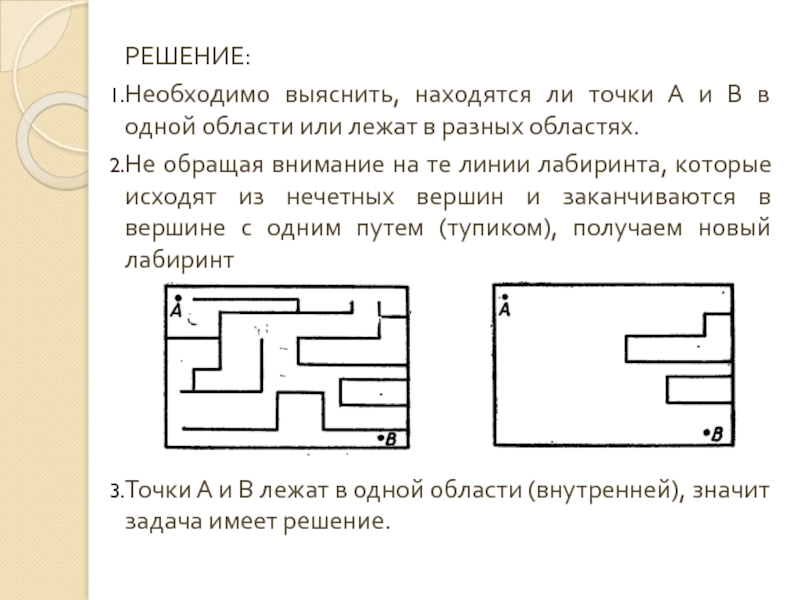
Слайд 25РЕШЕНИЕ:
Необходимо выяснить, находятся ли точки А и В в одной области
Не обращая внимание на те линии лабиринта, которые исходят из нечетных вершин и заканчиваются в вершине с одним путем (тупиком), получаем новый лабиринт
Точки А и В лежат в одной области (внутренней), значит задача имеет решение.
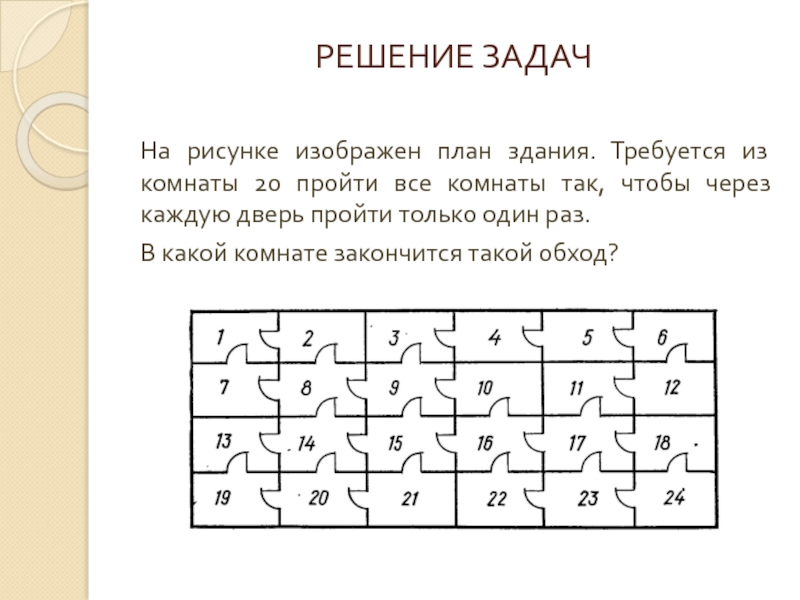
Слайд 26РЕШЕНИЕ ЗАДАЧ
На рисунке изображен план здания. Требуется из комнаты 20 пройти
В какой комнате закончится такой обход?
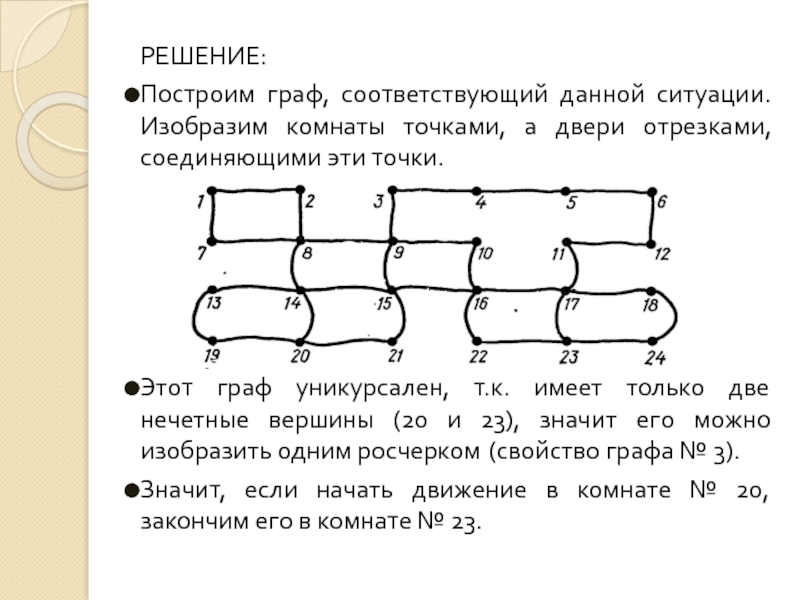
Слайд 27РЕШЕНИЕ:
Построим граф, соответствующий данной ситуации. Изобразим комнаты точками, а двери отрезками,
Этот граф уникурсален, т.к. имеет только две нечетные вершины (20 и 23), значит его можно изобразить одним росчерком (свойство графа № 3).
Значит, если начать движение в комнате № 20, закончим его в комнате № 23.
Слайд 29Решение:
В лабиринте имеются запутывающие искусственные линии, т.к. заведомо известно, что такой
Во время такого движения мы прошли ненужные отрезки пути. Попробуем отыскать относительно эффективный путь. Для этого при возвращении из тупика необходимо пройти так, чтобы при выходе из него образовалась петля, которая, как и все другие петли, будет означать ненужный путь. Идя второй раз, минуя образовавшиеся петли, получим путь более короткий.