- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по начертательной геометрии Урок№2 Трёхкартинный комплексный чертёж
Содержание
- 1. Презентация по начертательной геометрии Урок№2 Трёхкартинный комплексный чертёж
- 2. при разворачиванииплоскостей проекций все три поля оказываются
- 3. VHWVHWПРИМЕРЫ ПОСТРОЕНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА ТОЧКИ Существует
- 4. Построение недостающей проекцииПостроение недостающей проекцииПо условию заданы
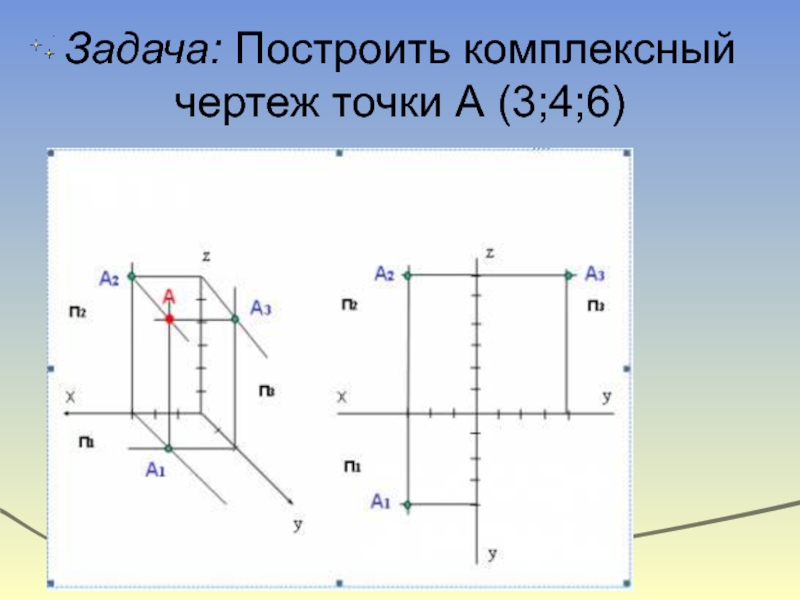
- 5. Задача: Построить комплексный чертеж точки А (3;4;6)
- 6. Пример. Построить комплексный чертеж точки А, удаленной
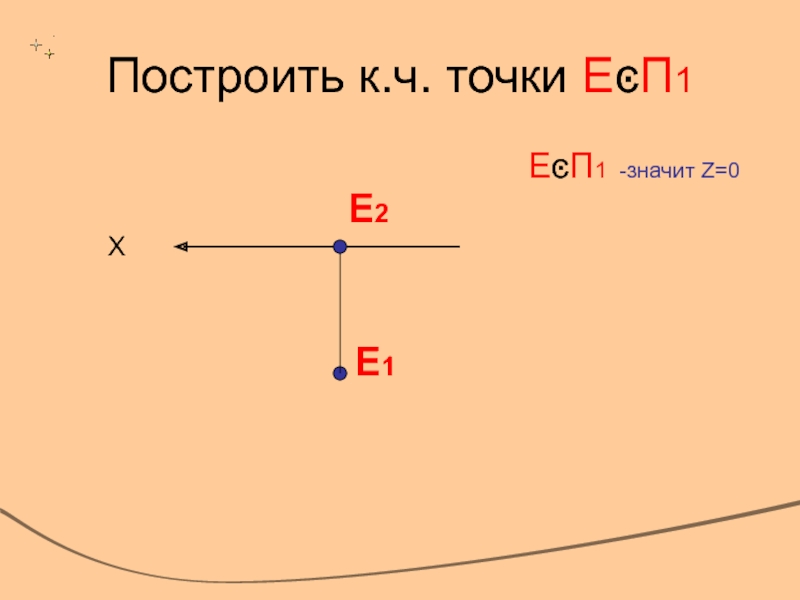
- 7. Построить к.ч. точки ЕͼП1ЕͼП1 -значит Z=0ΧЕ2Е1
- 8. Классификация точек в пространстве Пространственная точка А
- 9. Если две координаты точки = 0, то
- 10. октанты Введённая система трёх плоскостей П1,П2,П3-разбивает
- 11. При выполнении чертежей и решении задач не
- 12. Вопросы для повторения: 1. Что такое октанты?
- 13. Тренинг Ответ:2. Точка А,
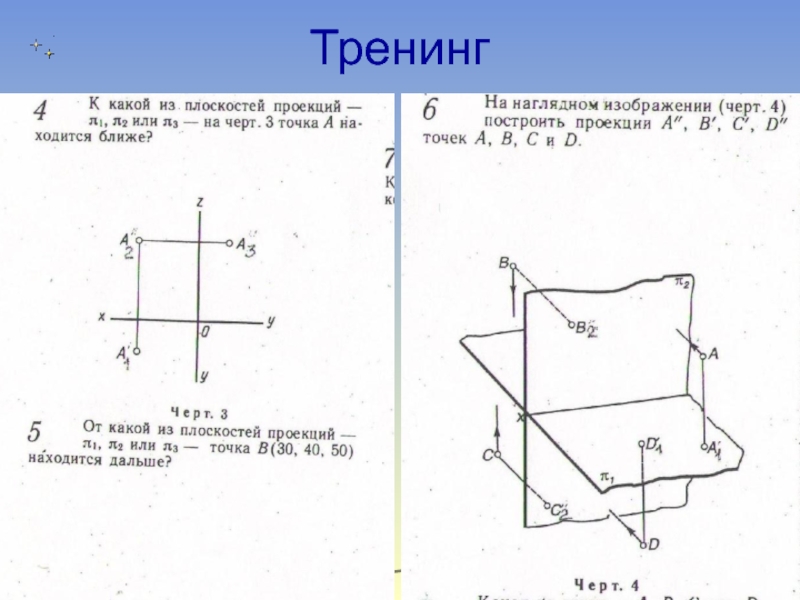
- 14. Тренинг
- 15. Слайд 15
- 16. Слайд 16
- 17. Слайд 17
- 18. Домашнее задание: Задание№1 стр23 (пособие) Задачи1-7Желаю успехов
Слайд 1Урок №2
трёхкартинный комплексный
чертёж
Самарский медико-технический лицей
*
УЧИТЕЛЬ ЧЕРЧЕНИЯ И ИЗОБРАЗИТЕЛЬНОГО ИСКУССТВА КАДИЛКИНА
Слайд 2при разворачивании
плоскостей проекций все три поля оказываются в плоскости П2
наглядное изображение
при
плоскостей проекций все три поля оказываются в плоскости П2
Слайд 3V
H
W
V
H
W
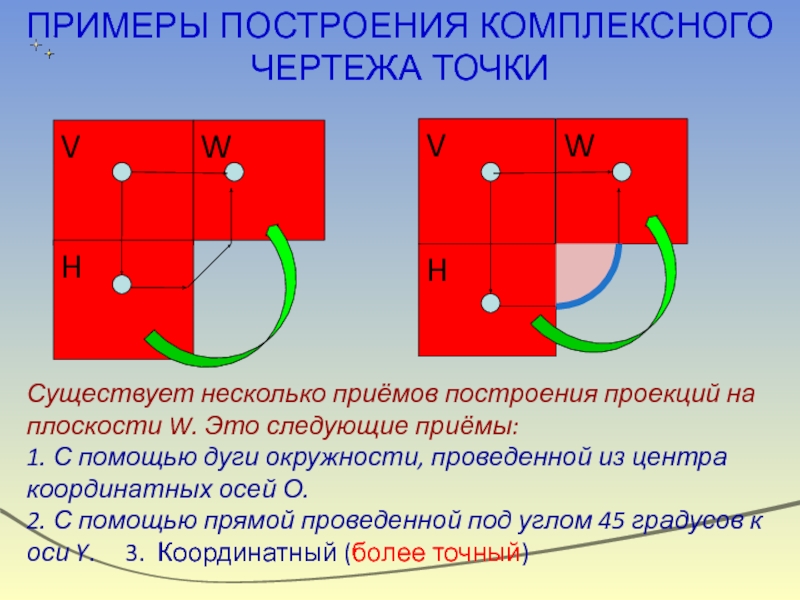
ПРИМЕРЫ ПОСТРОЕНИЯ КОМПЛЕКСНОГО ЧЕРТЕЖА ТОЧКИ
Существует несколько приёмов построения проекций
1. С помощью дуги окружности, проведенной из центра координатных осей О.
2. С помощью прямой проведенной под углом 45 градусов к оси Y. 3. Координатный (более точный)
Слайд 4Построение недостающей проекции
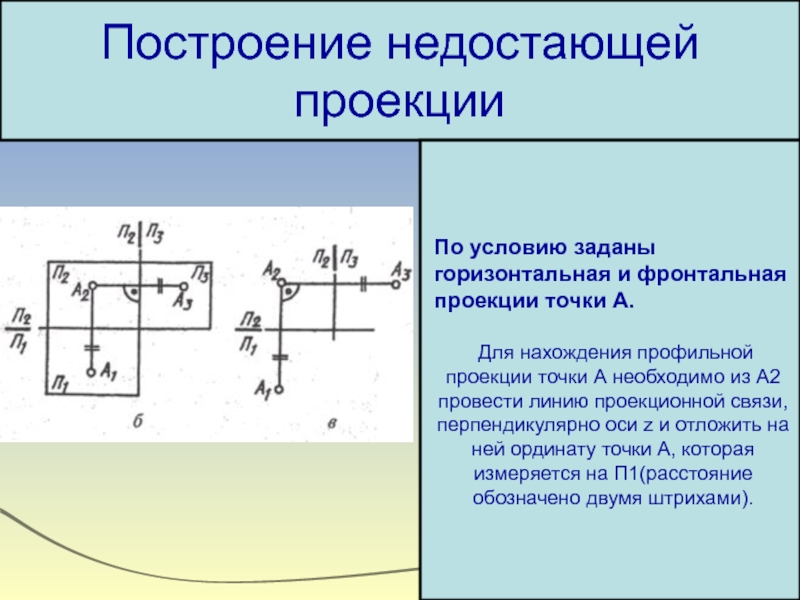
Построение недостающей проекции
По условию заданы горизонтальная и фронтальная проекции
Для нахождения профильной проекции точки А необходимо из А2 провести линию проекционной связи, перпендикулярно оси z и отложить на ней ординату точки А, которая измеряется на П1(расстояние обозначено двумя штрихами).
Слайд 6
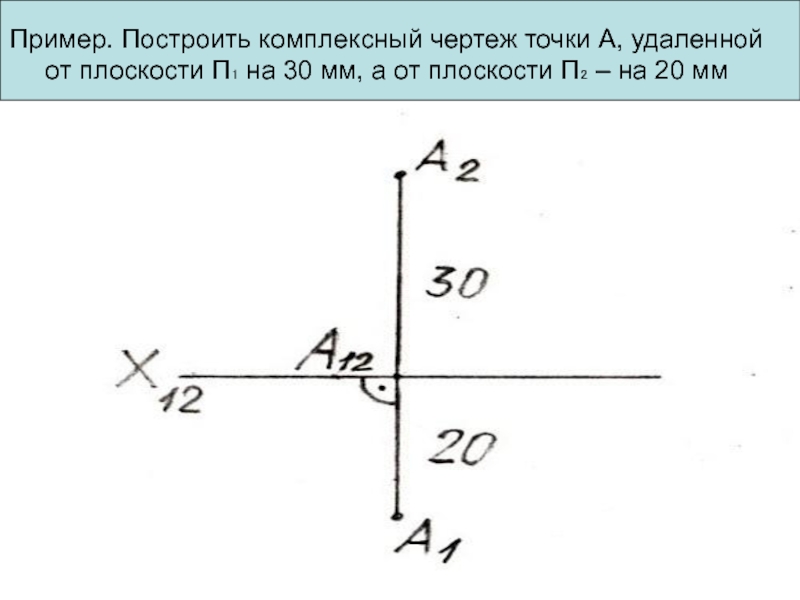
Пример. Построить комплексный чертеж точки А, удаленной от плоскости П₁ на
Слайд 8Классификация точек в пространстве
Пространственная точка А находится (∈) в пространстве R,
Если одна из координат = 0, а остальные не равны, то в общем случае точка принадлежит плоскости проекций. Так, если:
1. Х = 0, а Y, Z ≠ 0, то точка принадлежит профильной плоскости проекций.
2. Y = 0, а X, Z ≠ 0, то точка принадлежит фронтальной плоскости проекций.
3. Z = 0, а X, Y ≠ 0, то точка принадлежит горизонтальной плоскости проекций.
Слайд 9Если две координаты точки = 0, то точка находится на оси.
Так,
1. Y, Z = 0, а X ≠ 0, то точка находится на оси X,
2. X, Z = 0, а Y ≠ 0, то точка находится на оси Y,
3. Х, Y = 0, а Z ≠ 0, то точка находится на оси Z
Когда точка лежит в начале координат О – (ориго - начало, лат.), то все ее координаты равны 0.
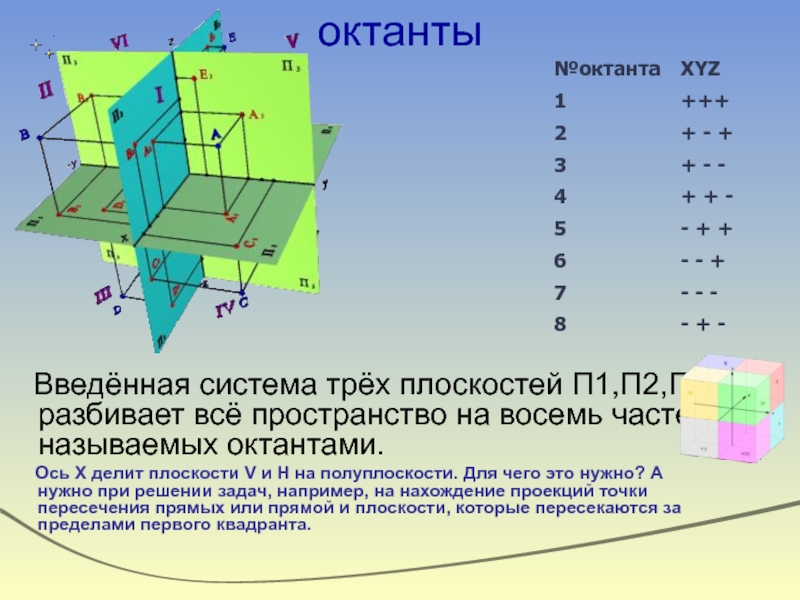
Слайд 10октанты
Введённая система трёх плоскостей П1,П2,П3-разбивает всё пространство на восемь
Ось Х делит плоскости V и H на полуплоскости. Для чего это нужно? А нужно при решении задач, например, на нахождение проекций точки пересечения прямых или прямой и плоскости, которые пересекаются за пределами первого квадранта.
Слайд 11При выполнении чертежей и решении задач не всегда нужна третья проекция,
Утром у подножия горы три внимательных альпиниста нашли одного невнимательного
Слайд 12Вопросы для повторения: 1. Что такое октанты? 2. В каком октанте значение координат
Вопросы для повторения:
1. Что такое октанты?
2. В каком октанте значение координат по всем осям имеет отрицательное значение?
3. Что такое прямоугольные координаты точки, и в какой последовательности их записывают в обозначении точки?
Примерные метрические задания:
1. В каком октанте будет находиться точка А, если имеет следующие координаты(20;-10;30)?
2. В каком октанте будет находиться точка В, если имеет следующие координаты (-20;10;-30)? Постойте эпюр Монжа для этой точки.
Ответ: во 2 октанте.
Ответ: находится в 8 октанте
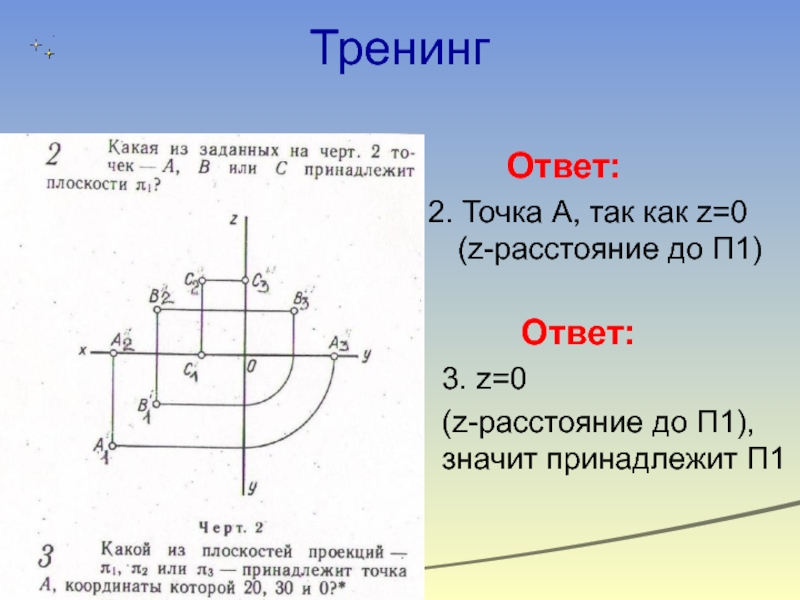
Слайд 13Тренинг
Ответ:
2. Точка А, так как z=0 (z-расстояние
Ответ:
3. z=0
(z-расстояние до П1), значит принадлежит П1