- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Правильные многогранники
Содержание
- 1. Презентация по математике Правильные многогранники
- 2. Правильных многогранников вызывающе мало, но этот весьма
- 3. Определение многогранника Многогранник
- 4. Многогранник называется правильным, если: 1) он выпуклый;
- 5. Сколько существует видов правильных многогранников?
- 6. Начала Евклида.
- 7. ПлатонПлатоновыми телами называются правильные однородные выпуклые многогранники.
- 8. Правильные многогранники занимают видное место в идеалистической
- 9. Олицетворение многогранниковТетраэдр олицетворял огонь, поскольку его вершина
- 10. Олицетворение многогранников Додекаэдр символизировал всё
- 11. пришли из Древней Греции, в них указывается
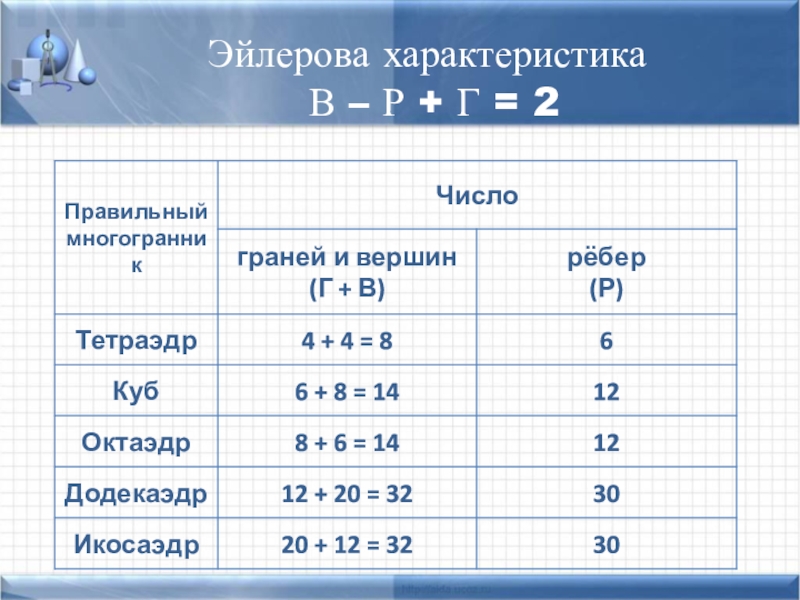
- 12. Эйлерова характеристика В – Р + Г = 2
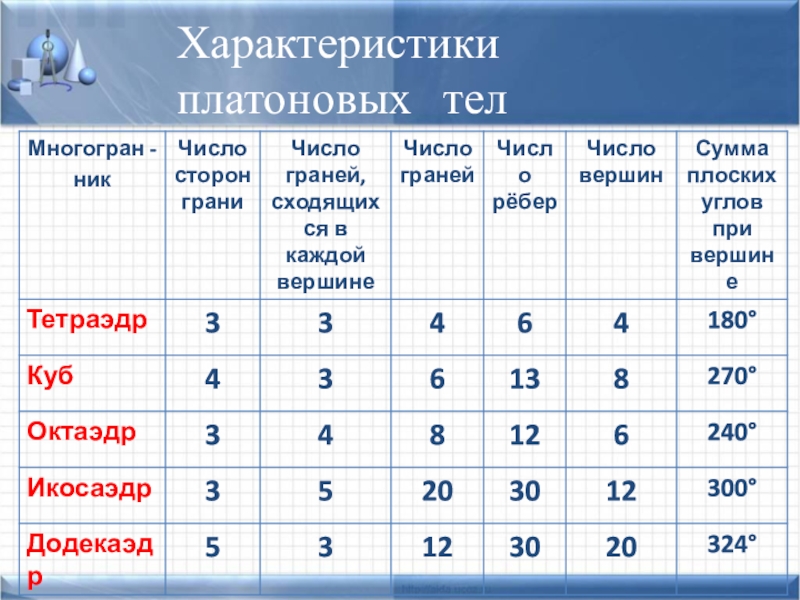
- 13. Характеристики платоновых тел
- 14. Архимед СиракузскийМатематик, физик и инженер Архимед Сиракузский
- 15. Немецкий астроном и математик. Один
- 16. «Космический кубок» Кеплера Кеплер
- 17. Идеи Платона и
- 18. Правильные многогранники и природа
- 19. Правильные многогранники – самые «выгодные» фигуры. И
- 20. При производстве алюминия пользуются алюминиево-калиевыми кварцами (K[Al(SO4)2]
- 21. В разных химических реакциях применяется сурьменистый сернокислый
- 22. Дюрер. Меланхолия
- 23. Сальвадор Дали«Тайная вечеря»
- 24. ГРАВЮРА ГОЛАНДСКОГО ХУДОЖНИКА МАУРИЦА КОРНЕЛИУСА ЭШЕРА «СИЛЫ ГРАВИТАЦИИ»
- 25. Правильный многогранник, у которого грани правильные треугольники
- 26. ОКТАЭДРПравильный многогранник, у которого грани- правильные
- 27. ИКОСОЭДРПравильный многогранник, у которого грани - правильные
- 28. КУБ -правильный многогранник, у которого грани –
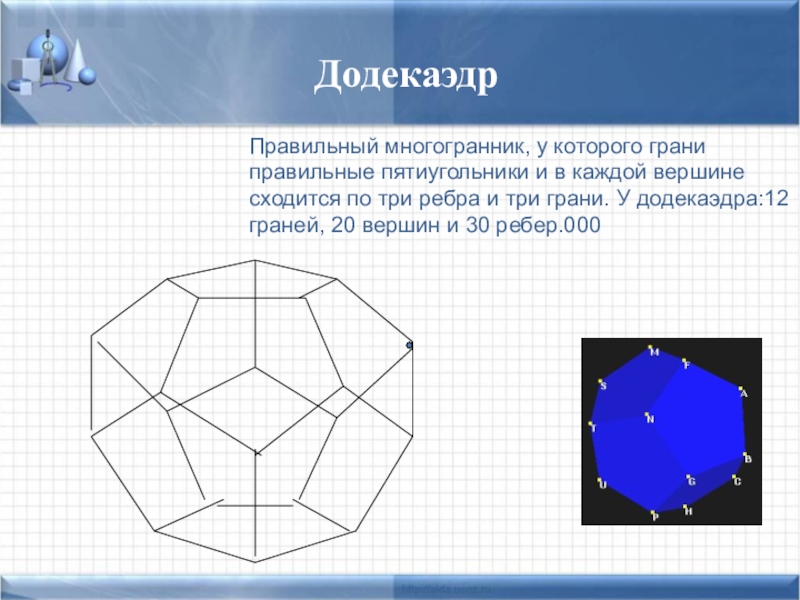
- 29. Правильный многогранник, у которого грани правильные пятиугольники
- 30. Слайд 30
- 31. http://www.uni-giessen.de/~g013/polyhedron_movies/dual/ikosa-dodeka/index.html http://irkschool31.ucoz.ru/mathematika/mnogogranniki/5-cell.gif
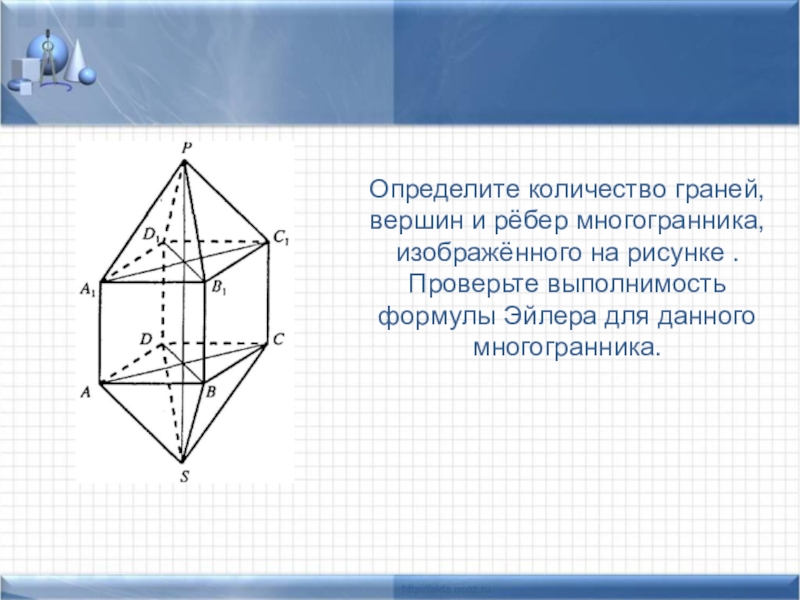
- 32. Определите количество граней, вершин и рёбер многогранника,
Слайд 1Правильные многогранники
геометрия 11 класс
Теленгатор С.В. учитель математики
МОУ Лицей №15 им.
Саров - 2011г.
Слайд 2Правильных многогранников вызывающе мало, но этот весьма скромный по численности отряд
Л. Кэрролл
Слайд 3Определение многогранника
Многогранник – это часть пространства,
Слайд 4Многогранник называется правильным, если: 1) он выпуклый; 2) все его грани
Примером правильного многогранника является куб, тетраэдр
Определение правильного
многогранника
Слайд 6 Начала Евклида. «В геометрии нет
Главный труд Евклида – «Начала» (в оригинале «Стохейа». «Начала» состоят из 13 книг, позднее к ним были прибавлены ещё 2.
Первые шесть книг посвящены планиметрии. Книги VII – X содержат теорию чисел, XI, XII и XIII книги «Начал» посвящены стереометрии.
Из постулатов Евклида видно, что он представлял пространство как пустое, безграничное, изотропное и трёхмерное.
Интересно, что «Начала» Евклида открываются описанием построения правильного треугольника и заканчиваются изучением пяти правильных многогранных тел! В наше время они известны как платоновы тела.
около 365 – 300 гг. до н.э.
Слайд 7Платон
Платоновыми телами называются правильные однородные выпуклые многогранники.
Платоновы тела - трехмерный
Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида.
около 429 – 347 г.г. до н.э.
Слайд 8Правильные многогранники занимают видное место в идеалистической картине мира древнегреческого философа
Платон
Изучение многогранников на протяжении всей истории велось не только с позиций дальнейшего их применения, но и с целью осмысления философских вопросов об устройстве Вселенной и природе, пространства.
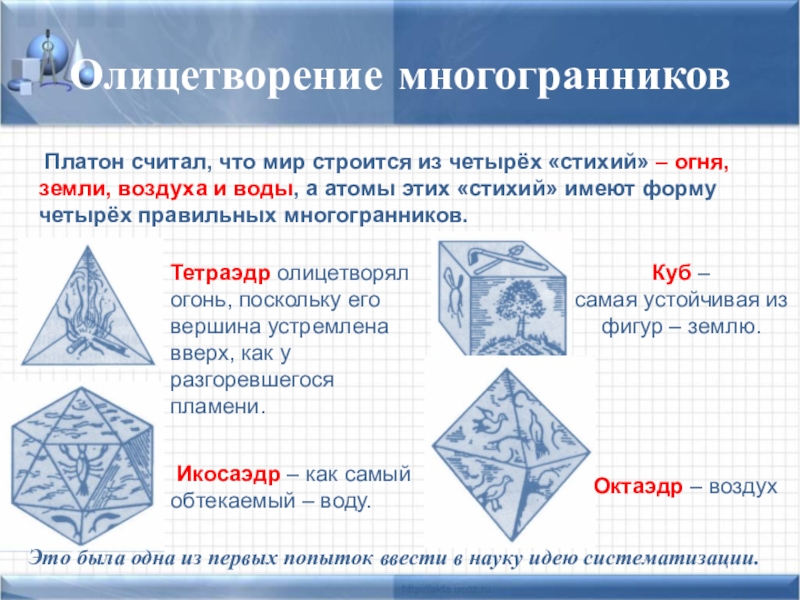
Слайд 9Олицетворение многогранников
Тетраэдр олицетворял огонь, поскольку его вершина устремлена вверх, как у
Куб –
самая устойчивая из фигур – землю.
Октаэдр – воздух
Икосаэдр – как самый обтекаемый – воду.
Это была одна из первых попыток ввести в науку идею систематизации.
Платон считал, что мир строится из четырёх «стихий» – огня, земли, воздуха и воды, а атомы этих «стихий» имеют форму четырёх правильных многогранников.
Слайд 10Олицетворение многогранников
Додекаэдр символизировал всё мироздание, почитался главнейшим. Уже
Слайд 11пришли из Древней Греции,
в них указывается число граней:
«эдра» −
«тетра» − 4;
«гекса» − 6;
«окта» − 8;
«икоса» − 20;
«додека» − 12.
Названия многогранников
Слайд 14Архимед Сиракузский
Математик, физик и инженер Архимед Сиракузский оставил после себя немало
Архимед, как геометр определил поверхность шара и его объём, исследовал параболоиды и гиперболоиды, изучал «архимедову спираль», определил число «пи», как находящееся между 3,141 и 3,142.
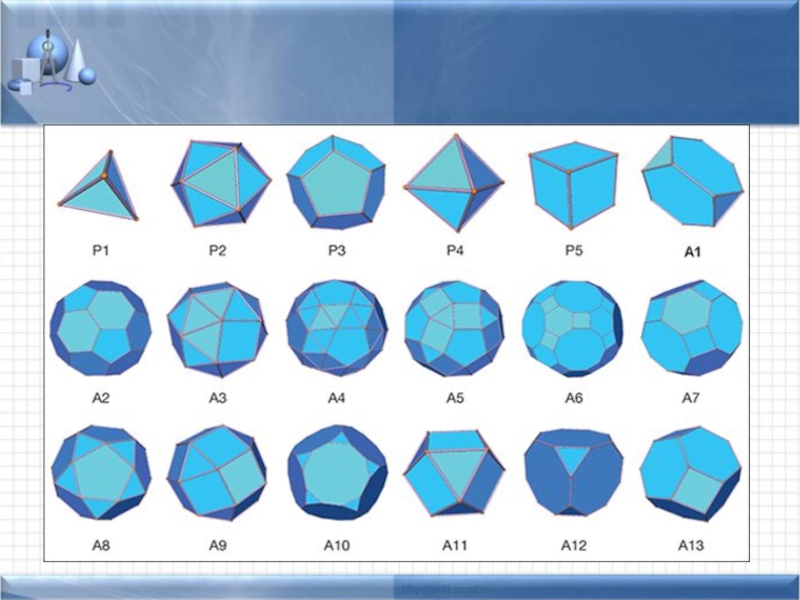
Вклад Архимеда в теорию многогранников - описание 13 полуправильных выпуклых однородных многогранников (архимедовых тел).
около 287 – 212 гг. до н.э.
Слайд 15 Немецкий астроном и математик. Один из создателей современной астрономии.
Вклад Кеплера в теорию многогранника - это, во-первых, восстановление математического содержания утерянного трактата Архимеда о полуправильных выпуклых однородных многогранниках.
Еще более существенным было предложение Кеплера рассматривать невыпуклые многогранники со звездчатыми гранями, подобными пентаграмме и последовавшее за этим открытие двух правильных невыпуклых однородных многогранников - малого звездчатого додекаэдра и большого звездчатого додекаэдра.
1571 – 1630 гг.
Иоганн Кеплер
Слайд 16«Космический кубок» Кеплера
Кеплер предположил, что существует связь
Согласно этому предположению, в сферу орбиты Сатурна можно вписать куб, в который вписывается сфера орбиты Юпитера. В неё, в свою очередь, вписывается тетраэдр, описанный около сферы орбиты Марса. В сферу орбиты Марса вписывается додекаэдр, к который вписывается сфера орбиты Земли. А она описана около икосаэдра, в который вписана сфера орбиты Венеры. Сфера этой планеты описана около октаэдра, в который вписывается сфера Меркурия.
Такая модель Солнечной системы (рис. 6) получила название «Космического кубка» Кеплера. Результаты своих вычислений учёный опубликовал в книге «Тайна мироздания». Он считал, что тайна Вселенной раскрыта.
Год за годом учёный уточнял свои наблюдения, перепроверял данные коллег, но, наконец, нашёл в себе силы отказаться от заманчивой гипотезы. Однако её следы просматриваются в третьем законе Кеплера, где говориться о кубах средних расстояний от Солнца.
Модель Солнечной
системы И. Кеплера
Слайд 17 Идеи Платона и Кеплера о связи правильных
Многие залежи полезных ископаемых тянутся вдоль икосаэдро-додекаэдровой сетки; 62 вершины и середины рёбер многогранников, называемых авторами узлами, обладают рядом специфических свойств, позволяющих объяснить некоторые непонятные явления. Здесь располагаются очаги древнейших культур и цивилизаций: Перу, Северная Монголия, Гаити, Обская культура и другие. В этих точках наблюдаются максимумы и минимумы атмосферного давления, гигантские завихрения Мирового океана. В этих узлах находятся озеро Лох-Несс, Бермудский треугольник.
Дальнейшие исследования Земли, возможно, определят отношение к этой научной гипотезе, в которой, как видно, правильные многогранники занимают важное место.
Икосаэдро-додекаэдровая
структура Земли
Слайд 18Правильные многогранники и природа
Правильные многогранники встречаются в
Чем же вызвана такая природная геометризация феодарий? По-видимому, тем, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объём при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.
Слайд 19Правильные многогранники – самые «выгодные» фигуры. И природа этим широко пользуется.
Взять хотя бы поваренную соль, без которой мы не можем обойтись. Известно, что она растворима в воде, служит проводником электрического тока. А кристаллы поваренной соли (NaCl) имеют форму куба.
Правильные многогранники и природа
Слайд 20При производстве алюминия пользуются алюминиево-калиевыми кварцами (K[Al(SO4)2] ⋅ 12H2O), монокристалл которых
Получение серной кислоты, железа, особых сортов цемента не обходится без сернистого колчедана (FeS). Кристаллы этого химического вещества имеют форму додекаэдра.
Правильные многогранники и природа
Слайд 21В разных химических реакциях применяется сурьменистый сернокислый натрий (Na5(SbO4(SO4)) – вещество,
Последний правильный многогранник – икосаэдр передаёт форму кристаллов бора (В). В своё время бор использовался для создания полупроводников первого поколения.
Правильные многогранники и природа
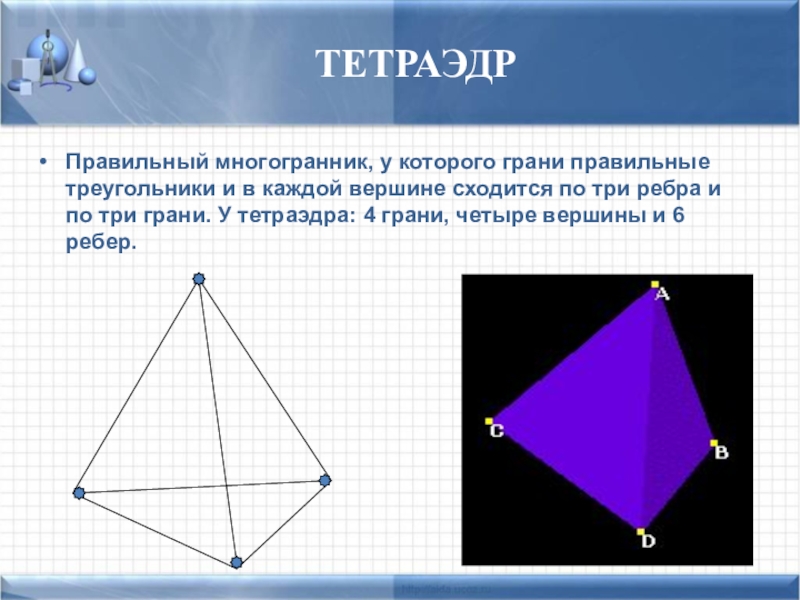
Слайд 25Правильный многогранник, у которого грани правильные треугольники и в каждой вершине
ТЕТРАЭДР
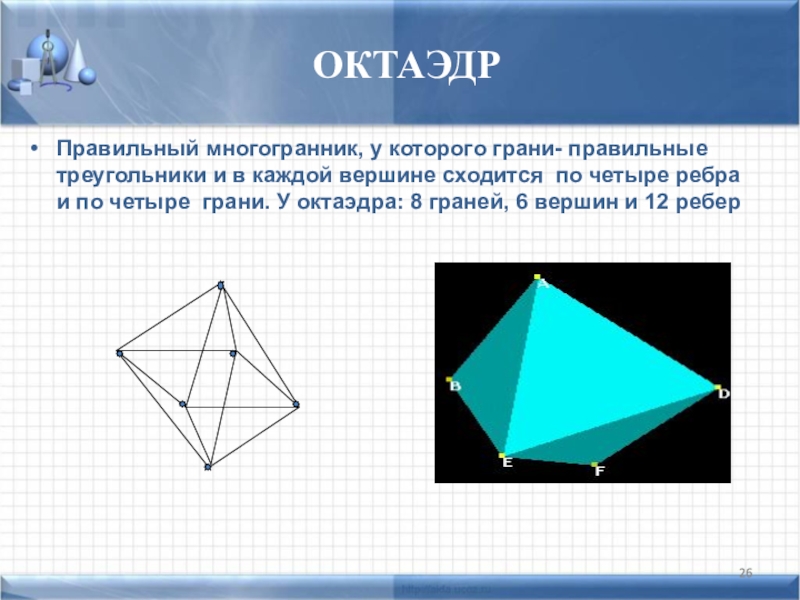
Слайд 26 ОКТАЭДР
Правильный многогранник, у которого грани- правильные треугольники и в каждой
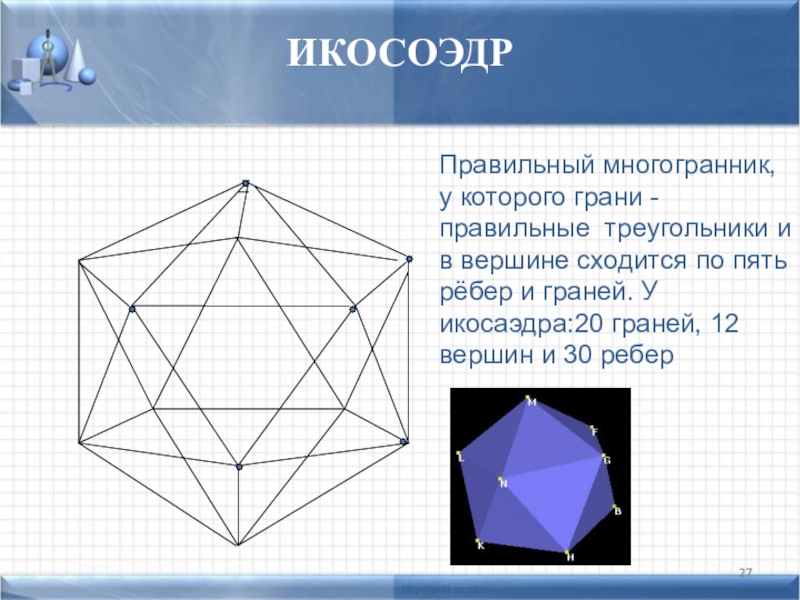
Слайд 27ИКОСОЭДР
Правильный многогранник, у которого грани - правильные треугольники и в вершине
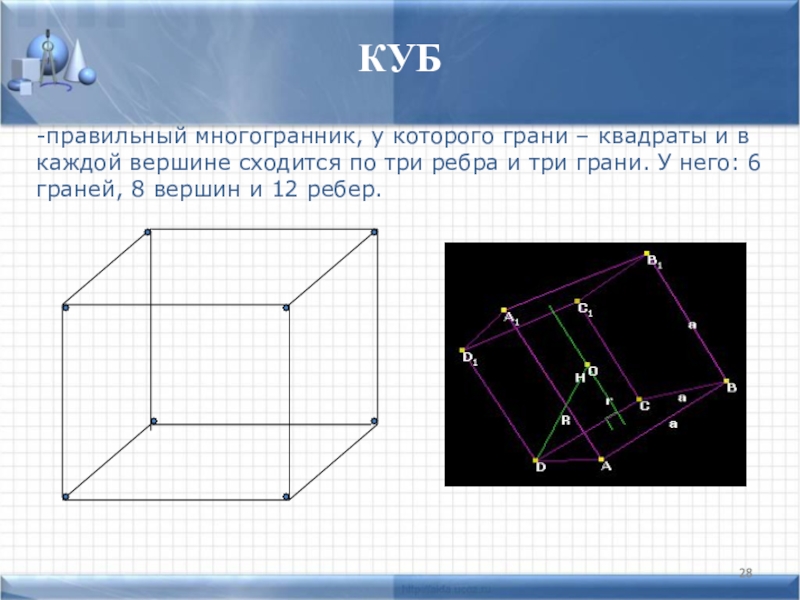
Слайд 28КУБ
-правильный многогранник, у которого грани – квадраты и в каждой
Слайд 29
Правильный многогранник, у которого грани правильные пятиугольники и в каждой вершине
Додекаэдр
















![Презентация по математике Правильные многогранники При производстве алюминия пользуются алюминиево-калиевыми кварцами (K[Al(SO4)2] ⋅ 12H2O), монокристалл которых При производстве алюминия пользуются алюминиево-калиевыми кварцами (K[Al(SO4)2] ⋅ 12H2O), монокристалл которых имеет форму правильного октаэдра.Получение серной кислоты,](/img/thumbs/f8c926d6ff7255d6cc9a4a74dd305c86-800x.jpg)