промышленно-гуманитарный техникум имени А.В. Яковлева»
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике Площадь криволинейной трапеции
Содержание
- 1. Презентация по математике Площадь криволинейной трапеции
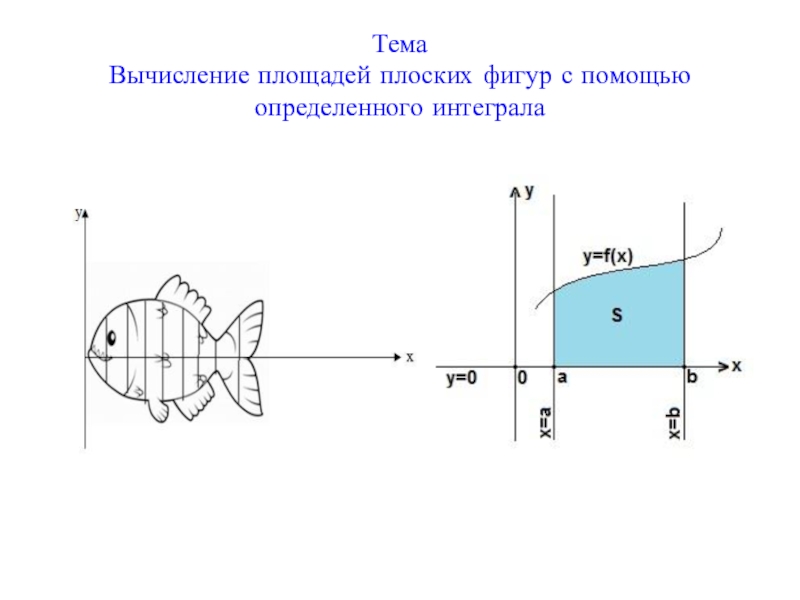
- 2. Тема Вычисление площадей плоских фигур с помощью определенного интеграла
- 3. Математический диктантУ= sin xY = cos xY
- 4. Ответы(sin x)/ =cos x (cos x)/ =
- 5. Применение производной к решению задачСоставить уравнение касательной к графику дифференцируемой в точке х0 функции f(x)
- 6. Решение Вариант 1f (х0) = 5f /
- 7. Решение Вариант 2f (х0) = - 8f
- 8. Таблица первообразных
- 9. Текущее повторение Вычислите определенный интегралМордкович А.Г. Алгебра и начала математического анализаЗадачник, с. 133, № 21.7(а,б)
- 10. Физкультурная пауза
- 11. Определение Фигура, ограниченная осью х, прямыми х
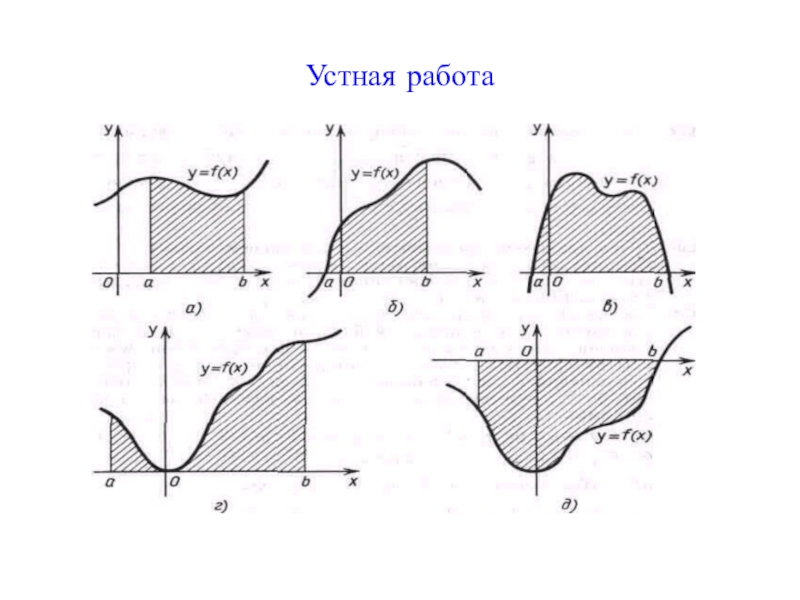
- 12. Устная работа
- 13. Устная работа
- 14. Ученые, внесшие вклад в развитие интегрального исчисления
- 15. Ученые, внесшие вклад в развитие интегрального исчисления
- 16. Формула Ньютона - ЛейбницаТеорема: Если функция у
- 17. Алгоритм решения задачи на вычисление площади криволинейной
- 18. Применение интеграла
- 19. ЗакреплениеВариант 1 № 21.43 (а)Вариант 2 №21.43 (в)
- 20. Домашнее заданиеА.Г.Мордкович Алгебра и начала математического анализа
Тема Вычисление площадей плоских фигур с помощью определенного интеграла
Слайд 1Министерство образования и науки Челябинской области государственное бюджетное профессиональное образовательное учреждение «Челябинский государственный
Слайд 3Математический диктант
У= sin x
Y = cos x
Y = tg x
Y =
ctg x
Y = e x
Y = ax
Y = ln x
Y = logax
Y = xn
Y =kx + b
Y = e x
Y = ax
Y = ln x
Y = logax
Y = xn
Y =kx + b
Слайд 4Ответы
(sin x)/ =cos x
(cos x)/ = - sin x
(tg x)/
= 1/ cos2 x
( ctg x)/ = - 1/ sin2x
(e x)/ = ex
( ax)/ = ax lna
(ln x)/ = 1/х
( logax)/ =1/х lna
(xn)/ =nxn - 1
(kx + b)/ =k
( ctg x)/ = - 1/ sin2x
(e x)/ = ex
( ax)/ = ax lna
(ln x)/ = 1/х
( logax)/ =1/х lna
(xn)/ =nxn - 1
(kx + b)/ =k
Слайд 5Применение производной к решению задач
Составить уравнение касательной к графику дифференцируемой в
точке х0
функции f(x)
функции f(x)
Слайд 6Решение
Вариант 1
f (х0) = 5
f / (x) = 2x + 3
f
/ (х0) = 3
Y = 5+ 3(x -0)
y = 5 + 3x
Ответ: y = 3x + 5
Y = 5+ 3(x -0)
y = 5 + 3x
Ответ: y = 3x + 5
Слайд 7Решение
Вариант 2
f (х0) = - 8
f / (x) = -2x +
6
f / (х0) = 10
Y = - 8+ 10(x + 2)
y = - 8 + 10x + 20
у = 10х + 12
Ответ: y = 10х + 12
f / (х0) = 10
Y = - 8+ 10(x + 2)
y = - 8 + 10x + 20
у = 10х + 12
Ответ: y = 10х + 12
Слайд 9Текущее повторение
Вычислите определенный интеграл
Мордкович А.Г.
Алгебра и начала математического анализа
Задачник, с.
133, № 21.7(а,б)
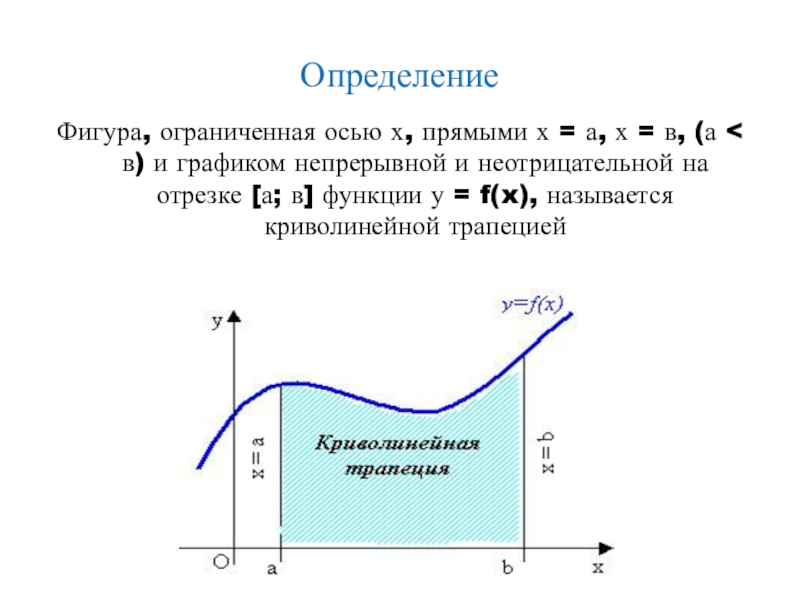
Слайд 11Определение
Фигура, ограниченная осью х, прямыми х = а, х =
в, (а < в) и графиком непрерывной и неотрицательной на отрезке [а; в] функции у = f(x), называется криволинейной трапецией
Слайд 16Формула Ньютона - Лейбница
Теорема:
Если функция у = f(x) непрерывна на
отрезке [а; в], то справедлива формула
b
∫ f(x)dx = F(b) – F(a)
a
b
∫ f(x)dx = F(b) – F(a)
a
![Формула Ньютона - ЛейбницаТеорема: Если функция у = f(x) непрерывна на отрезке [а; в], то справедлива формула](/img/thumbs/b916b76c66ae151b4dd30f921ff8dc7e-800x.jpg "Презентация по математике Площадь криволинейной трапеции Формула Ньютона - ЛейбницаТеорема: Если функция у = f(x) непрерывна на")
Слайд 17Алгоритм решения задачи на вычисление площади криволинейной трапеции
Построить в одной системе
координат заданные линии
Обозначить криволинейную трапецию
Найти первообразную подинтегральной функции у = f(x)
Осуществить двойную подстановку
Записать ответ
Обозначить криволинейную трапецию
Найти первообразную подинтегральной функции у = f(x)
Осуществить двойную подстановку
Записать ответ
Слайд 20Домашнее задание
А.Г.Мордкович
Алгебра и начала математического анализа 11 класс . Задачник,
п. 21, № 21.43(б), № 21.44(в)
