Перпендикулярность прямой и плоскости
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике: Перпендикулярность прямой и плоскости
Содержание
- 1. Презентация по математике: Перпендикулярность прямой и плоскости
- 2. Перпендикулярные прямые в пространстве
- 3. ЛеммаЕсли одна из двух параллельных прямых перпендикулярна
- 4. ОпределениеПрямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.аα
- 5. ТеоремаЕсли одна из двух параллельных прямыхперпендикулярна к
- 6. Обратная теоремаЕсли две прямые перпендикулярны к плоскости,
- 7. Признак перпендикулярности прямой и плоскостиЕсли прямая перпендикулярна
- 8. Теорема о прямой, перпендикулярной к плоскостиЧерез любую
- 9. ЗадачаВ треугольнике АВС ∠С = 90o, АС
- 10. Самостоятельная работа1 вариант
Перпендикулярные прямые в пространстве abсДве прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90o.Прямые a ┴ b пересекающиеся,прямые с
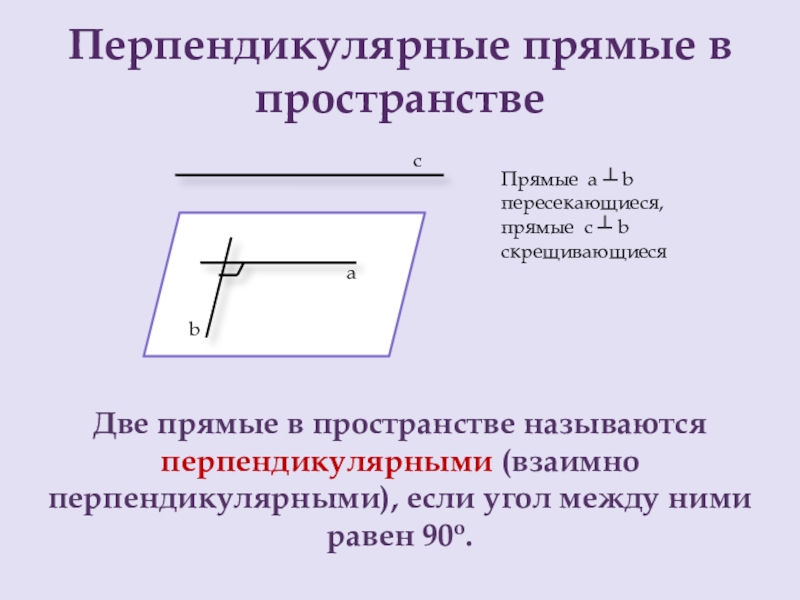
Слайд 2Перпендикулярные прямые в пространстве
a
b
с
Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90o.
Прямые a ┴ b пересекающиеся,
прямые с ┴ b скрещивающиеся
Слайд 3Лемма
Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то
и другая перпендикулярна к этой прямой.
А
С
М
Доказательство
Пусть а ║ b, a ┴ c. Докажем, что
b ┴ c.
Через произвольную точку М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные прямым
а и с. Так как а ┴ с, то ∠ МАС = 90o. По условию b║ a, а по построению а ║ МА, поэтому b ║ МА. Итак, прямые b и с параллельны прямым МА и МС, угол между которыми равен 90o. Это означает, что угол между прямыми b и с также равен 90o. Значит b ┴ с.
с
a
b
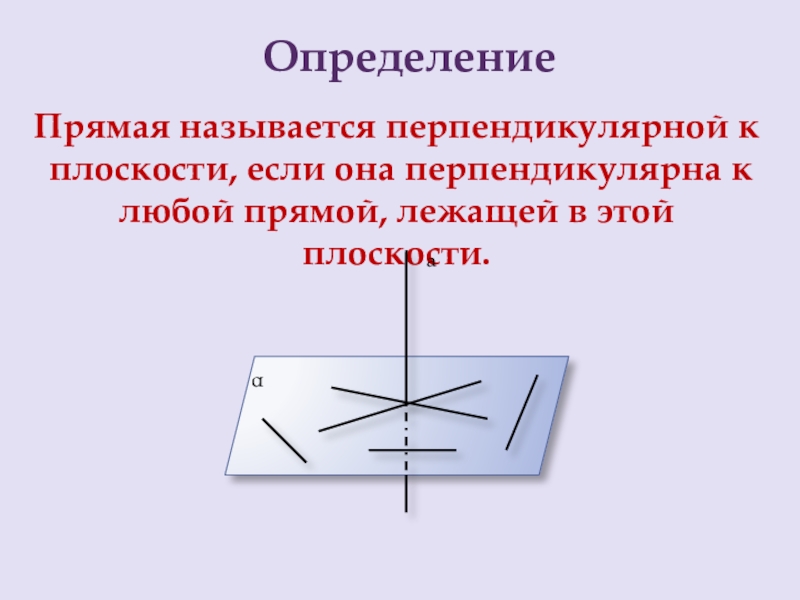
Слайд 4Определение
Прямая называется перпендикулярной к
плоскости, если она перпендикулярна к
любой прямой,
лежащей в этой плоскости.
а
α
Слайд 5Теорема
Если одна из двух параллельных прямых
перпендикулярна к плоскости, то и другая
прямая перпендикулярна к этой плоскости.
а а1
х
α
Доказательство
Рассмотрим прямые а ║ а1 и плоскость α,
такую, что а ┴ α. Докажем, что и а1 ┴ α.
Проведем какую - нибудь прямую х в плоскости α. Так как а ┴ α, то а ┴ х.
По лемме о перпендикулярности двух параллельных прямых к третьей а1 ┴ х.
Значит прямая а1 перпендикулярна к любой прямой, лежащей в плоскости α,
т. е а1 ┴ α. Что и требовалось доказать.
Слайд 6Обратная теорема
Если две прямые перпендикулярны к
плоскости, то они параллельны.
а b
α
Докажите самостоятельно
Слайд 7Признак перпендикулярности прямой и плоскости
Если прямая перпендикулярна к двум пересекающимся прямым,
лежащим в плоскости, то она перпендикулярна к этой плоскости.
Слайд 8Теорема о прямой, перпендикулярной к плоскости
Через любую точку пространства проходит
прямая,
перпендикулярная к данной плоскости, и притом только одна.
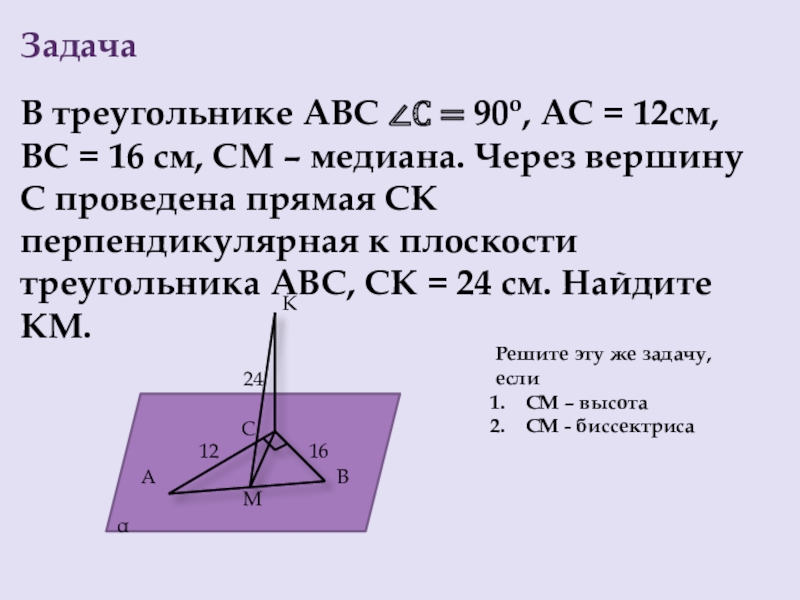
Слайд 9Задача
В треугольнике АВС ∠С = 90o, АС = 12см,
ВС =
16 см, СМ – медиана. Через вершину С проведена прямая СК перпендикулярная к плоскости треугольника АВС, СК = 24 см. Найдите КМ.
К
С
А В
α
24
12 16
М
Решите эту же задачу, если
СМ – высота
СМ - биссектриса
Слайд 10Самостоятельная работа
1 вариант
2 вариант
1. Прямая АВ ┴ α, М и К произвольные точки плоскости α. Докажите, что АВ ┴ МК.
2. ▲ АВС – правильный, точка О – его центр. Прямая ОМ перпендикулярна к плоскости АВС. Докажите, что
а) МА=МВ=МС.
б) Найдите МА, если
АВ=6 см, МО=2см.
1. Прямая МА перпендикулярна к плоскости треугольника АВС.
Докажите, что МА ┴ ВС.
2. АВСД – квадрат, точка О - его центр. Прямая ОМ перпендикулярна к плоскости квадрата.
а) Докажите, что
МА=МВ=МС=МД.
б) Найдите МА, если АВ=4см,
ОМ=1см.
4 см
3см
