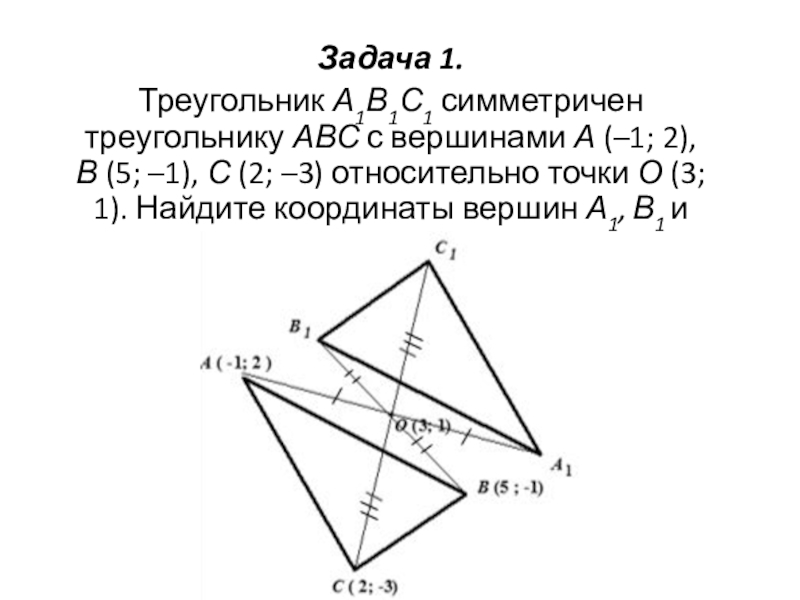
2), В (5; –1), С (2; –3) относительно точки О (3; 1). Найдите координаты вершин А1, В1 и С1.
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Задачи на движение
Содержание
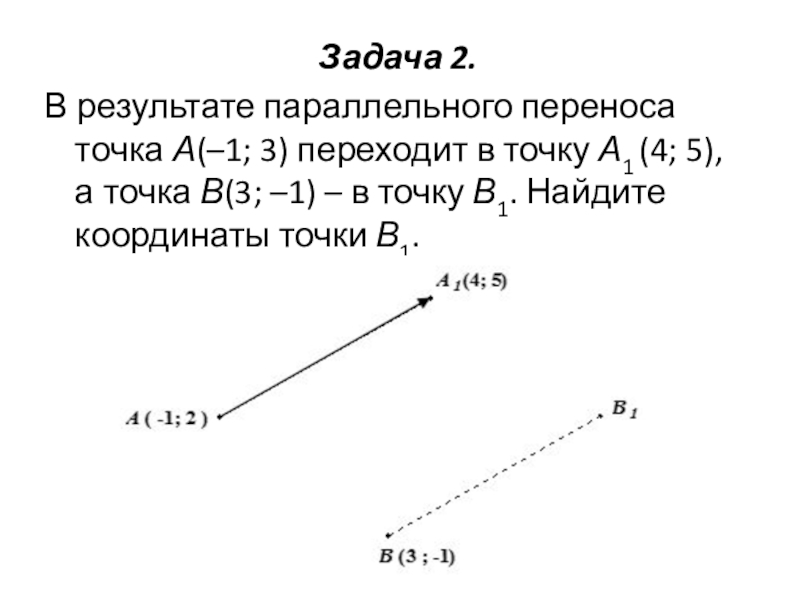
Задача 2. В результате параллельного переноса точка А(–1; 3) переходит в точку А1 (4; 5), а точка В(3; –1) – в точку В1. Найдите координаты точки В1.
Слайд 2Задача 2.
В результате параллельного переноса точка А(–1; 3) переходит в
точку А1 (4; 5), а точка В(3; –1) – в точку В1. Найдите координаты точки В1.
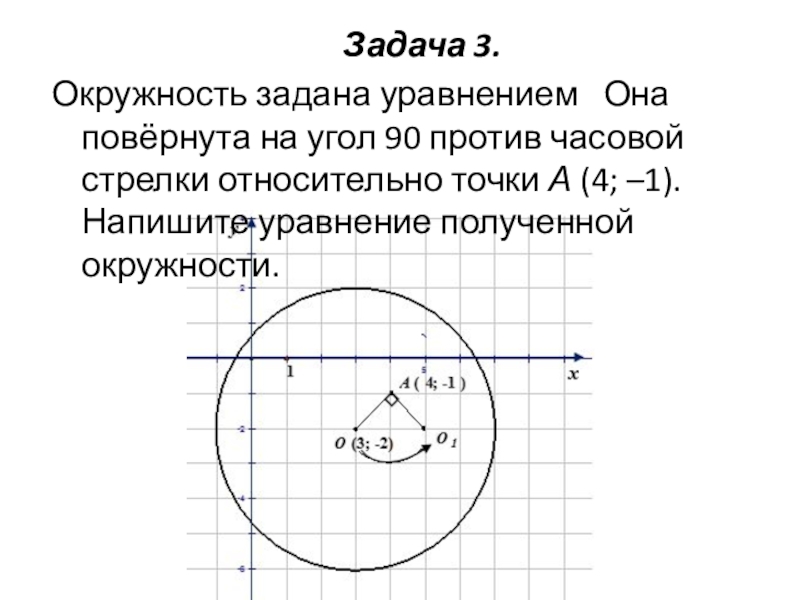
Слайд 3Задача 3.
Окружность задана уравнением Она повёрнута на угол 90 против
часовой стрелки относительно точки А (4; –1). Напишите уравнение полученной окружности.
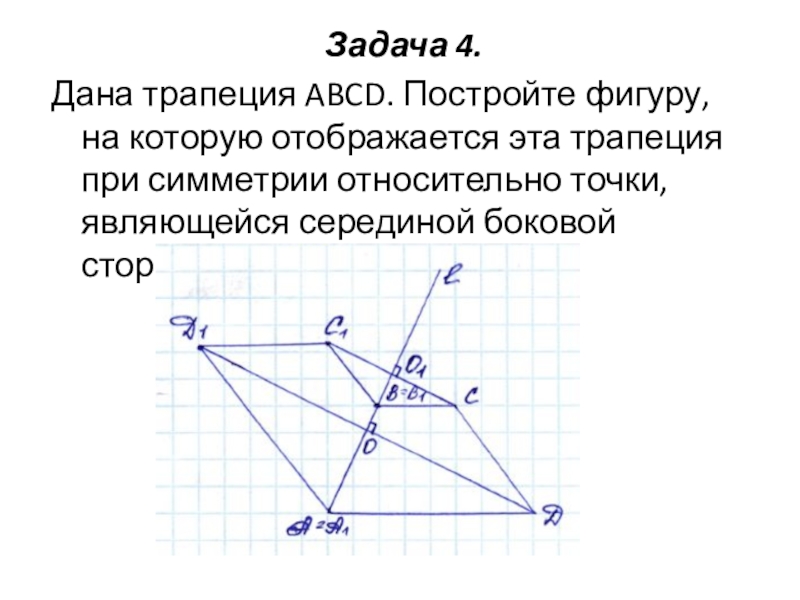
Слайд 4Задача 4.
Дана трапеция ABCD. Постройте фигуру, на которую отображается эта трапеция
при симметрии относительно точки, являющейся серединой боковой стороны CD.
Слайд 5Домашнее задание
На одной стороне угла ХОY отложены отрезки ОА и ОВ,
а на другой стороне – отрезки ОМ и ОN так, что ОМ = ОА, ОN = ОВ. Используя осевую симметрию, докажите, что точка пересечения отрезков МВ и АN лежит на биссектрисе угла ХОY.
Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно точки, являющейся серединой боковой стороны СD.
Дана трапеция АВСD. Постройте фигуру, на которую отображается эта трапеция при симметрии относительно точки, являющейся серединой боковой стороны СD.