- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Тетраэдр и параллелепипед. (10 класс)
Содержание
- 1. Презентация по математике на тему Тетраэдр и параллелепипед. (10 класс)
- 2. Многоугольник – часть плоскости, ограниченная линией, включая
- 3. Тетраэдр.Рассмотрим произвольный треугольник АBC и точку D, не лежащую в плоскости этого треугольника. ABCD
- 4. Соединим точку D отрезками с вершинами треугольника.ABCDПоверхность,
- 5. Треугольники, из которых состоит тетраэдр, называются гранями,
- 6. DBCA1) Назовите грани тетраэдраABC, ADC, CDB, ADB2)
- 7. Задачи на построение сечения в тетраэдре.Секущей плоскостью
- 8. Обязательные условия для задач на построение сечений.Отрезок
- 9. Задача:На рёбрах AB, BD и CD тетраэдра
- 10. DCABMNPДано: ABCD – тетраэдр
- 11. DCABMNPРешение:1)Построим прямую, по которой (MNP) пересекается с
- 12. Параллелепипед.Рассмотрим два равных параллелограмма ABCD и A1B1C1D1Расположенных
- 13. Поверхность, составленная из двух равных параллелограммов ABCD
- 14. Параллелограммы, из которых составлен параллелепипед, называются гранями,
- 15. Две грани параллелепипеда, имеющие общее ребро, называются
- 16. Свойства параллелепипеда.Противоположные грани параллелепипеда параллельны и равны.1.1
- 17. Назовите грани параллелепипедаНазовите рёбраНазовите смежные и противоположные граниНазовите основание и боковые грани параллелепипедаADCBA1D1C1B1
- 18. Задачи на построение сечения в параллелепипеде.Секущей плоскостью
- 19. Задача:На рёбрах параллелепипеда даны три точки A, B и C. Построить сечение параллелепипеда плоскостью ABC.
- 20. ABCДано: параллелепипед, точки
- 21. ABCРешение:Построим прямую, по которой секущая плоскость Пересекается
Многоугольник – часть плоскости, ограниченная линией, включая её саму. Что такое многоугольник?
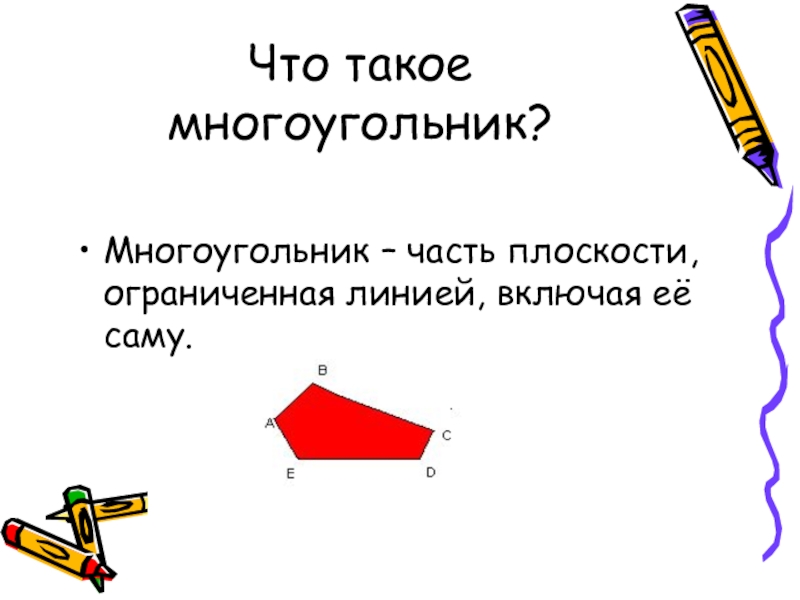
Слайд 2Многоугольник – часть плоскости, ограниченная линией, включая её саму.
Что такое многоугольник?
Слайд 3Тетраэдр.
Рассмотрим произвольный треугольник АBC и точку D, не лежащую в плоскости
этого треугольника.
A
B
C
D
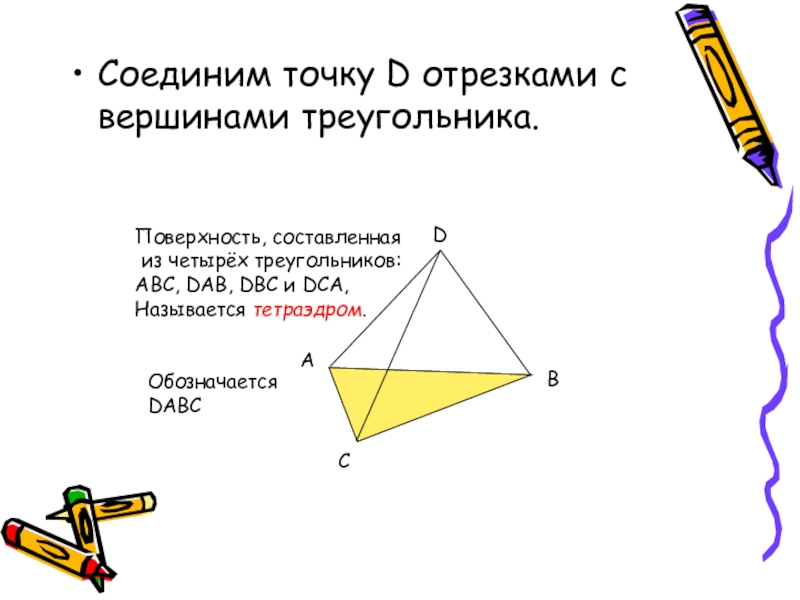
Слайд 4Соединим точку D отрезками с вершинами треугольника.
A
B
C
D
Поверхность, составленная
из четырёх треугольников:
ABC,
DAB, DBC и DCA,
Называется тетраэдром.
Называется тетраэдром.
Обозначается
DABC
Слайд 5Треугольники, из которых состоит тетраэдр, называются гранями, их стороны – рёбрами,
а вершины – вершинами тетраэдра.
У тетраэдра: 4 грани, 6 рёбер и 4 вершины.
Иногда выделяют одну из граней тетраэдра и называют её основанием, а три другие – боковыми гранями.
У тетраэдра: 4 грани, 6 рёбер и 4 вершины.
Иногда выделяют одну из граней тетраэдра и называют её основанием, а три другие – боковыми гранями.
Слайд 6
D
B
C
A
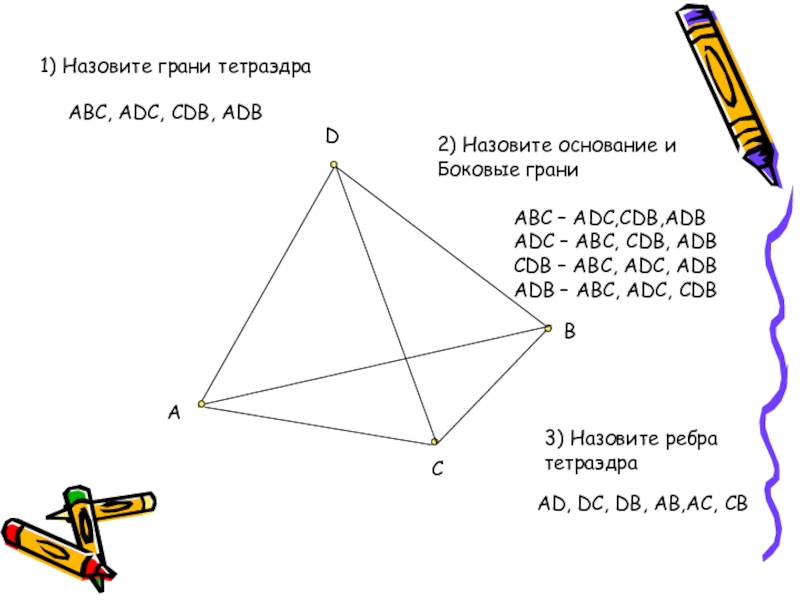
1) Назовите грани тетраэдра
ABC, ADC, CDB, ADB
2) Назовите основание и
Боковые
грани
ABC – ADC,CDB,ADB
ADC – ABC, CDB, ADB
CDB – ABC, ADC, ADB
ADB – ABC, ADC, CDB
3) Назовите ребра
тетраэдра
AD, DC, DB, AB,AC, CB
Слайд 7Задачи на построение сечения в тетраэдре.
Секущей плоскостью тетраэдра называется любая плоскость
по обе стороны от которой имеются точки данного тетраэдра.
Секущая плоскость пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра.
Сечением тетраэдра может быть треугольник и четырёхугольник.
Секущая плоскость пересекает грани тетраэдра по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением тетраэдра.
Сечением тетраэдра может быть треугольник и четырёхугольник.
Слайд 8Обязательные условия для задач на построение сечений.
Отрезок соединяющий две точки сечения,
лежит в одной плоскости (принадлежит одной грани).
Все дополнительные точки лежат на линии пересечения плоскостей.
Если строим плоскость параллельную данной, то секущая плоскость пересекает плоскость по прямым параллельным данной плоскости.
Все дополнительные точки лежат на линии пересечения плоскостей.
Если строим плоскость параллельную данной, то секущая плоскость пересекает плоскость по прямым параллельным данной плоскости.
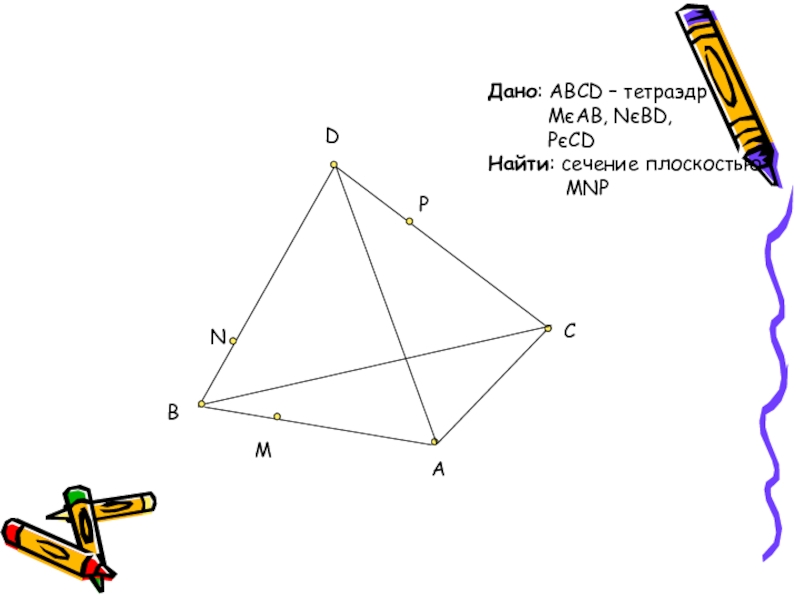
Слайд 9Задача:
На рёбрах AB, BD и CD тетраэдра ABCD отмечены точки M,
N и P. Построить сечение тетраэдра плоскостью MNP.
Слайд 11
D
C
A
B
M
N
P
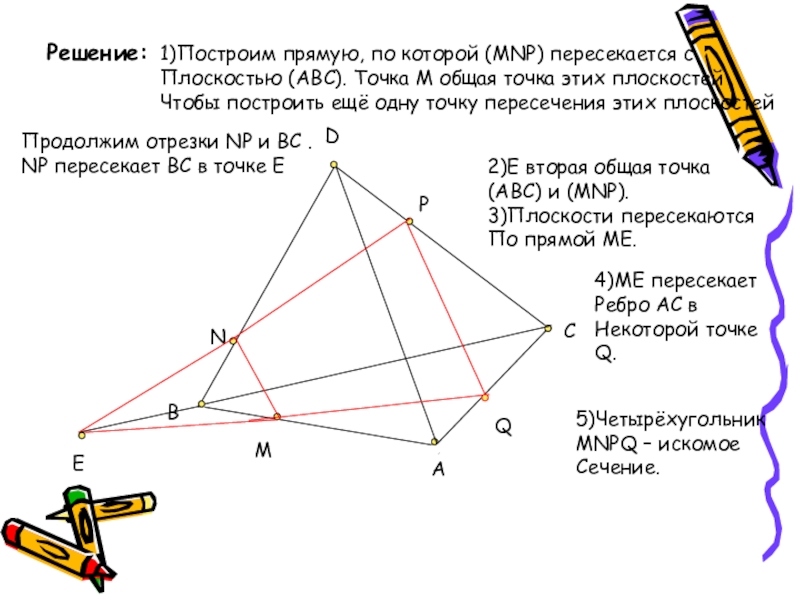
Решение:
1)Построим прямую, по которой (MNP) пересекается с
Плоскостью (ABC). Точка M
общая точка этих плоскостей
Чтобы построить ещё одну точку пересечения этих плоскостей
Чтобы построить ещё одну точку пересечения этих плоскостей
Продолжим отрезки NP и BC .
NP пересекает BC в точке E
E
2)E вторая общая точка
(ABC) и (MNP).
3)Плоскости пересекаются
По прямой ME.
4)ME пересекает
Ребро AC в
Некоторой точке
Q.
Q
5)Четырёхугольник
MNPQ – искомое
Сечение.
Слайд 12Параллелепипед.
Рассмотрим два равных параллелограмма ABCD и A1B1C1D1
Расположенных в параллельных плоскостях, так
что отрезки AA1, BB1, CC1, DD1 параллельны. Четырёхугольники ABB1A1, BCC1B1, CDD1C1, DAA1D1 – параллелограммы, т.к. каждый из них имеет попарно параллельные противоположные стороны.
Слайд 13
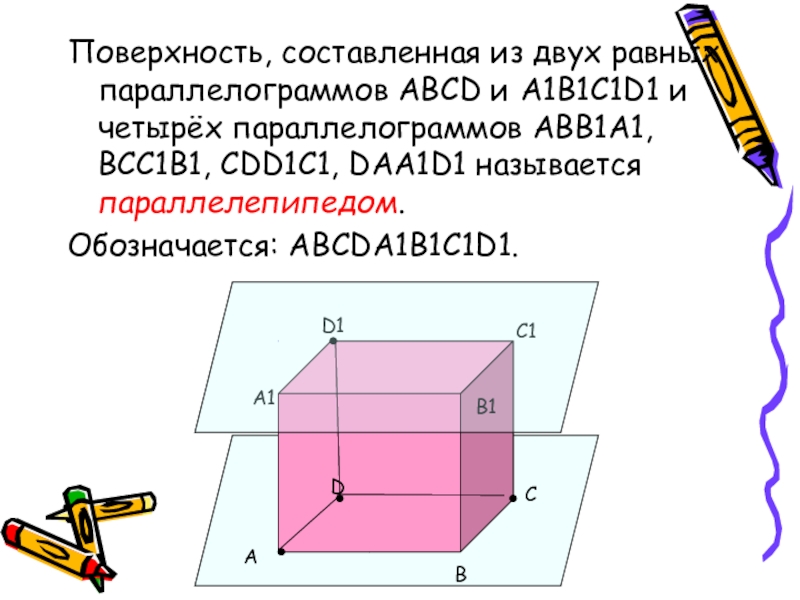
Поверхность, составленная из двух равных параллелограммов ABCD и A1B1C1D1 и четырёх
параллелограммов ABB1A1, BCC1B1, CDD1C1, DAA1D1 называется параллелепипедом.
Обозначается: ABCDA1B1C1D1.
Обозначается: ABCDA1B1C1D1.
A
D
C
B
A1
D1
C1
B1
Слайд 14Параллелограммы, из которых составлен параллелепипед, называются гранями, их стороны – рёбрами,
а вершины параллелограммов – вершинами параллелепипеда.
Параллелепипед имеет 6 граней, 12 рёбер, 8 вершин.
Параллелепипед имеет 6 граней, 12 рёбер, 8 вершин.
Слайд 15Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие
общих рёбер – противоположными.
Две вершины, не принадлежащие одной грани называются противоположными.
Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда.
Две противоположные грани называют основаниями, а остальные грани – боковыми гранями параллелепипеда.
Две вершины, не принадлежащие одной грани называются противоположными.
Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда.
Две противоположные грани называют основаниями, а остальные грани – боковыми гранями параллелепипеда.
Слайд 16Свойства параллелепипеда.
Противоположные грани параллелепипеда параллельны и равны.
1.1 Две грани параллелепипеда называются
параллельными, если их плоскости параллельны.
2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
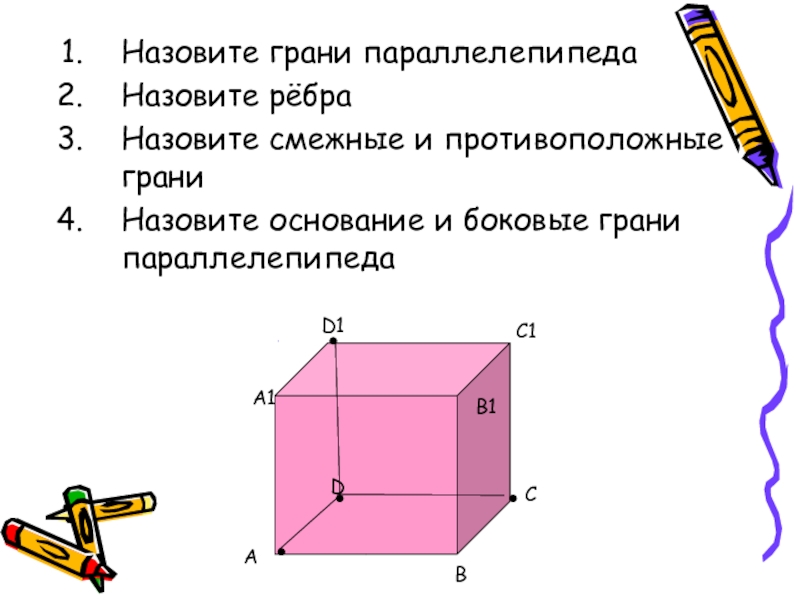
Слайд 17Назовите грани параллелепипеда
Назовите рёбра
Назовите смежные и противоположные грани
Назовите основание и боковые
грани параллелепипеда
A
D
C
B
A1
D1
C1
B1
Слайд 18Задачи на построение сечения в параллелепипеде.
Секущей плоскостью параллелепипеда называется любая плоскость
по обе стороны от которой имеются точки данного параллелепипеда.
Секущая плоскость пересекает грани параллелепипеда по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением параллелепипеда.
Сечением параллелепипеда могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники.
Секущая плоскость пересекает грани параллелепипеда по отрезкам. Многоугольник, сторонами которого являются эти отрезки, называется сечением параллелепипеда.
Сечением параллелепипеда могут быть треугольники, четырёхугольники, пятиугольники и шестиугольники.
Слайд 19Задача:
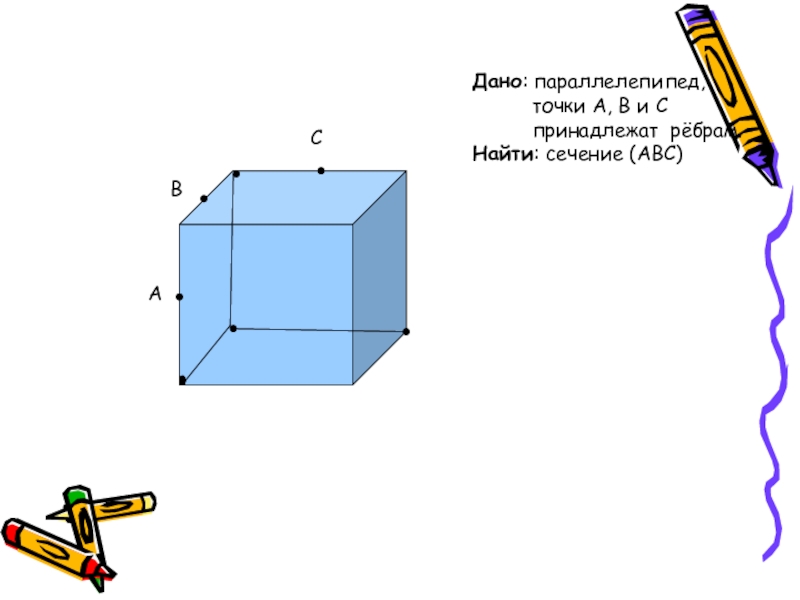
На рёбрах параллелепипеда даны три точки A, B и C. Построить
сечение параллелепипеда плоскостью ABC.
Слайд 21
A
B
C
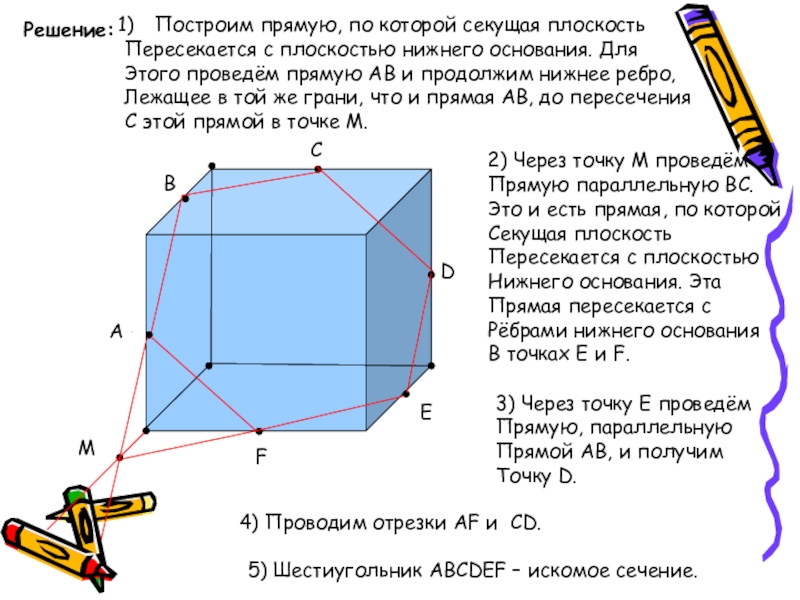
Решение:
Построим прямую, по которой секущая плоскость
Пересекается с плоскостью нижнего основания.
Для
Этого проведём прямую AB и продолжим нижнее ребро,
Лежащее в той же грани, что и прямая AB, до пересечения
С этой прямой в точке M.
Этого проведём прямую AB и продолжим нижнее ребро,
Лежащее в той же грани, что и прямая AB, до пересечения
С этой прямой в точке M.
2) Через точку M проведём
Прямую параллельную BC.
Это и есть прямая, по которой
Секущая плоскость
Пересекается с плоскостью
Нижнего основания. Эта
Прямая пересекается с
Рёбрами нижнего основания
В точках E и F.
M
F
E
3) Через точку E проведём
Прямую, параллельную
Прямой AB, и получим
Точку D.
D
4) Проводим отрезки AF и CD.
5) Шестиугольник ABCDEF – искомое сечение.
