- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теорема Пифагора (8 класс)
Содержание
- 1. Презентация по математике на тему Теорема Пифагора (8 класс)
- 2. Теорема Пифагора
- 3. DCНазовите прямоугольный треугольник
- 4. ABCСвойства прямоугольного треугольника.
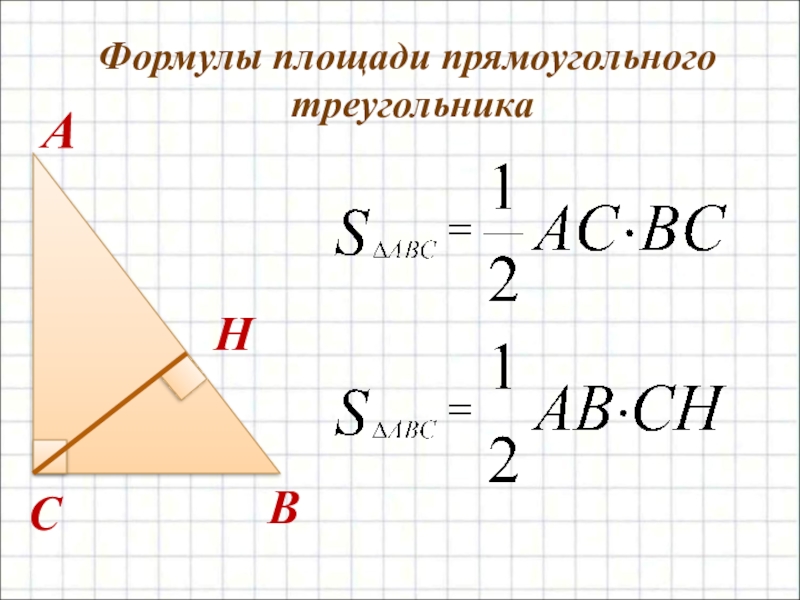
- 5. Формулы площади прямоугольного треугольникаBCAH
- 6. Историческая справка Египетские строители и
- 7. Историческая справка.
- 8. Задачи на чертежах
- 9. Доказать: PNMK - квадрат1
- 10. Найти: 2
- 11. ABC30ºD45ºНайти: 23
- 12. Дано: -равнобедренныйAB=BC=17см, АС=16 см, BD- высотаНайти: В4
- 13. Теорема ПифагораГеометрическая формулировка теоремы ПифагораПлощадь квадрата, построенного
- 14. ПИФАГОР САМОССКИЙ
- 15. Теорема Пифагора ПИФАГОР
- 16. 1) Площадь квадрата со стороной
- 17. 2) Площадь квадрата, составленного из четырех равных
- 18. ПИФАГОР САМОССКИЙ
- 19. Задачи на чертежах
- 20. А8СВ6?45DCE?1
- 21. ВАСNMKP17H?АС=162
- 22. Дано: -равнобедренныйAB=BC=17см, АС=16 см, BD- высотаНайти: В3
- 23. Дано: АВСВH -высотаHАH=9, HC=16BC=20Найти: АВ4
- 24. Дано:ABCD-трапецияАС=СD, АВ=3, CD=5Найти:AD 5
- 25. О теореме Пифагора.Суть истины вся в том,
Слайд 6 Историческая справка
Египетские строители и землемеры для определения
прямого
простую веревку длиной, например, 12 метров,
которая специальными петлями или узлами была
разделена на 3, 4 и 5 метров. Для определения прямого
угла на земле землемер натягивал одну из частей
веревки, например, 3 метра, и с помощью 2
специальных колышек фиксировал ее на земле.
Затем веревку натягивали с помощью третьей петли,
и эта петля фиксировалась колышком. Угол,
образованный между двумя меньшими
сторонами в точности равнялся 90 градусов.
Слайд 13Теорема Пифагора
Геометрическая формулировка теоремы Пифагора
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника,
ПИФАГОР САМОССКИЙ
(ок.580 – 500 г до н.э.)
c²=a²+b²
Слайд 14 ПИФАГОР САМОССКИЙ
Теорема Пифагора
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
Слайд 161) Площадь квадрата со стороной
ПИФАГОР
(ок.580 – 500 г до н.э.)
Теорема Пифагора
равна
Слайд 172) Площадь квадрата, составленного из четырех равных
прямоугольных треугольников и квадрата
равна:
ПИФАГОР САМОССКИЙ
(ок.580 – 500 г до н.э.)
Теорема Пифагора
Слайд 25О теореме Пифагора.
Суть истины вся в том, что нам она –
Когда хоть раз в прозрении её увидим свет,
И теорема Пифагора через столько лет
Для нас, как для него, бесспорна, безупречна…
А.Шамиссо
ПИФАГОР САМОССКИЙ
(ок.580 – 500 г до н.э.)