- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад по математике на тему Теорема Пифагора (9 класс)
Содержание
- 1. Презентация по математике на тему Теорема Пифагора (9 класс)
- 2. Руководитель проекта:
- 3. Цель проекта: Показать применение теоремы Пифагора в практической деятельности людей.
- 4. Гипотеза: Теорема Пифагора открывает путь с
- 5. Задачи проекта: Получить информацию по данному вопросу
- 6. Методы работы Изучение различных источников:
- 7. По данным интернет-опросов Теорема Пифагора
- 8. Опрос общественного мненияВывод: Данные, полученные при опросе, во многом совпадают с данными Интернет – опросов.
- 9. Во времена Пифагора : « Площадь квадрата,
- 10. Доказательства теоремы Существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.).
- 11. Самое простое доказательствоДано: прямоугольный треугольник, a,b - катеты, с – гипотенузаДоказать: Доказательство:
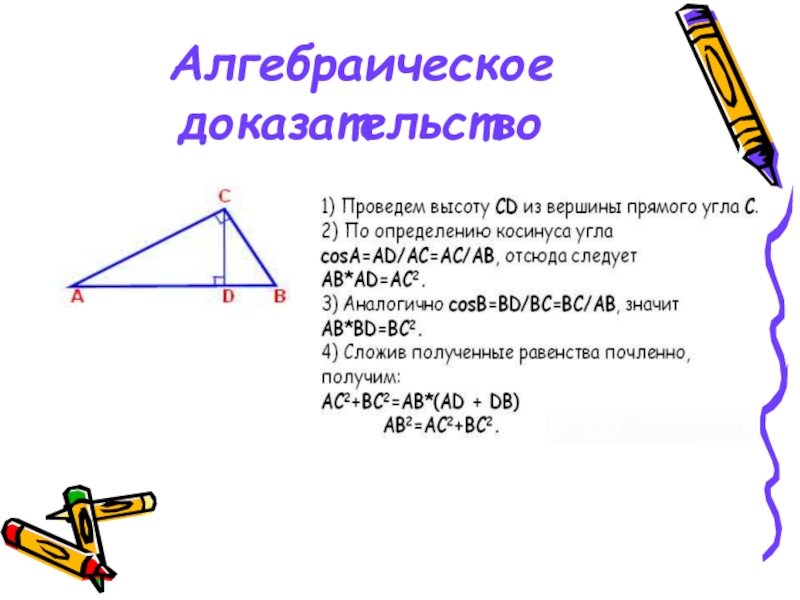
- 12. Алгебраическое доказательство
- 13. Геометрическое доказательство
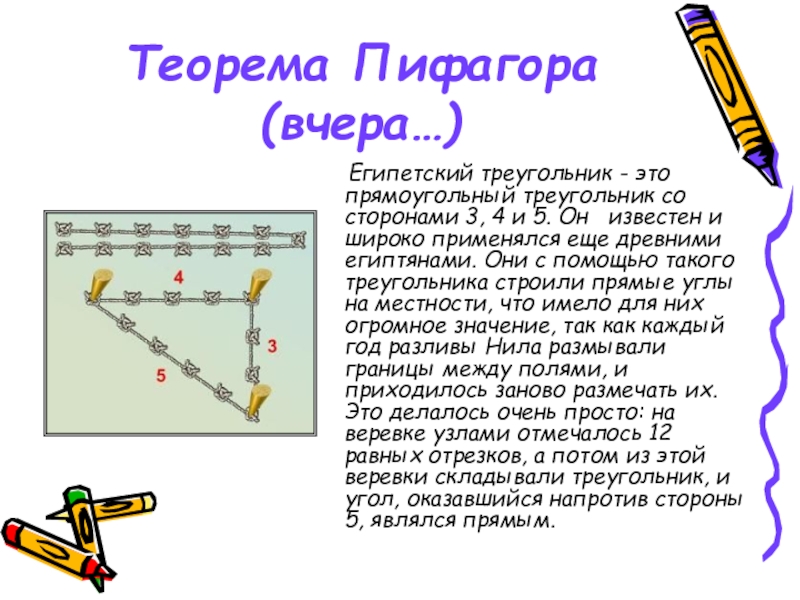
- 14. Теорема Пифагора (вчера…) Египетский треугольник
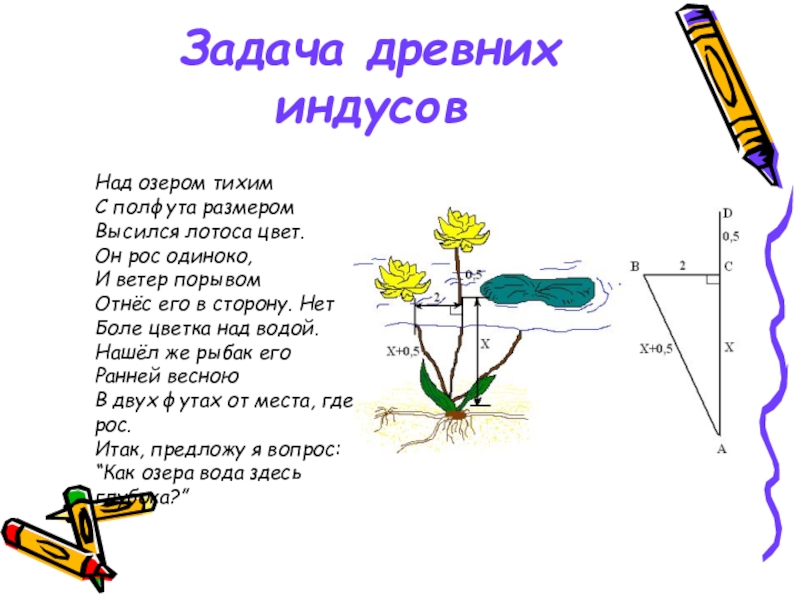
- 15. Задача древних индусовНад
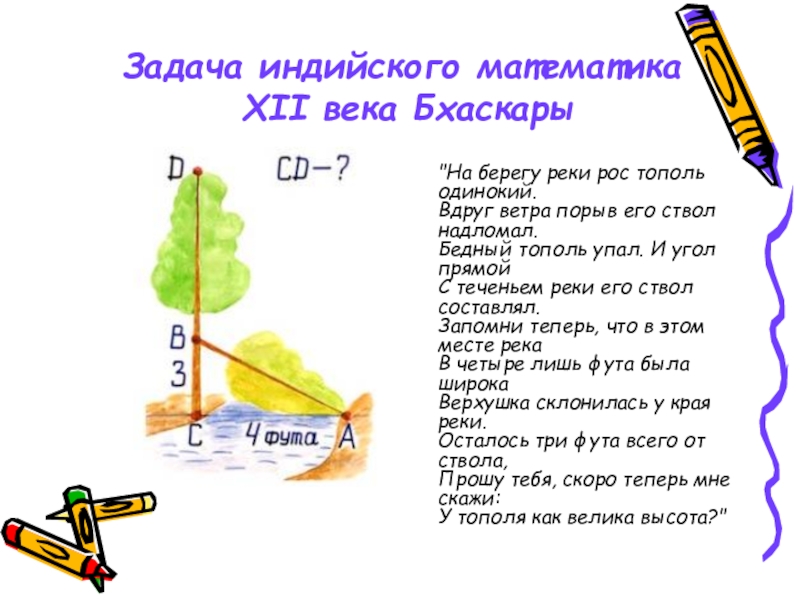
- 16. "На берегу реки рос
- 17. Задача о бамбуке из древнекитайского трактата "Гоу-гу"
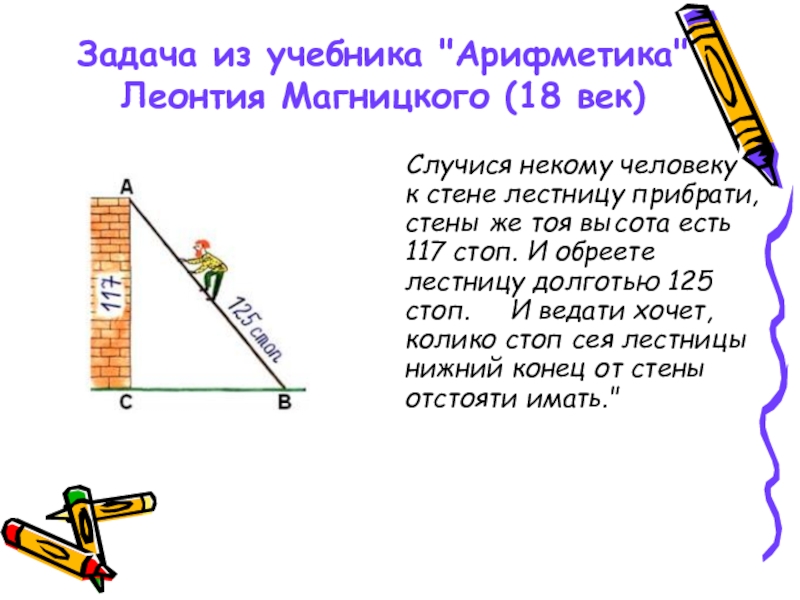
- 18. Задача из учебника "Арифметика" Леонтия Магницкого (18
- 19. Теорема Пифагора (сегодня, завтра…) При строительстве
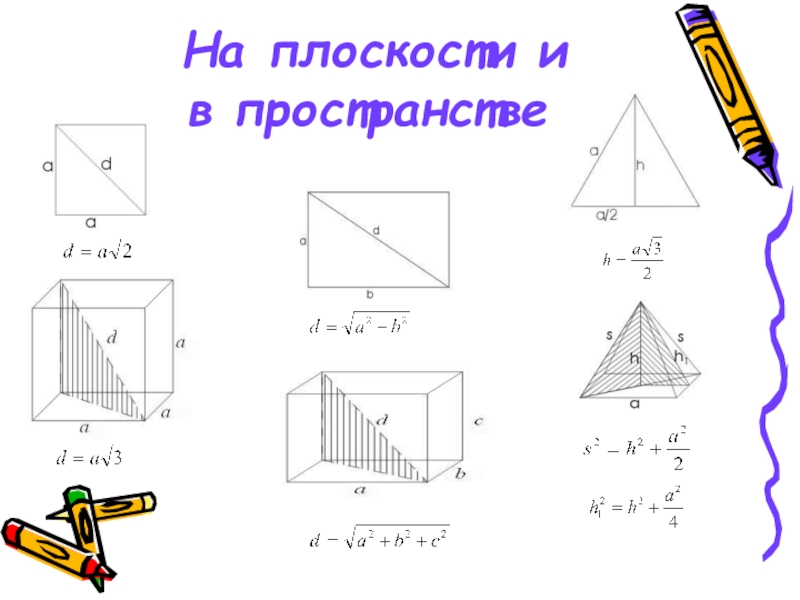
- 20. На плоскости и в пространстве
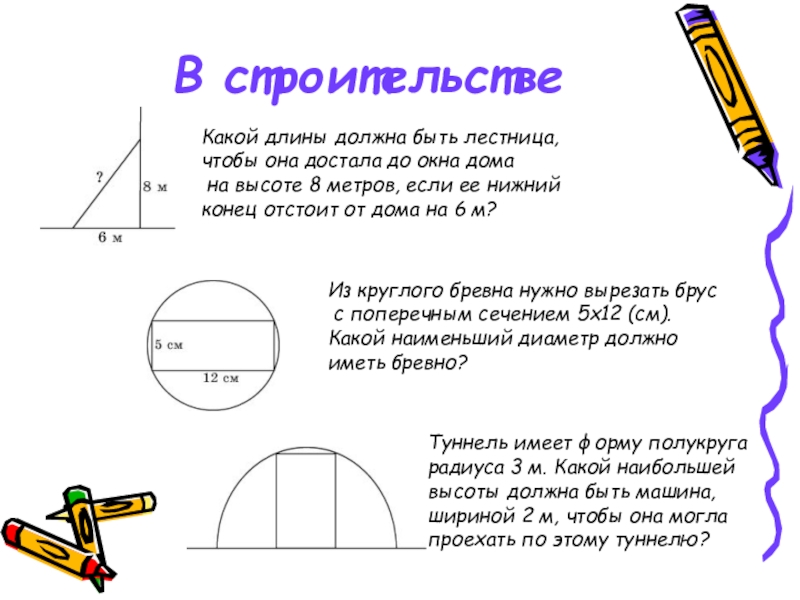
- 21. В строительствеКакой длины должна быть лестница, чтобы
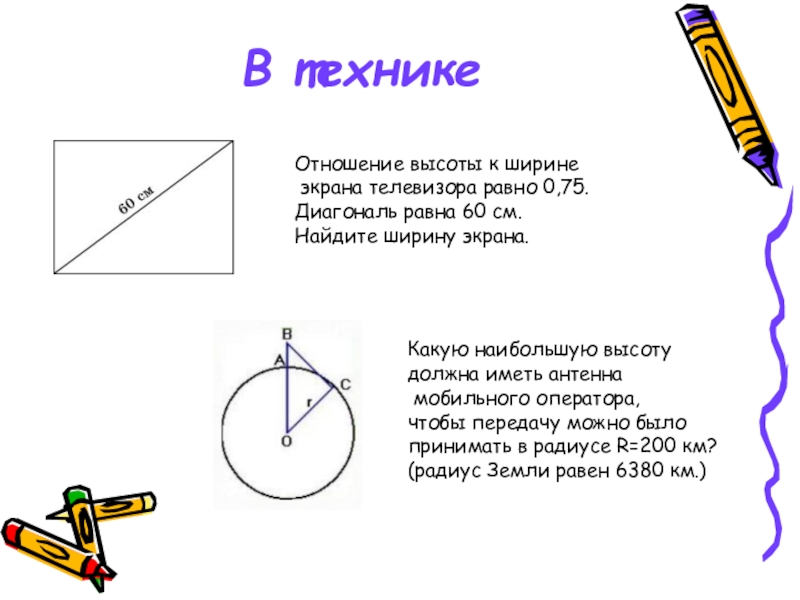
- 22. В техникеОтношение высоты к ширине экрана телевизора
- 23. В навигацииДва парохода вышли из порта, следуя
- 24. Многомерные пространства Существуют кинотеатры где показывают
- 25. Значение теоремы Пифагора Теорема Пифагора имеет
- 26. Послание внеземным цивилизациям
- 27. Пребудет вечной истина, как скороЕё познает слабый
Слайд 1ПРОЕКТ
ТЕОРЕМА ПИФАГОРА
(вчера, сегодня, завтра…)
«Геометрия владеет
двумя сокровищами:
одно из них
это теорема Пифагора»
Иоганн Кеплер
Слайд 4Гипотеза:
Теорема Пифагора открывает путь с прямой на плоскость, с
Слайд 5Задачи проекта:
Получить информацию по данному вопросу из разных источников;
Проанализировать информацию;
Рассмотреть
Показать применение теоремы Пифагора
Оформить результаты работы в виде презентации;
Сделать выводы.
Слайд 6Методы работы
Изучение различных источников:
книги, статьи, материалы в интернете;
Опрос учащихся и учителей школы;
Отбор необходимой информации;
Компьютерное моделирование.
Слайд 7По данным
интернет-опросов
Теорема Пифагора самая известная теорема геометрии,
Слайд 8Опрос общественного мнения
Вывод: Данные, полученные при опросе, во многом совпадают с
Слайд 9Во времена Пифагора :
« Площадь квадрата, построенного на гипотенузе прямоугольного
Современная формулировка:
« В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов».
Формулировка теоремы
Слайд 10Доказательства теоремы
Существует около 500 различных доказательств этой теоремы (геометрических,
Слайд 11Самое простое доказательство
Дано: прямоугольный треугольник,
a,b - катеты,
Доказать:
Доказательство:
Слайд 14Теорема Пифагора (вчера…)
Египетский треугольник - это прямоугольный треугольник
Слайд 15
Задача древних индусов
Над озером тихим
С полфута размером
Высился
Слайд 16 "На берегу реки рос тополь одинокий. Вдруг ветра порыв
Задача индийского математика
XII века Бхаскары
Слайд 17Задача о бамбуке из древнекитайского трактата "Гоу-гу"
Имеется бамбук
Слайд 18Задача из учебника "Арифметика" Леонтия Магницкого (18 век)
Случися некому
Слайд 19Теорема Пифагора (сегодня, завтра…)
При строительстве любого сооружения, рассчитывают расстояния,
Теорема Пифагора применяется практически во всех современных технологиях, а также открывает простор для создания и придумывания новых.
Слайд 21В строительстве
Какой длины должна быть лестница,
чтобы она достала до окна
на высоте 8 метров, если ее нижний конец отстоит от дома на 6 м?
Из круглого бревна нужно вырезать брус
с поперечным сечением 5х12 (см).
Какой наименьший диаметр должно
иметь бревно?
Туннель имеет форму полукруга
радиуса 3 м. Какой наибольшей
высоты должна быть машина,
шириной 2 м, чтобы она могла
проехать по этому туннелю?
Слайд 22В технике
Отношение высоты к ширине
экрана телевизора равно 0,75.
Диагональ равна
Найдите ширину экрана.
Какую наибольшую высоту
должна иметь антенна
мобильного оператора,
чтобы передачу можно было
принимать в радиусе R=200 км?
(радиус Земли равен 6380 км.)
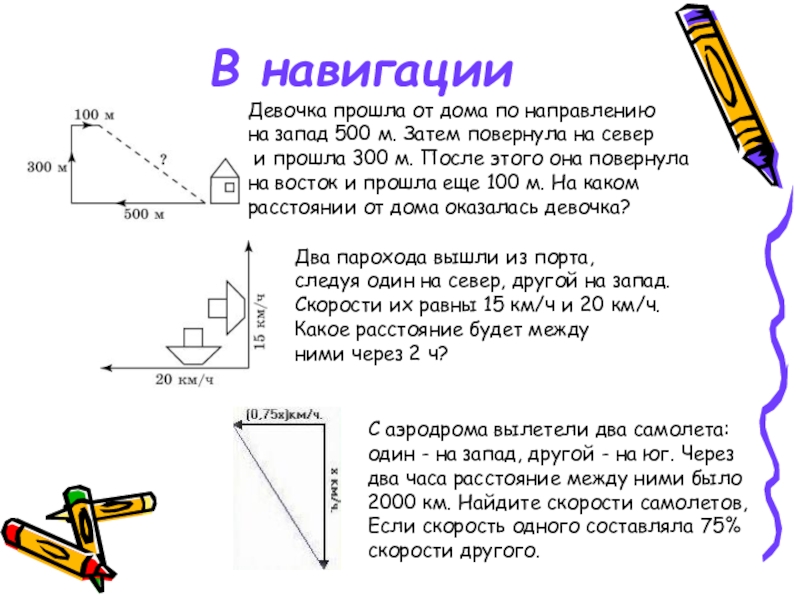
Слайд 23В навигации
Два парохода вышли из порта,
следуя один на север, другой
Скорости их равны 15 км/ч и 20 км/ч.
Какое расстояние будет между
ними через 2 ч?
Девочка прошла от дома по направлению
на запад 500 м. Затем повернула на север
и прошла 300 м. После этого она повернула
на восток и прошла еще 100 м. На каком
расстоянии от дома оказалась девочка?
С аэродрома вылетели два самолета:
один - на запад, другой - на юг. Через
два часа расстояние между ними было
2000 км. Найдите скорости самолетов,
Если скорость одного составляла 75%
скорости другого.